16. Основные предпосылки регрессионного анализа (условия Гаусса-Маркова)
1 0. В моделиY = aX + b + e, (2.4)
где a, b – теоретические параметры (теоретические коэффициенты)
регрессии, e – случайное возмущение.парной линейной регрессии возмущение e есть случайная величина, объясняющая переменная X – величина неслучайная.
2 0. Математическое ожидание случайного возмущения e i равно нулю:
M (e i) = 0 для всех наблюдений 1 ).
Данное условие означает, что хотя в каждом конкретном наблюдении случайное отклонение может быть положительным или отрицательным, оно не должно иметь систематического смещения. Другими словами, случайное возмущение в среднем не должно оказывать влияния на результирующую переменную.
3 0. Дисперсия случайных возмущений постоянна:
D (e i) = s 2 для всех наблюдений.
Выполнение данного условия называется гомоскедастичностью (постоянством дисперсии) возмущений, невыполнение – гетероскедастичностью (непостоянством дисперсии) возмущений.
4 0. Возмущения e i и e j (i ¹ j) не коррелированны:
cov (e i , e j) = 0 для всех наблюдений.
Если данное условие выполняется, то говорят об отсутствии автокорреляции возмущений, в противном случае – о ее наличии.
5 0. Возмущение e i есть нормально распределенная случайная величина:
e i ~ N (0, s) для всех наблюдений.
Условия Гаусса-Маркова:
1. 
– условие, гарантирующее несмещённость оценок МНК.
2. 
– условие гомоскедастичности, его нарушение приводит к проблеме гетероскедастичности.
3. 
– условие отсутствия автокорреляции предполагает отсутствие систематической связи между значениями случайного члена в любых двух наблюдениях. Если данное условие не выполняется, то в модели возникает проблема автокорреляции случайных возмущений.
|
|
4. 
для всех 
условие независимости случайного возмущения и объясняющей переменной. Значение любой независимой переменной в каждом наблюдении должно считаться экзогенным, полностью определяемым внешними причинами, не учитываемыми в уравнении регрессии.
Достаточно часто накладывают ещё одно условие на остатки модели, но данное условие не является условием Гаусса-Маркова: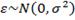 
, оно очень полезно для проверки многих гипотез.
17. Нелинейная регрессия. Виды нелинейной регрессии
Нелинейная регрессия – регрессионная модель зависимости результативной переменной от одной или нескольких объясняющих переменных, выражаемая в виде нелинейной функции.
Все нелинейные модели регрессии могут быть разделены, как и линейные модели, на парные и множественные. По целям и решаемым задачам нелинейная регрессия аналогичная классической линейной регрессией. Отличие только в форме связи и методах оценки параметров.
Выбор формы связи нелинейной зависимости осуществляется по следующим критериями:
· исходя из содержательного анализа исследуемого явления;
· на основе результатов анализа взаимосвязи между переменными, например, с помощью графического метода.
Для оценки параметров нелинейных регрессий могут использоваться два подхода:
· линеаризация уравнения с помощью подходящих преобразований и оценка его параметров с помощью метода наименьших квадратов;
· оценка параметров на основе метода максимального правдоподобия и применение итеративных процедур методов оптимизации.
Различают два класса нелинейных регрессий:
|
|
· относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам;
· по оцениваемым параметрам.
Рассмотрим нелинейные регрессии по включаемым в нее объясняющим переменным, но линейные по оцениваемым параметрам.
Данный класс нелинейных регрессий включает уравнения, в которых у линейно связан с параметрами. Примером могут служить следующие функции.
1. Полиномы разных степеней. Например, полином k -й степени 
.
2. Равносторонняя гипербола – 
.
Регрессии нелинейные по оцениваемым параметрам. К данному классу регрессий относятся уравнения, в которых у нелинейно связан с параметрами. Примером таких нелинейных регрессий являются функции:
· степенная – 
;
· показательная – 
;
· экспоненциальная – 
.
Данный класс нелинейных моделей подразделяется на два типа:
1) нелинейные модели внутренне линейные;
2) нелинейные модели внутренне нелинейные.
18. Общая модель множественной линейной регрессии. Основные предположения регрессионного анализа(условия Гаусса-Маркова, условие нормальности распределения случайной ошибки, условие линейной независимости объясняющих переменных)
Построение модели множественной регрессии является одним из методов характеристики аналитической формы связи между зависимой (результативной) переменной и несколькими независимыми (факторными) переменными.Модель множественной регрессии строится в том случае, если коэффициент множественной корреляции показал наличие связи между исследуемыми переменными.
Общий вид линейной модели множественной регрессии:
|
|
)
где Yi – значение результативной переменной,
Х1i…Хki – значения факторных переменных;
β1…βk – неизвестные коэффициенты модели множественной регрессии;
ui – случайные ошибки модели множественной регрессии.
Основные предположения регрессионного анализа относятся к случайной компоненте и имеют решающее значение для правильного и обоснованного применения регрессионного анализа в эконометрических исследованиях.
В классической модели регрессионного анализа предполагаются выполненными следующие предпосылки (условия Гаусса-Маркова):
1. Величины являются случайными.
.2. Математическое ожидание возмущений равно нулю:.
3. Возмущения и некоррелированы:,.
4.Дисперсия возмущения одна и та же для каждого наблюдения:. Это условие одинаковости дисперсий возмущений называется условием гомоскедастичности. Нарушение этого условия называется гетероскедастичностью.
5. Величины взаимно независимы со всеми значениями объясняющих переменных. Обычно считают, что объясняющие переменные являются неслучайными величинами.
Эти предпосылки образуют первую группу предпосылок, необходимых для проведения регрессионного анализа в рамках классической модели.
Вторая группа предпосылок дает достаточные условия для обоснованного проведения проверки статистической значимости эмпирических регрессий:
6. Совместное распределение случайных величин является нормальным.
19.Вывод формул для оценок коэффициентов модели множественной регрессии. Основные предпосылки регрессионного анализа (условие Гаусса-Маркова) по МНК. Матричная запись основных формул для множественной регрессии. Теорема Гаусса-Маркова.
Доказано, что для получения по МНК наилучших результатов (при этом оценки bi обладают свойствами состоятельности, несмещенности и эффективности) необходимо выполнение ряда предпосылок относительно случайного отклонения