Все зависимости между экономическими переменными можно разделить на 2 вида˸
1. Функциональные. В случае если каждому значению независимой переменной или нескольким независимых переменных соответствует одно строго определенное значение зависимой переменной, то такая зависимость принято называть функциональной. В ней отсутствует воздействие случайных факторов, в связи с этим в экономике функциональная зависимость встречается редко.
2. Статистические (Стахостические, Вероятностные). В экономике каждому значению независимых переменных может соответствовать несколько значений зависимой переменной исходя из воздействия неучтенных и случайных факторов. (Примером статистической связи является зависимость урожайности от количества внесенных удобрений, производительности труда на предприятии от его энерговооруженности и т.п.)
Зависимость между переменными, на которую накладывается воздействие случайных факторов, принято называть статистической. Стоит сказать, что для нее характерно то, что изменение независимой переменной приводит к изменению математического ожидания зависимой переменной. Уравнение регрессии – математическая формула, описывающая статистическую зависимость между переменными. В случае если формула описывается линейной функцией, то регрессия принято называть линейной. В случае если нелинейной функцией – нелинейной регрессией. В случае если регрессия связывает одну зависимую и одну независимую переменную, то такая регрессия принято называть парной (простой). В случае если рассматривается зависимость экономической переменной от нескольких экономических переменных, то такая регрессия принято называть множественной.
Корреляционной связью называют частный случай статистической связи, состоящий в том, что разным значениям одной переменной соответствуют различные средние значения другой. С изменением значения х закономерным образом изменяется среднее значение у, в то время как в каждом отдельном случае у может принимать множество различных значений (с различными вероятностями).
Простейшей системой корреляционной связи является линейная связь между двумя признаками – парная линейная корреляция, уравнение которой называется уравнением парной регрессии: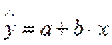 
.
Способы оценивания и оценки различных характеристик.
Свойства оценок.
1. Постановочный способ – определение конечных целей моделирования, набора участвующих в модели факторов и показателей, их роли;
2. априорный – предмодельныйанализ экономической сущности изучаемого явления, формирование и формализация априорной информации, в частности, относящейся к природе и генезису исходных статистических данных и случайных остаточных составляющих;
3. параметризации – собственно моделирование, т.е. выбор общего вида модели, в том числе состава и формы входящих в нее связей;
4. информационный – сбор необходимой статистической информации, т.е. регистрация значений участвующих в модели факторов и показателей на различных временных или пространственных тактах функционирования изучаемого явления;
5. идентификация модели – статистический анализ модели и в первую очередь статистическое оценивание неизвестных параметров модели;
6. верификация модели – сопоставление реальных и модельных данных, проверка адекватности модели, оценка точности модельныхданных.
Свойства:
Свойства оценок, полученных с помощью МНК:
1. Линейность оценок – оценки параметров 
и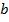 
представляют собой линейные комбинации наблюдаемых значений объясняемой переменной 
.
2. Несмещённость оценок - если её выборочное математическое ожидание равно оцениваемому параметру генеральной совокупности
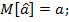
3. Состоятельность оценок - это точечная оценка, сходящаяся по вероятности к оцениваемому параметру.
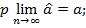
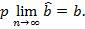
4. Эффективность – данное свойство означает, что оценка имеет минимальную дисперсию в заданном классе оценок:
