Автокорреляция – статистическая взаимосвязь между последовательностями величин одного ряда, взятыми со сдвигом, например, для случайного процесса – со сдвигом по времени.
Наличие автокорреляции случайных ошибок регрессионной модели приводит к ухудшению качества МНК-оценок параметров регрессии, а также к завышению тестовых статистик, по которым проверяется качество модели (то есть создается искусственное улучшение качества модели относительно ее действительного уровня точности).
Автокорреляционная функция – это функция, описывающая зависимость коэффициентов автокорреляции от лага.


где
 – количество наблюдений;
– количество наблюдений;
 – значение i -го признака одного события;
– значение i -го признака одного события;
 – значение i -го признака другого события;
– значение i -го признака другого события;
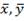 – средние значения
– средние значения  и
и  соответственно.
соответственно.
Сезонные составляющие временного ряда могут быть найдены с помощью коррелограммы. Коррелограмма показывает коэффициенты автокорреляции для последовательности лагов из определенного диапазона. На коррелограмме обычно отмечается диапазон в размере двух стандартных ошибок на каждом лаге, однако обычно величина автокорреляции более интересна, чем ее надежность, потому что интерес в основном представляют очень сильные (а, следовательно, высоко значимые) автокорреляции.

Для временного ряда, содержащего тренд, с ростом значения лага  коррелограмма не стремится к нулю. Для временного ряда с сезонными колебаниями коррелограмма будет содержать периодические всплески, соответствующие периоду сезонных колебаний. Данный факт позволяет устанавливать предполагаемый период сезонности.
коррелограмма не стремится к нулю. Для временного ряда с сезонными колебаниями коррелограмма будет содержать периодические всплески, соответствующие периоду сезонных колебаний. Данный факт позволяет устанавливать предполагаемый период сезонности.
Другой метод исследования периодичности состоит в исследовании частной автокорреляционной функции (ЧАКФ), представляющей собой углубление понятия обычной автокорреляционной функции. Частная автокорреляционная функция показывает корреляцию между двумя случайными переменными за вычетом влияния всех внутренних значений автокорреляции. В частной автокорреляционной функции устраняется зависимость между наблюдениями внутри лага (промежуточными наблюдениями). Частная автокорреляция на данном лаге аналогична обычной автокорреляции, за исключением того, что при вычислении из неё исключается влияние автокорреляций с меньшими лагами.
На лаге 1 (когда нет промежуточных элементов внутри лага), частная автокорреляция равна обычной автокорреляции. На практике, частная автокорреляция даёт более «чистую» картину периодических зависимостей. Если значение ЧАКФ близко к 1 при первом лаге, то велика вероятность того, что существует проблема единичных корней.
Вид автокорреляционной функции и частной автокорреляционной функции зависит от длины рассматриваемого временного ряда. Если ряд достаточно длинный, формы автокорреляционных функций оказываются более чётко выраженными, модель ряда и параметры модели определяются достаточно чётко. Если же ряд короткий, то коррелограммы теряют свою чёткость, а идентификация становится более сложной, поскольку снижается точность вычислений автокорреляционной и частной автокорреляционной функций.
Можно построить две основные параметрические модели стационарных временных рядов, процесс авторегрессии и процесс скользящего среднего. Данные модели предполагают различные виды связи между текущим значением временного ряда  и предшествующими ему по времени значениями членов ряда.
и предшествующими ему по времени значениями членов ряда.