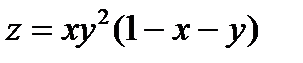Определить интервал сходимости ряда и исследовать сходимость на концах интервала.
1) Пример решения четвертого задания.
а)  ;
;
Для нахождения интервала сходимости, воспользуемся признаком Даламбера. Определим п +1 член ряда.
 , тогда
, тогда  .
.
По признаку Даламбера:
 =
=  =
=  =
=  =
=
=  =
=  так как
так как
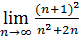 =
=  =
=
Если возникла неопределенность  , то числитель и знаменатель делим на наивысшую степень (
, то числитель и знаменатель делим на наивысшую степень (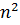 ).
).
= 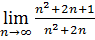 =
=  =
= 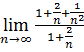 =
= 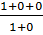 = 1
= 1
Ряд будет сходится если 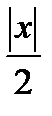 < 1 =>
< 1 => 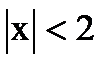 => -2 < x < 2.
=> -2 < x < 2.
В интервале (-2 < x < 2) ряд сходится абсолютно, вне интервала расходится. Проверим сходимость на границах.
Проверим левую границу x = -2. Подставим в исходный ряд вместо x левую границу -2.
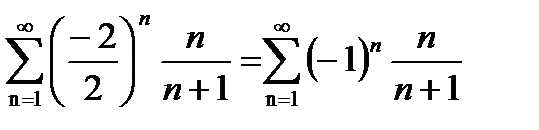 .
.
Т.к. ряд знакочередующийся, то проверим выполнение признака Лейбница.
1) 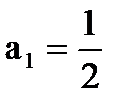 <
< 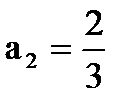 <
<  < …
< …
Первое условие признака выполнилось. Проверим второе.
2) 
Второе условие не выполнилось, следовательно, ряд при x = -2 расходится и -2 не входит в интервал сходимости.
Аналогично проверяем правую границу.
x = 2  .
.
Проверим выполнение необходимого признака сравнения

Так как предел не равен нулю, то необходимый признак сходимости не выполняется, ряд расходится и следовательно 2 не входит в интервал сходимости.
Т. о. интервал сходимости -2 < x < 2.
б)  .
.
По признаку Даламбера:

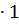 =
= 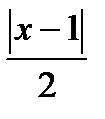
Ряд будет сходится если 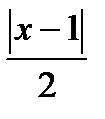 < 1 =>
< 1 =>  => -2 < x -1 < 2.
=> -2 < x -1 < 2.
-1 < x < 3.
Проверим левую границу x = -1  .
.
Т.к. ряд знакочередующийся, то проверим выполнение признака Лейбница.
1)  <
< 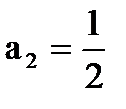 <
<  < …
< …
Первое условие признака выполнилось. Проверим второе.
2) 
Второе условие выполнилось, следовательно, ряд при x = -1 сходится и левая граница -1 входит в интервал сходимости.
Рассмотрим степенной ряд при x = 3. Имеем  .
.
Это гармонический ряд. Он расходится и, следовательно, 3 не входит в интервал сходимости.
Т. о. интервал сходимости -1 £ x < 3.
Задание 2. Пользуясь разложением в ряд Маклорена функций 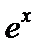 ,
, 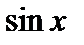 ,
,  ,
, 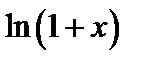 ,
,  ,
,  , разложить данные функции в ряд. Указать область сходимости.
, разложить данные функции в ряд. Указать область сходимости.
1.  . 2.
. 2.  .
.
3.  . 4.
. 4.  .
.
5. 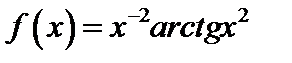 . 6.
. 6.  .
.
7.  8.
8.  .
.
9.  . 10.
. 10.  .
.
Образец решения задания 2.
а) Разложить функцию  в ряд Маклорена.
в ряд Маклорена.
cos t = 1 - 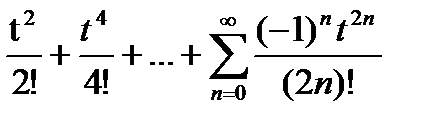 (см. приложение №4).
(см. приложение №4).
Заменим t на 
 (1 -
(1 - 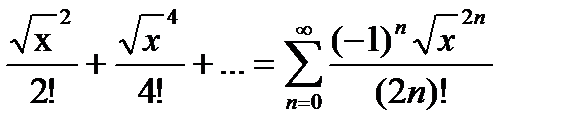 ) =
) =  =
= 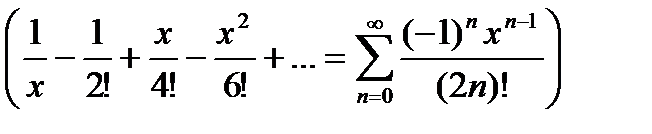 .
.
Определим радиус сходимости полученного рячда.
 , где 0 – бесконечно малая
, где 0 – бесконечно малая
 =>
=>  ; - ¥ < x < ¥. Т.е. интервал сходимости вся вещественная ось.
; - ¥ < x < ¥. Т.е. интервал сходимости вся вещественная ось.
Задание 3. Разложить данные функции в ряд Фурье в указанных интервалах.
1.  , (-2; 2) 6.
, (-2; 2) 6.  , (-π; π)
, (-π; π)
2.  , (-π; π) 7.
, (-π; π) 7.  , (-3; 3).
, (-3; 3).
3. f(x) =x -1 (-π; π) 8.  , (-π; π).
, (-π; π).
4. f(x) =x (-π; π) 9.  , (-3; 3).
, (-3; 3).
5. f (x) = x (-π; π) 10.  .
.
Образец решения задания 3.
Разложить данные функции в ряд Фурье в указанных интервалах.
f (x)= x +2, (-2;2)
Формула разложения в ряд Фурье имеет вид:
f (x) =  +
+ 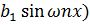 ,
,  ; x Î[ a; b]
; x Î[ a; b]
Функцию разложить в ряд Фурье можно, если она является кусочно-непрерывной и периодической. Чтобы функцию сделать периодической, ее продолжают периодическим образом с периодом Т на всю вещественную ось.
Разложение заданной функции в ряд имеет вид:
x +2 =  +
+  =
=
 +
+ 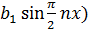 .
.
Найдем коэффициенты ряда Фурье.
a 0 =  ,
,
a 1 = 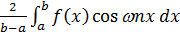 =
= 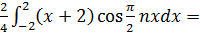
=  +
+ 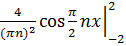 = 0+
= 0+  ,
,
b 1 = 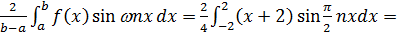
=  +
+  = - 4·
= - 4·  ·(-1)-0+0-0=
·(-1)-0+0-0=  .
.
Подставим найденные коэффициенты в формулу разложения, получим
x +2 = 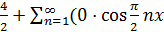 +
+ 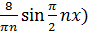 = 2+
= 2+ 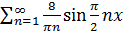
Задание № 4
Вариант 1.
1. Найти полный дифференциал функции двух переменных:  .
.
2. Исследовать на экстремум функцию:  .
.
Вариант 2.
1. Найти полный дифференциал функции двух переменных:  .
.
2. Исследовать на экстремум функцию:  .
.
Вариант 3.
1. Найти полный дифференциал функции двух переменных:  .
.
2. Исследовать на экстремум функцию:  .
.
Вариант 4.
1. Найти полный дифференциал функции двух переменных:  .
.
2. Исследовать на экстремум функцию: 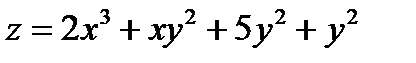 .
.
Вариант 5.
1. Найти полный дифференциал функции двух переменных: 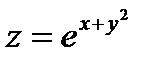 .
.
2. Исследовать на экстремум функцию:  .
.
Вариант 6.
1. Найти полный дифференциал функции двух переменных:  .
.
2. Исследовать на экстремум функцию:  .
.
Вариант 7.
1. Найти полный дифференциал функции двух переменных: 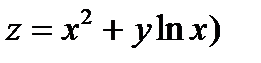 .
.
2. Исследовать на экстремум функцию: 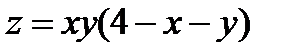 .
.
Вариант 8.
1. Найти полный дифференциал функции двух переменных: 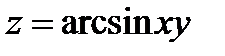
2. Исследовать на экстремум функцию: 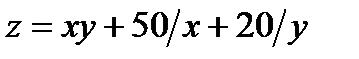 ,
, 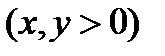 .
.
Вариант 9.
1. Найти полный дифференциал функции двух переменных:  .
.
2. Исследовать на экстремум функцию: 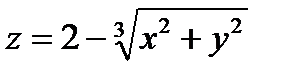 .
.
Вариант 10.
1. Найти полный дифференциал функции двух переменных: 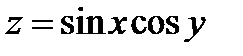
2. Исследовать на экстремум функцию: