а)  – расчетный срок, временной интервал
– расчетный срок, временной интервал  , текущий год
, текущий год 
б) по топливным базам
 – удельные капвложения на расширение добычи топлива,
– удельные капвложения на расширение добычи топлива,
 – удельные затраты на добычу топлива.
– удельные затраты на добычу топлива.
в) ТЭС
 – удельные капвложения на
– удельные капвложения на  -ой станции при работе на
-ой станции при работе на  -м топливе,
-м топливе,
 – число часов использования установленной мощности,
– число часов использования установленной мощности,
 – удельный расход топлива.
– удельный расход топлива.
Обычно  и
и  зависят от
зависят от  и
и  и при увеличении мощности эти коэффициенты обычно уменьшаются. Чтобы работать с линейной моделью, эти нелинейности не учитываются и используются в виде констант.
и при увеличении мощности эти коэффициенты обычно уменьшаются. Чтобы работать с линейной моделью, эти нелинейности не учитываются и используются в виде констант.
Составление математической модели начинается с выбора переменных. Обозначим неизвестные установленные мощности в период t на возможных площадках  при использовании возможных видов топлива с баз
при использовании возможных видов топлива с баз  как
как  .Обозначим потоки по возможным линиям от КЭС к нагрузкам как
.Обозначим потоки по возможным линиям от КЭС к нагрузкам как  .
.
Для линий, которые связывают нагрузочные узлы, вводят две переменные, каждая из которых определяет поток мощности в одном из возможных направлений  ,
,  . Это связано с требованием неотрицательности переменных в задачах линейного программирования. В оптимальном решении обе или одна из этих переменных обязательно окажется свободной, т.е. будет равна нулю.
. Это связано с требованием неотрицательности переменных в задачах линейного программирования. В оптимальном решении обе или одна из этих переменных обязательно окажется свободной, т.е. будет равна нулю.
Составим целевую функцию, которая должна учитывать затраты на сооружение станций, ЛЭП и затраты на топливо:
 , (2.15)
, (2.15)
где  – суммарные затраты для одного временного сечения.
– суммарные затраты для одного временного сечения.
Общие затраты:
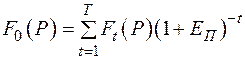 , (2.16)
, (2.16)
где 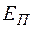 – коэффициент дисконтирования.
– коэффициент дисконтирования.
Определим ориентировочно составляющие затрат.
· Затраты в КЭС:
 , (2.17)
, (2.17)
где первое слагаемое – капитальные вложения на вводимые мощности в период t; второе слагаемое – затраты на амортизацию; третье слагаемое – ежегодные издержки, где  – себестоимость выработки без топливной составляющей.
– себестоимость выработки без топливной составляющей.
· Затраты в ЛЭП в год  :
:

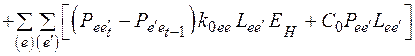 , (2.18)
, (2.18)
где  – стоимость одного километра линии;
– стоимость одного километра линии;
 – коэффициент аппроксимации нижней огибающей затрат.
– коэффициент аппроксимации нижней огибающей затрат.
· Затраты на топливо в год  :
:
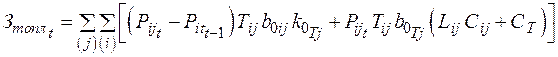 , (2.19)
, (2.19)
где  – капвложения в добычу;
– капвложения в добычу; 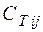 – удельная стоимость транспорта топлива;
– удельная стоимость транспорта топлива; 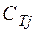 – удельная стоимость добычи топлива;
– удельная стоимость добычи топлива;  – удельный расход топлива.
– удельный расход топлива.
Составим систему уравнений и неравенств, учитывающих свойства системы и её связи.
1. Условие покрытия дефицита мощности:
 . (2.20)
. (2.20)
2. Условие баланса мощности на шинах каждой станции:
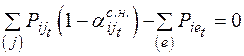 . (2.21)
. (2.21)
3. Условие баланса в узлах нагрузок:
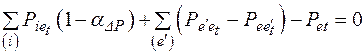 . (2.22)
. (2.22)
4. Ограничения по установленной мощности станции:
 . (2.23)
. (2.23)
5. Ограничения по допустимому объему ввода мощности на отрезке  :
:
 . (2.24)
. (2.24)
6. Ограничения по объему топлива:
 . (2.25)
. (2.25)
7. Если  , то необходимо учитывать условие покрытия дефицита энерги.
, то необходимо учитывать условие покрытия дефицита энерги.
 . (2.26)
. (2.26)
В модели могут учитываться и другие ограничения, например, пропускная способность ЛЭП  .
.
В динамической модели все рассмотренные ограничения прописываются для каждого временного разреза t, что резко увеличивает размерность модели.
Если динамическая модель не вписывается в возможности ЭВМ, то динамику учитывают оптимизацией статических моделей отдельно для каждого момента времени  .
.
Для дальнейшего сокращения оптимизационных моделей можно использовать метод декомпозиции, т.е. разделение на подсистемы (рис. 2.5). В каждой подсистеме имеются возможные площадки и нагрузки, что позволяет формировать и решать оптимизационные модели отдельно для каждой подсистемы с учетом фиксированных значений возможных перетоков обменной мощности с соседними подсистемами. В результате оптимизации для каждой подсистемы находятся установленные мощности электростанций и потоки по внутренним линиям.


Рис. 2.5 Рис. 2.6
Кроме моделей подсистем составляется координационная модель, в которой каждая подсистема рассматривается в виде узла (см. рис. 2.6). Показатели генерирующих станций (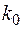 ,
,  ,
,  ) в каждом узле определяются показателями самой неэкономичной электростанции из числа использованных в каждой подсистеме, называемых «замыкающими».
) в каждом узле определяются показателями самой неэкономичной электростанции из числа использованных в каждой подсистеме, называемых «замыкающими».
Оптимизация координационной линейной модели позволяет найти целесообразные потоки мощности между подсистемами с учетом экономических показателей их замыкающих электростанций, ограничивая использование самых неэкономичных.
После этого вновь проводится оптимизация моделей всех подсистем при найденных перетоках, определяются замыкающие станции и вновь оптимизируется координационная модель. Итерационный процесс проводится до тех пор, пока с заданной точностью не стабилизируются потоки между подсистемами.
В качестве примера рассмотрим упрощенную статическую линейную оптимизационную модель.
Пример 2.2. Составим модель для системы, имеющей дефицит 800 МВт, 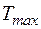 = 5000 ч,
= 5000 ч, 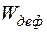 = 4000·103 МВт·ч.
= 4000·103 МВт·ч.
Для покрытия дефицита возможно сооружение КЭС-1 и КЭС-2. На КЭС-1 могут вводиться блоки по 100 и 200 МВт на каменном угле с максимальной установленной мощностью 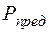 = 600 МВт. На КЭС-2 планируются блоки 100 МВт на буром угле при
= 600 МВт. На КЭС-2 планируются блоки 100 МВт на буром угле при 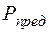 = 400 МВт. Выделяемые годовые объемы топлива не должны превышать по каменному углю 1800·103 т у.т.; по бурому углю 600·103 т у.т.
= 400 МВт. Выделяемые годовые объемы топлива не должны превышать по каменному углю 1800·103 т у.т.; по бурому углю 600·103 т у.т.
Технико-экономические показатели:
| ТЭП | 200У | 100У | 100Б |
 , , 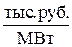
| |||
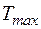 , ч , ч
| |||
 , , 
| 0,335 | 0,4 | 0,67 |
Для наглядности изобразим планируемую систему в виде упрощенной схемы (рис. 2.7) и введем переменные х1, х2 и х3, которыми обозначим неизвестные установленные мощности в группах из однотипных блоков.
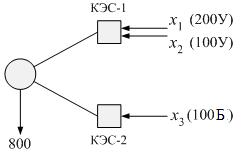
Рис. 2.7
Составим ограничения:
1. По условию покрытия дефицита мощности:
 .
.
2. Условие покрытия дефицита энергии:
 .
.
3. Ограничение по топливу (уголь):
 .
.
4. Ограничение по топливу (бурый уголь):
 .
.
5. Ограничение по установленным мощностям:
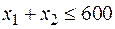 ,
,  .
.
Целевая функция:
 .
.
Решение модели на ЭВМ дает следующий результат:
 ,
, 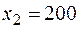 ,
,  ,
,  ,
,  ,
, 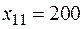 ,
, 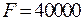 .
.
Появившиеся в решении  ,
, 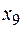 ,
,  являются фиктивными, вводимыми программой для перехода от неравенств к равенствам при решении по симплекс-методу.
являются фиктивными, вводимыми программой для перехода от неравенств к равенствам при решении по симплекс-методу.
Таким образом, оптимальная структура генерирующих мощностей наКЭС-1: 2×200 + 2×100 и на КЭС-2: 2×100; 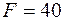 млн. руб.
млн. руб.
На рисунке 2.8 приведена реализация решения по программе SimpleX.

Рис. 2.8
Для решения задач линейного программирования могут использоваться и другие программы. Ниже на рисунке 2.9 приведена реализация решения в пакете MathCAD 2001 Professional. Здесь дополнительно введено ограничение на получение неотрицательных решений, т.е.  . Для удобства отображения результата полученный вектор решений транспонируем, чтобы решения были записаны не в столбец, а в строчку (
. Для удобства отображения результата полученный вектор решений транспонируем, чтобы решения были записаны не в столбец, а в строчку ( ).
).


Рис. 2.9
2.5. Применение динамического программирования
для выбора площадок
Как известно, метод динамического программирования ориентирован на оптимизацию многошаговых процессов. Процесс условной оптимизации может развиваться от начала к конечному состоянию и наоборот.
В динамическом программировании рассматриваются:
· состояние  системы;
системы;
· управление  на шаге;
на шаге;
· эффективность  на шаге;
на шаге;
· условная оптимальная эффективность  , определяющая общий эффект на всех оптимизированных шагах до
, определяющая общий эффект на всех оптимизированных шагах до  -го включительно для каждого состояния
-го включительно для каждого состояния  .
.
Основное уравнение динамического программирования при оптимизации от конечного состояния  к начальному состоянию
к начальному состоянию  :
:
 , (2.27)
, (2.27)
и от начального  к конечному
к конечному  :
:
 . (2.28)
. (2.28)
Рассмотрим упрощенный пример выбора плана ввода мощностей для покрытия возрастающего дефицита 400, 500, 600 МВт для трех временных разрезов  . Для покрытия могут использоваться три площадки с возможными для ввода блоками 100 МВт.
. Для покрытия могут использоваться три площадки с возможными для ввода блоками 100 МВт.
Все особенности сооружения учтены в стоимости каждой электростанции в зависимости от возможной мощности её и представлены в таблице 2.1.
Таблица 2.1
| ЭС | ||||
Диаграмма процесса условной оптимизации приведена на рисунке 2.10.

Рис. 2.10
В качестве этапов принят процесс ввода мощностей только на одной станции. В качестве состояния  примем установленную мощность всех электростанций, которые введены на рассмотренных этапах
примем установленную мощность всех электростанций, которые введены на рассмотренных этапах  ; управление
; управление  – ввод мощности на каждой станции
– ввод мощности на каждой станции  ; эффективность на шаге
; эффективность на шаге  – стоимость вводимой мощности
– стоимость вводимой мощности  ; условная оптимальная эффективность
; условная оптимальная эффективность  – общая стоимость на всех рассмотренных этапах.
– общая стоимость на всех рассмотренных этапах.
Оптимальная траектория процесса ввода мощностей определяется обратным ходом, двигаясь из конечного состояния к началу в соответствии с найденными и запомненными условно-оптимальными управлениями. Результаты оптимизации представлены в таблице 2.2.
Таблица 2.2
| ЭС-1 | ЭС-2 | ЭС-3 | ЗО (затраты общие) | |
| t = 1 | 2×100 | |||
| t = 2 | 2×100 | 2×100 | ||
| t = 3 | 3×100 | 2×100 |
2.6. Оптимизация в условиях
вероятностно-определенной информации
Как было отмечено ранее, в больших системах наряду с детерминированной информацией рассматривается также вероятностно-определенная и неопределенная. Пусть оптимизируемый параметр  , подверженный случайному изменению, лежит в диапазоне
, подверженный случайному изменению, лежит в диапазоне  и для него известен закон распределения. На рисунке 2.11 приведены примеры двух законов распределения.
и для него известен закон распределения. На рисунке 2.11 приведены примеры двух законов распределения.
Равномерное распределение

| Нормальное распределение

|
| а) | б) |
Рис. 2.11
В природе чаще проявляется нормальное распределение. Для определения вероятности попадания х в любой интервал при этом используется функция Лапласа. Она позволяет определять эту вероятность при любом значении  . но для этого случайную величину x заменяют нормированной
. но для этого случайную величину x заменяют нормированной
 .
.
В диапазоне  и определены таблицы Лапласа.
и определены таблицы Лапласа.
Таблица 2.3
Значения функции Лапласа
| t | Ф (t) | t | Ф (t) | T | Ф (t) | t | Ф (t) |
| 0,0 | 0,0000 | 1,0 | 0,3413 | 2,0 | 0,4772 | 3,0 | 0,4986 |
| 0,1 | 0,0398 | 1,1 | 0,3643 | 2,1 | 0,4821 | 3,1 | 0,4990 |
| 0,2 | 0,0793 | 1,2 | 0,3849 | 2,2 | 0,4861 | 3,2 | 0,4993 |
| 0,3 | 0,1179 | 1,3 | 0,4032 | 2,3 | 0,4893 | 3,3 | 0,4995 |
| 0,4 | 0,1554 | 1,4 | 0,4192 | 2,4 | 0,4918 | 3,4 | 0,4997 |
| 0,5 | 0,1915 | 1,5 | 0,4332 | 2,5 | 0,4938 | 3,5 | 0,4998 |
| 0,6 | 0,2257 | 1,6 | 0,4452 | 2,6 | 0,4953 | 3,6 | 0,49984 |
| 0,7 | 0,2580 | 1,7 | 0,4554 | 2,7 | 0,4965 | 3,7 | 0,49989 |
| 0,8 | 0,2881 | 1,8 | 0,4641 | 2,8 | 0,4974 | 3,8 | 0,49993 |
| 0,9 | 0,3159 | 1,9 | 0,4713 | 2,9 | 0,4981 | 3,9 | 0,49995 |
Эти таблицы определяют вероятность попадания  в интервал от
в интервал от  до
до  , который пропорционален площади кривой (рис. 2.12):
, который пропорционален площади кривой (рис. 2.12):
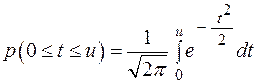 . (2.29)
. (2.29)
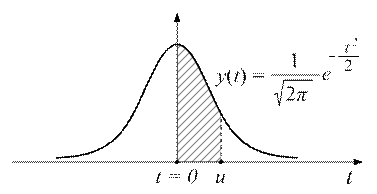
Рис. 2.12
В соответствии с этим интересующая вероятность попадания  в интервал от
в интервал от  до
до 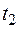 (рис. 2.13) определяется по выражению:
(рис. 2.13) определяется по выражению:
 ,
,
 ,
,  .
.

Рис. 2.13
Если в качестве случайного параметра рассматривается прогнозируемое математическое ожидание мощности нагрузочного узла с определенным значением стандартного отклонения при нормальном законе распределения, то весь диапазон изменения нагрузки в пределах  можно разбить на дискретные ступени любой ширины, например, равной
можно разбить на дискретные ступени любой ширины, например, равной  (рис. 2.14). Для каждой ступени по таблице Лапласа можно определить вероятность рi попадания случайной мощности в рассматриваемый интервал, принимая для интервала среднее значение мощности.
(рис. 2.14). Для каждой ступени по таблице Лапласа можно определить вероятность рi попадания случайной мощности в рассматриваемый интервал, принимая для интервала среднее значение мощности.
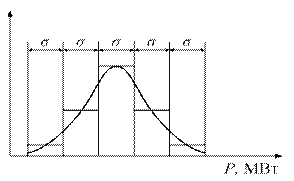
Рис. 2.14
В этом случае для оценки какого-либо возможного варианта развития системы необходимо рассмотреть все интервалы и для каждого i -го интервала по средней мощности внутри него определить затраты Зi. Общие затраты для варианта оцениваются математическим ожиданием затрат равным
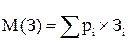 .
.
При выборе наилучшего варианта развития системы или её объекта для каждого проводятся аналогичные расчеты. Объем вычислений возрастает при учете двух и более параметров режима с поинтервальной оценкой их значений. Поэтому учет вероятностно-определенной информации оправдан при использовании метода сравнения вариантов, в которых лишь несколько параметров задаются вероятностными показателями.
В оптимизационных моделях сложных систем переменные с вероятностно определенной информацией учитываются их математическими ожиданиями.

2.7. Определение типа электростанции в условиях
неопределенности
Выбираемый тип электростанций во многом зависит от неопределенности условий, которые могут возникнуть в будущем. Примерами таких условий могут быть условия обеспечения топливом, риски и последствия аварий, требования экологии, экономическая коньюнктура, политическая ситуация и др.
При выборе типа в условиях неопределенности можно использовать основные критерии теории игр.
Оценим тип электростанции для покрытия дефицита электроэнергии в регионе, где рассматривается возможность сооружения АЭС на быстрых или тепловых нейтронах наряду с другими путями покрытия дефицита энергии. Основные сложности применения методов теории игр связаны с выбором стратегий природы, которая выступает в роли нашего противника и непреднамеренно «генерирует» неопределенности, а также наших стратегий и, наконец, составления платежной матрицы.
В рассматриваемой задаче примем 4 следующих неопределенности.
1. Обеспеченность ресурсами природного газа с освоенных месторождений.
2. Риск аварий на АЭС с тяжелыми последствиями.
3. Проблема с поставками газа.
4. Наличие большого количества радиоактивных отходов и риски их распространения.
Возможные пути энергоснабжения (типы электростанций):
1. Реактор на быстрых нейтронах БН-800.
2. Водо-водяной энергетический реактор ВВЭР-1000.
3. Покупка энергии на оптовом рынке.
4. Тепловая станция на угле (КЭС).
Таким образом, в формализуемой игре у каждого игрока по 4 стратегии. Составим платежную матрицу, определив экспертным путем ожидаемые ущербы для каждой пары стратегий. Эта часть игровых методов наиболее ответственная и трудоемкая. Конечно, для обоснования величины ущербов требуется всесторонний и глубокий анализ, поэтому не стоит искать обоснования приведенным ущербам. Платежная матрица, матрица рисков R и оптимальные стратегии показаны на рисунке 2.15.
При решении рассматривались следующие критерии теории игр:
1) min max,
2) min min,
3) критерий Гурвица (γ = 0,5),
4) критерий Лапласа,
5) min max по матрице риска R.

Рис. 2.15
Ущербы при оптимальных стратегиях подчеркнуты. Как видно чаще всех в состав оптимальных стратегий по разным критериям попадает вариант АЭС на энергетических реакторах типа ВВЭР.
2.8. Выбор оптимальных планов развития электрической сети
2.8.1. Общие положения
Планирование развития сети проводится после того, как с помощью линейной модели выбраны типы блоков и сроки их ввода, а также определены варианты развития основной сети, хотя и достаточно приближенно. Задача выбора оптимального плана развития электрических сетей гораздо сложнее из-за большой размерности, наличия дискретных переменных (сечений проводов ЛЭП и номинальных мощностей трансформаторов) и учета графа сети. При решении её используется метод декомпозиции, в соответствии с которым сеть разбивается на подсети по территориальному признаку, либо по назначению (системообразующие сети, местные сети, распределительные сети).
При планировании развития распределительной сети могут использоваться методы решения транспортной задачи, которая заключается в поиске таких связей между заданными нагрузками  и существующими или новыми подстанциями с известной мощностью
и существующими или новыми подстанциями с известной мощностью  из числа возможных с известной длиной
из числа возможных с известной длиной  , по которым обеспечиваются все нагрузки при минимальных затратах. Если в качестве переменных принять потоки от
, по которым обеспечиваются все нагрузки при минимальных затратах. Если в качестве переменных принять потоки от  -ой подстанции к
-ой подстанции к  -ой нагрузке
-ой нагрузке  , то математическая модель описывается ограничениями двух типов: предельной мощностью центров питания и балансами по каждой нагрузке
, то математическая модель описывается ограничениями двух типов: предельной мощностью центров питания и балансами по каждой нагрузке
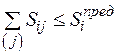 , (2.30)
, (2.30)
 . (2.31)
. (2.31)
Целевая функция определяется как сумма произведений длины на поток по каждой возможной линии
 . (2.32)
. (2.32)
Решение задачи позволяет оптимальным образом распределить нагрузки между питающими центрами.
При выборе плана развития сети совместно решаются три задачи:
1) выбор номинального напряжения электрической сети  ;
;
2) выбор конфигурации (динамического графа);
3) выбор сечения проводов и кабелей.
Рассмотрим некоторые особенности решения этих задач.