Как известно, шкала номинальных напряжений электрических сетей свыше 1000 В общего назначения переменного тока определяется по ГОСТ 721-77 и рекомендует для вновь проектируемых сетей следующие напряжения:
6, 10, 35, 110, 220, 330, 500, 750, 1150 кВ.
При выборе напряжения необходимо учитывать сложившиеся системы напряжений в Европейской части России 110(150)/330/750 кВ и на Урале и в Сибири – 110/220/500/1150 кВ.
Предварительно выбор напряжения может быть произведен по эмпирической формуле Г.А. Илларионова:
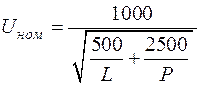 , (2.33)
, (2.33)
где 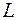 – длина линии, км;
– длина линии, км; 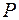 – передаваемая по цепи мощность, МВт.
– передаваемая по цепи мощность, МВт.
Данная формула дает удовлетворительные результаты для всей шкалы номинальных напряжений переменного тока в диапазоне 35–1150 кВ.
Существуют и другие эмпирические формулы для выбора номинального напряжения. Область их применения ограничивается некоторыми условиями, представленными ниже (табл. 2.4).
Таблица 2.4
Формулы для выбора номинального напряжения передачи
| Формула Стилла | Формула А.М. Залесского |
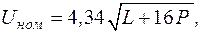
| 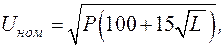
|
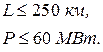
| 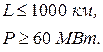
|
Области применения стандартных номинальных напряжений в зависимости от мощности и дальности электропередачи приведены на рисунке 2.16 и в таблице 2.5.
Таблица 2.5
Пропускная способность электропередачи 110–1150 кВ
| Uном, кВ | F, мм2 | Натуральная мощность, МВт, при волновом сопротивлении, Ом | Наибольшая передаваемая мощность на одну цепь, МВт | Наибольшая длина передачи, км | ||
| 400 | 300–314 | 250–275 | ||||
| 70-240 | – | – | 25-50 | 50-150 | ||
| 240-400 | – | 100-200 | 150-250 | |||
| 2×240-2×400 | – | 300-400 | 200-300 | |||
| 3×330-3×500 | – | 700-900 | 800-1200 | |||
| 5×240-5×400 | – | – | 1800-2200 | 1200-2000 | ||
| 8×300-8×500 | – | – | 4000-6000 | 2500-3000 |
Сегодня две сложившиеся в России системы имеют шаг по номинальному напряжению внутри каждой примерно равный 2 и разницу по передаваемой мощности для смежных напряжений в 4÷6 раз. Это приводит к тому, что при передаче определённой мощности, на низком напряжении потребуется несколько цепей, а при высоком напряжении линия будет недогружена. В связи с этим при выборе напряжения можно использовать соседние по ПУЭ Uном, но с увеличенным радиусом расщепления.
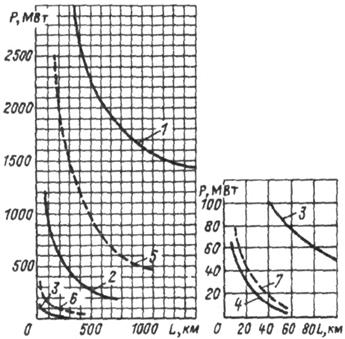
Рис. 2.16. Области применения электрических сетей разных номинальных напряжений. Указаны границы равноэкономичности: 1 –1150 и 500 кВ; 2 – 500 и 220 кВ; 3 – 220 и 110 кВ; 4 – 110 и 35 кВ; 5 – 750 и 330 кВ; 6 – 330 и 150 кВ; 7 – 150 и 35 кВ
Конфигурация
При выборе схем развития электрических сетей могут использоваться следующие приемы:
а) реконструкция магистральной передачи путем добавления второй цепи, иногда на более высоком напряжении;
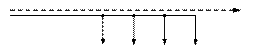
Рис. 2.17
б) появление новых кольцевых линий;
в) глубокий ввод на более высоком напряжении.

Рис. 2.18
Безусловно, окончательный выбор напряжения и конфигурации должен проводиться на основе технико-экономических расчетов.
Выбор сечения
При выборе сечения необходимо учитывать явление короны, по которому определяется минимальное допустимое сечение для каждого номинального напряжения.
Максимально допустимое сечение для ЛЭП зависит от номинального напряжения и определяется рациональным соотношением расходов цветного и черного металла в конструкцию линии.
Выбор сечения осуществляется по экономической плотности тока или экономическим интервалам. Экономическая плотность определяется по минимуму затрат в ЛЭП и зависит от типа линии, материала провода, графика нагрузки.
2.8.2. Экономические интервалы
Использование экономических интервалов позволяет исключить из числа переменных дискретные сечения и номинальные мощности трансформаторов. С помощью экономических интервалов удается представить затраты в виде функции только от передаваемой мощности. При выборе структуры генерирующих мощностей затраты в ЛЭП можно представить в виде 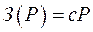 . При планировании развития сети можно использовать более точную аппроксимацию в виде
. При планировании развития сети можно использовать более точную аппроксимацию в виде 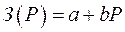 или
или 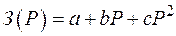 , но все они имеют разрыв при
, но все они имеют разрыв при 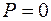 . В качестве непрерывной функции может использоваться аппроксимация вида
. В качестве непрерывной функции может использоваться аппроксимация вида 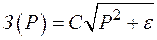 , по которой при
, по которой при 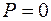 затраты
затраты 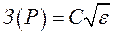 могут быть уменьшены подбором ε.
могут быть уменьшены подбором ε.
При выборе экономических интервалов для трансформаторов затраты учитываются следующей формулой:
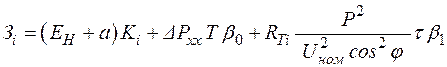 , (2.34)
, (2.34)
где 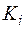 – стоимость
– стоимость  -ого трансформатора;
-ого трансформатора;  – время работы трансформатора;
– время работы трансформатора;
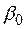 – стоимость потерянной энергии, определяемая затратами на базисных ЭС;
– стоимость потерянной энергии, определяемая затратами на базисных ЭС;
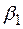 – стоимость, определяемая затратами в пиковых станциях.
– стоимость, определяемая затратами в пиковых станциях.
Обычно 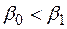 , но часто принимают
, но часто принимают 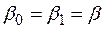 .
.
Из условия 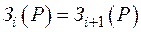 определяется верхняя граница
определяется верхняя граница 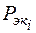 экономического интервала трансформатора с номинальной мощностью
экономического интервала трансформатора с номинальной мощностью 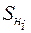 .
.
2.8.3. Математическая модель планирования развития сети
Формирование модели начинают с составления расчетной схемы, где показываются существующие узлы и ветви, новые узлы и возможные дополнительные трассы линий, связывающих объекты в систему. Здесь должны учитываться и те линии, которые были найдены в результате анализа модели по выбору структуры генерирующих мощностей. Расчетная схема должна быть разумно избыточной и включать дополнительные линии, так чтобы не пропустить возможные оптимальные связи.
Для узлов должны быть заданы прогнозируемые нагрузки и мощности вводимых блоков. Таким образом, расчетная схема будет иметь 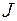 расчетных узлов, из них
расчетных узлов, из них 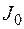 – существующих; т.е. индекс узлов
– существующих; т.е. индекс узлов 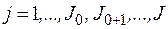 . Число ветвей в расчетной схеме
. Число ветвей в расчетной схеме  , из которых
, из которых 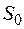 – существующих.
– существующих.
В качестве неизвестных можно принять потоки активной мощности по ветвям 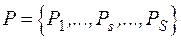 .
.
В качестве целевой функции рассмотрим затраты в существующие линии, пропорциональные потерям энергии, и в новые линии, определяемые в соответствии с принятыми аппроксимирующими выражениями для затрат:
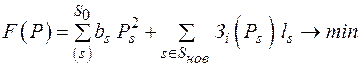 , (2.35)
, (2.35)
где 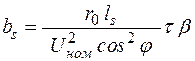 .
.
На неизвестные потоки мощности по ветвям накладывается условие баланса мощностей в узлах, которое может быть записано в матричной форме:
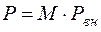 .
.
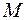 – прямоугольная матрица соединений узлы-ветви, причем ее элементы для узла и ветви s обозначаются
– прямоугольная матрица соединений узлы-ветви, причем ее элементы для узла и ветви s обозначаются 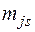 и могут принимать значения, равные 1, если ветвь выходит из узла; +1, если ветвь входит в узел и 0, если она не связана с узлом.
и могут принимать значения, равные 1, если ветвь выходит из узла; +1, если ветвь входит в узел и 0, если она не связана с узлом.
Составим уравнение баланса для узла (рис. 2.19):
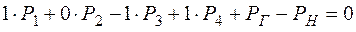 .
.
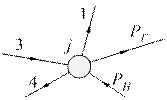
Рис. 2.19
В общем виде уравнение баланса для любого  -ого узла можно записать:
-ого узла можно записать:
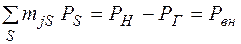 .
.
Таким образом, задача выбора оптимальной схемы сети заключается в поиске минимума некоторой нелинейной функции 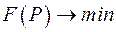 при соблюдении линейного ограничения в форме равенства
при соблюдении линейного ограничения в форме равенства 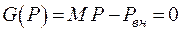 .
.
Сформулированная таким образом задача планирования развития сети сводится к задаче нелинейного программирования. Эта задача, как правило, имеет один экстремум. Для решения её могут использоваться рассмотренные ранее методы нелинейного программирования.
2.8.4. Применение градиентных методов
Как известно, основное уравнение градиентного метода:
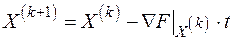 . (2.36)
. (2.36)
Рассмотрим пример, в котором необходимо выбрать сеть для питания только одного узла (рис. 2.20). Полагаем, что затраты представлены квадратичными зависимостями. В качестве исходной точки примем Р 0=(0, РН).
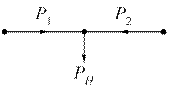
| 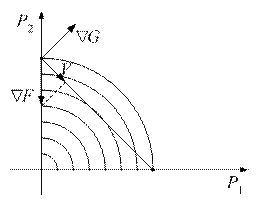
| В любой точке должно выполняться ограничение G(P)= P 1+ P 2- P н=0 |
Рис. 2.20
При учете ограничений движение к минимуму должно осуществляться по проекции градиента на поверхность ограничений, т.е. вдоль вектора V. Вектор V можно получить путем исключения из 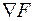 составляющих, перпендикулярных поверхности ограничений. Эти составляющие образуют градиент ограничений
составляющих, перпендикулярных поверхности ограничений. Эти составляющие образуют градиент ограничений 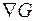 . Таким образом, вектор V определяется по выражению
. Таким образом, вектор V определяется по выражению
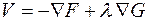 . (2.37)
. (2.37)
Для определения неопределенных множителей 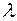 , образующих вектор V, используется условие равенства нулю скалярного произведения:
, образующих вектор V, используется условие равенства нулю скалярного произведения:
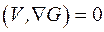 . (2.38)
. (2.38)
Из этого условия, приняв для линейного ограничения градиент равным 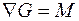 , можно найти
, можно найти 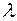 . Действительно, из преобразования
. Действительно, из преобразования
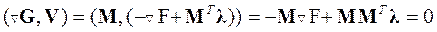 (2.39)
(2.39)
можно получить следующее матричное выражение для множителей 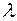
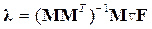 . (2.40)
. (2.40)
Составляющие вектора множителей λ позволяют определить все составляющие вектора V
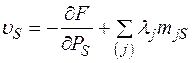 ,
,
и использовать их в процедуре градиентного метода
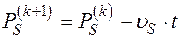 .
.
Однако, найти проекцию градиента можно проще, если в (2.37) подставить выражение (2.40) и провести несложное преобразование
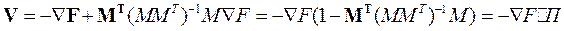 , (2.41)
, (2.41)
где П = 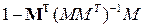 - матрица проектирования.
- матрица проектирования.
Итерационный процесс продолжается до тех пор, пока не выполнится условие требуемой точности для всех составляющих 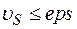 .
.
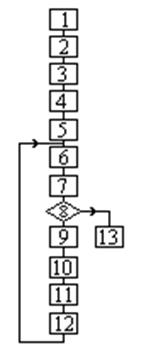 Рис. 2.21
Рис. 2.21
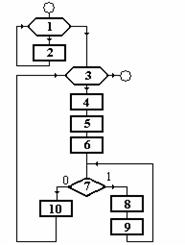
| Блок-схема алгоритма с выбором оптимального шага приведена на рисунке 2.21. Назначение блоков:
1. Формирование расчетной схемы.
2. Определение типа функций для расчета затрат и их
производных для всех ветвей.
3. Формирование матрицы инциденций М.
4. Определение матрицы проектирования градиента П.
5. Исходное приближение потоков Р=Р0.
6. Вычисление градиента 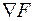 в точке Р.
7. Определение проекции V градиента.
8. Проверка условия окончания в точке Р.
7. Определение проекции V градиента.
8. Проверка условия окончания 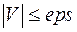 .
9. Организация пробного шага Р1= Р- V t0/.
10. Вычисление градиента и проекции V 1 в конце шага.
11. Определение оптимального шага .
9. Организация пробного шага Р1= Р- V t0/.
10. Вычисление градиента и проекции V 1 в конце шага.
11. Определение оптимального шага
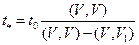 .
12. Рабочий шаг .
12. Рабочий шаг 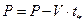 .
13. Вывод результатов .
13. Вывод результатов
|
Пример 2.3. Определить оптимальные потоки в ветвях сети, расчетная схема которой приведена на рисунке 2.22.
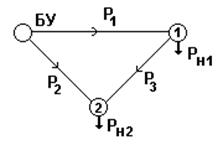 Рис. 2.22
Рис. 2.22
| Определен вид предикторов, формирующих целевую функцию
F(P)=5P12+10P22+10P32,
для которой определены составляющие вектор-градиента. Для схемы составлена матрица Ми расчетом определена матрица проектирования.
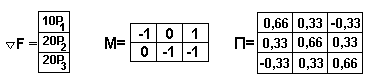
|
Итерационный расчет начинается с принятия исходного приближения Р0, определения величины градиента и проекции его на поверхность ограничений
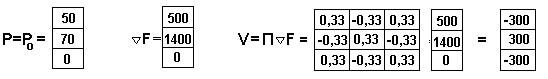
Затем в направлении проекции делается пробный шаг t0=0,1 и определяются потоки по ветвям Р1 в конце этого шага, градиент и его проекция

После этого можно определить шаг, близкий к оптимальному
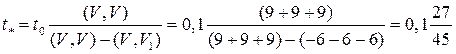 =0,06
=0,06
и выполнить рабочий шаг из исходной точки Р по направлению проекции 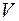
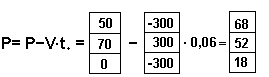
После этого в соответствии с алгоритмом возвращаемся к блоку 6, где вновь вычисляется градиент и его проекция
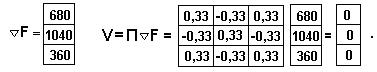
Проверка условия в блоке 8 определяет завершение итерационного процесса.
По найденным потокам можно выбирать сечение ЛЭП.
Быстрая сходимость процесса объясняется квадратичным характером целевой функции, которая имеет линейный градиент и оптимальный шаг, найденный по двум точкам приводит к точному решению.
Недостатком метола является большая размерность задачи, определяемая количеством ветвей расчетной схемы.
2.8.5. Метод покоординатной оптимизации
В расчетной схеме, как правило, минимальным является число контуров, определяемое как разность числа ветвей и узлов. Поэтому при оптимизации в качестве неизвестных целесообразно использовать контурные мощности и применить метод покоординатного поиска. Преимущество этого метода в том, что на каждом шаге оптимизации целевой функции 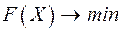 выбирается только одна переменная
выбирается только одна переменная 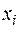 при фиксированных значениях остальных. Найденное значение
при фиксированных значениях остальных. Найденное значение 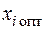 фиксируется, и затем переходят к оптимизации следующей переменной
фиксируется, и затем переходят к оптимизации следующей переменной 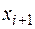 и т.д.
и т.д.
Рассмотрим балансовое ограничение 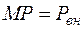 . Все потоки по ветвям можно разделить на две составляющие:
. Все потоки по ветвям можно разделить на две составляющие:
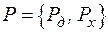 ,
,
где 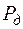 – потоки в дереве, ветви которого связывают все узлы с балансирующим без образования контуров;
– потоки в дереве, ветви которого связывают все узлы с балансирующим без образования контуров;
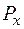 –потоки в хордах, т.е. в ветвях, образующих контуры.
–потоки в хордах, т.е. в ветвях, образующих контуры.
Основное ограничение 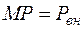 можно представить разделенным на блочные матрицы, как показано на рисунке 2.23.
можно представить разделенным на блочные матрицы, как показано на рисунке 2.23.
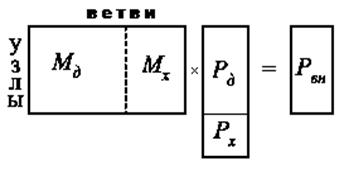
Рис. 2.23
Потоки в ветвях дерева однозначно определяются потоками в хордах, что следует из соотношений, полученных на основе операций с блочными матрицами, и представленных ниже:
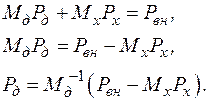 (2.42)
(2.42)
В качестве исходного приближения можно принять:
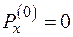 .
.
Тогда потоки в деревьях:
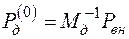 .
.
В качестве хорд могут быть выбраны разные ветви исходной схемы, дополняющие выделенное дерево с образованием контуров. Число комбинаций определяется возможным количеством деревьев, рассчитываемых с помощью определителя Трента,формируемого для независимых узлов:
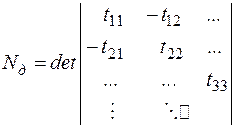 , (2.43)
, (2.43)
где 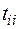 – число ветвей, связанных с узлом
– число ветвей, связанных с узлом 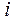 ;
; 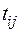 – число ветвей, связывающих узлы
– число ветвей, связывающих узлы  и
и  .
.
Пример 2.4. Определить число деревьев для схемы
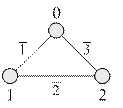
| 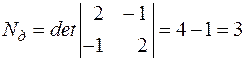
|
Рис. 2.24
Контурная оптимизация осуществляется по следующему алгоритму.
1) Составляется расчетная схема.
2) Определяются зависимости для учета затрат в линии расчетной схемы. Для этого могут использоваться любые аппроксимирующие функции вплоть до точной нижней огибающей затрат в новые линии.
3) Выбираются и нумеруются хорды, для которых принимается исходное приближение потоков 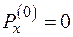 , и считаются потоки в ветвях дерева.
, и считаются потоки в ветвях дерева.
4) Организуется цикл по хордам, в котором последовательно выполняются следующие операции:
– для текущей хорды просматривается контур, который она замыкает;
– по принятому потоку в хорде определяются потоки в ветвях контура;
– по потокам в ветвях контура считаются затраты в каждую ветвь и общие затраты во все ветви контура;
– последовательно изменяя значение потоков хорды в сторону возрастания или убывания, при этом определяются новые потоки в ветвях контура и новые затраты, которые сравниваются с предыдущими до поиска минимума.
Таким образом, проводится оптимизация. Если затраты считаются по аппроксимации 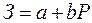 , то можно рассматривать такие потоки в хорде, при которых в контуре появляется ветвь с нулевой мощностью, что обеспечивает минимум затрат. После этого текущая хорда переносится в эту ветвь.
, то можно рассматривать такие потоки в хорде, при которых в контуре появляется ветвь с нулевой мощностью, что обеспечивает минимум затрат. После этого текущая хорда переносится в эту ветвь.
5) После выхода из цикла новое положение хорд сравнивается с предыдущим. Если оно не совпадает, то осуществляется очередной цикл оптимизации. При совпадении расчет заканчивается. Обычно достаточно двух-трех циклов.
Пример 2.5. Выбрать оптимальный план развития сети 220 кВ, которая представлена на рисунке 2.25-а.
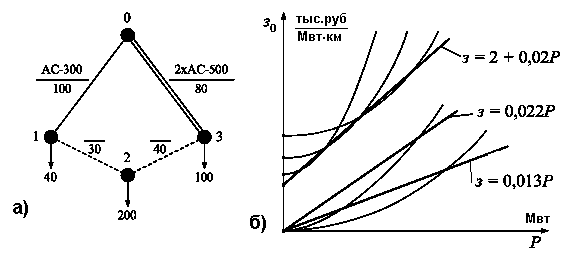
Рис. 2.25
Для рассматриваемой сети развитие связано с ростом нагрузок и подключением новой подстанции. Пунктиром показаны возможные трассы ЛЭП. На рисунке 2.25-б приведены кривые затрат в существующие и новые ЛЭП и их линейные аппроксимации.
В таблице приведены выражения для определения затрат в каждую ветвь расчетной схемы с учетом длины.
Таблица 2.6
| Линия | Затраты |
| 0-1 | 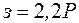
|
| 1-2 | 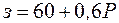
|
| 2-3 | 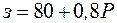
|
| 0-3 | 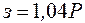
|
В расчетной схеме всего 1 контур и в качестве начального положения хорды примем участок 2-3. Выделим все ветви контура для расчета затрат. Итерационный процесс представлен в таблице 2.7:
Таблица 2.7
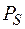
| 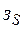
| 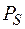
| 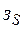
| 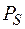
| 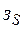
| |
| 0-1 | ||||||
| 1-2 | ||||||
| 2-3 | ||||||
| 0-3 | ||||||
В исходном положении хорды затраты составили 812 тыс.руб. Перемещение хорды в соседнее положение привело к изменению потоков и снизило затраты. Дальнейшее перемещение в том же направлении оказалось уже не выгодным.
В результате оптимизации находится дерево, соответствующее минимальным затратам.
Для сети любой сложности итеративный процесс сходится достаточно быстро. При этом могут использоваться специальные быстрые алгоритмы, применяемые для разомкнутых сетей. Они основаны на методе «вторых адресных отображений».
Найденное в результате оптимизации дерево определяет основу развивающейся сети, которая может дополняться с учетом требований надежности и качества режима.
Рассмотрим суть метода вторых адресных отображений, который может использоваться при выборе оптимального дерева развивающейся сети. Рассмотрим разомкнутую схему (рис. 2.26), по которой от центра питания нагрузка поступает к нескольким потребителям. При заданных узловых нагрузках, например токовых, ток каждой ветви определяется простым суммированием токов тех узлов, которые проходят через эту ветвь. Если схема сети задана парами узлов для каждой ветви строго в направлении от ЦП, что является вполне естественным, то порядковый номер начального узла ветви в списке (массиве) конечных узлов позволит легко организовать проход от любого узла до ЦП, который для завершения пути должен иметь особый номер, например отрицательный. Найденные таким образом для каждой ветви номера и называют «вторыми адресами».
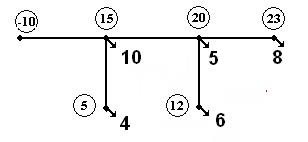
Рис. 2.26
Таблица 2.8
| № пп | УН | УК | ТУ | УН2 | Ток ветви (ТВ) |
| -10 | -10 | 10+4+6+8+5=33 | |||
| 5+4+8=17 | |||||
В таблице показаны исходные данные и этапы расчета токов ветвей. Обозначения массивов здесь: УН – узлы начала, УК – узлы конца ветвей, ТУ– токи узлов, ТВ – токи ветвей, УН2 – вторые адресные отображения.
Анализируя таблицу, следует обратить внимание на то, что при правильно заданной конфигурации сети каждый номер узла в массиве УН можно найти в массиве УК. Как уже отмечалось, место его, т.е. порядковый номер, в этом массиве и называют вторым адресным отображением.
Найденные адреса могут использоваться для определения токов в ветвях, потоков мощности, потерь, т.е. для расчета режима. Рассмотрим порядок определения токов по ветвям. Здесь сначала все элементы массива ТУ переписываются в массив ТВ, а затем токи всех узлов, начиная с последнего, накладываются путем суммирования на токи ветвей, по которым узел запитан от пункта питания в соответствии с вторыми адресами.
Аналогично проводится расчет потокораспределения мощностей, учет потерь мощности и напряжения.
Рассмотрим два алгоритма, используемых при анализе разомкнутых сетей.
На рисунке 2.27 приведена блок-схема алгоритма определения вторых адресов, а на рисунке 2.28 блок-схема алгоритма расчета токораспределения.
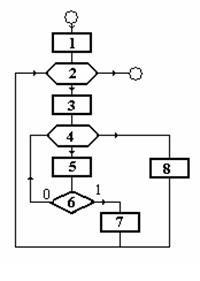
| Назначение блоков алгоритма: 1. УН2(1)= –10 2. Цикл по узлам i=2…n 3. к1=УН(i) 4. Внутренний цикл по узлам j=1…n 5. к2=УК(j) 6. Проверка условия к1=к2? 7. УН2(i)= j 8. Вывод сообщения «Потеря связности. Узел с номером к1 не запитан.» |
Рис. 2.27
В алгоритме контурной оптимизации развивающейся сети хорды объединяются в отдельный массив, где формируются и вторые адреса для обоих узлов разомкнутой ветви. В цикле оптимизации для каждой хорды определяется питающий узел, выполняющий роль ЦП и ограничивающий перемещение положения хорды в процессе одномерной оптимизации.
| Функции блоков алгоритма: 1. Цикл по узлам i=1…n 2. ТВ(i)= ТУ(i) 3. Цикл по узлам i=1…n 4. j= n– i+1 5. ум= ТУ(j) 6. м=УН2(j) 7. Проверка условия м<0? 8. ТВ(м)= ТВ(м)+ум 9. м=УН2(м) 10. ТВ(1)= ТВ(1)+ум |
Рис. 2.28
2.8.6. Метод «ветвей и границ» (МВГ) для выбора оптимальной
распределительной сети
Распределительные сети, как правило, эксплуатируются по разомкнутым схемам. Основой для выбора новой сети является поиск дерева минимальных затрат. Число возможных деревьев огромно и определятся определителем Трента. Оптимальное дерево можно найти путем расчета затрат для каждого дерева из всего множества возможных деревьев. Но такой просмотр всех комбинаций не реален даже при современных ЭВМ.
Суть метода ветвей и границ заключается в разбиении всего множества возможных планов на подмножества с последующей упрощенной оценкой эффективности каждого и отбрасыванием (исключением из дальнейшего анализа) неперспективных подмножеств. По сути это комбинаторный метод, но с целенаправленным перебором вариантов. Метод впервые появился в 1960 году для решения задачи линейного целочисленного программирования, но оказался незамеченным, и лишь в 1963 году был эффективно использован для решения задачи о коммивояжере, который должен объехать все коммерческие пункты по кратчайшему пути. Подобную задачу решают и спортсмены ориентировщики.
Исходное множество 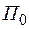 и все текущие разбиваются на непересекающиеся подмножества
и все текущие разбиваются на непересекающиеся подмножества 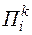 , где
, где  – номер разбиения,
– номер разбиения, 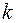 – порядковый номер подмножества на этапе разбиения (рис. 2.29).
– порядковый номер подмножества на этапе разбиения (рис. 2.29).
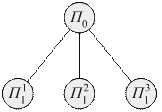
Рис. 2.29
Для исходного множества существует неизвестный план с минимальными затратами
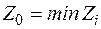 , (2.44)
, (2.44)
где 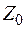 – точная нижняя граница затрат, которая неизвестна;
– точная нижняя граница затрат, которая неизвестна;
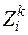 – точная нижняя граница затрат, которая также существует для
– точная нижняя граница затрат, которая также существует для 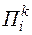 .
.
Полагаем, что имеется возможность для достаточно простого определения некоторой внешней оценки затрат 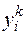 для этого подмножества, для которой выполняется условие
для этого подмножества, для которой выполняется условие 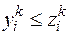 . Эту оценку можно использовать для выявления «дорогих» подмножеств, которые можно исключить из дальнейшего разбиения. Для повышения надежности в конкурентных подмножествах рассматривают еще и внутренние оценки
. Эту оценку можно использовать для выявления «дорогих» подмножеств, которые можно исключить из дальнейшего разбиения. Для повышения надежности в конкурентных подмножествах рассматривают еще и внутренние оценки 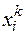 , для которых
, для которых 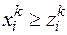 . Внешние и внутренние оценки показаны на рисунке 2.30.
. Внешние и внутренние оценки показаны на рисунке 2.30.

Рис. 2.30
Перспективные подмножества делятся аналогично. Процесс ветвления продолжается до тех пор, пока в подмножестве не останется несколько вариантов (2÷4) или не совпадут внешние и внутренние оценки 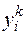 =
= 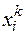 .
.
Рассмотрим применение идеи метода ветвей и границ для задачи поиска новой распределительной сети с линейной аппроксимацией затрат в ветви расчетной схемы
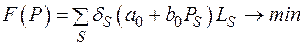 , (2.45)
, (2.45)
где 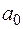 ,
,  – коэффициенты аппроксимации в выражении удельных затрат
– коэффициенты аппроксимации в выражении удельных затрат
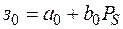 ;
; 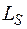 – длина возможных трасс для линий;
– длина возможных трасс для линий; 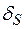 – дельта-функция;
– дельта-функция; 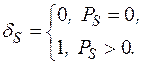
Минимум определяется с учетом линейных ограничений по балансу:
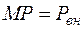 .
.
При реализации идеи метода ветвей и границ для решения любой комбинаторной задачи надо определить правила разбиения на подмножества, найти наиболее простой способ вычисления внешней и внутренней оценки точной нижней границы затрат для любого подмножества.
В поставленной задаче разбиение осуществляется на два подмножества, которые отличаются только наличием или отсутствием какой-либо конкретной ветви, например, ветви 1 (рис. 2.31).
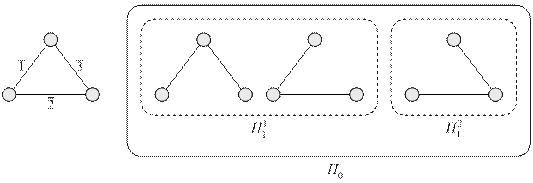
|
Рис. 2.31
Подмножества, полученные в результате такого разбиения, являются непересекающимися
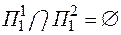 ,
,
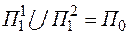 .
.
Найдем способ определениявнешней оценки точной нижней границы. Для этого рассмотрим точную нижнюю границу
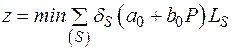 , (2.46)
, (2.46)
и заменим ее, разбив на две суммы
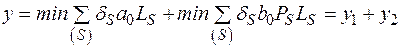 . (2.47)
. (2.47)
Каждая из составляющих может определяться по известным методам:
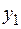 пропорциональна сумме длин и определяет дерево минимальной длины;
пропорциональна сумме длин и определяет дерево минимальной длины;
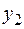 – определяет дерево с минимальными затратами на транспорт, пропорциональными произведениям потоков мощности на дину.
– определяет дерево с минимальными затратами на транспорт, пропорциональными произведениям потоков мощности на дину.
Для обеих составляющих существуют и известны методы определения.
Первая составляющая 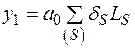 – затраты в кратчайшее дерево, определяемые по алгоритму Прима, суть которого в последовательном вычеркивании самой длинной ветви графа, не допуская потери связности.
– затраты в кратчайшее дерево, определяемые по алгоритму Прима, суть которого в последовательном вычеркивании самой длинной ветви графа, не допуская потери связности.
Вторая составляющая 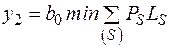 определяется решением транспортной задачи.
определяется решением транспортной задачи.
Если 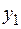 и
и 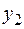 соответствуют одному и тому же дереву, то, очевидно, что
соответствуют одному и тому же дереву, то, очевидно, что
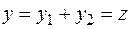 .
.
Если 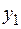 и
и 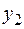 соответствуют разным деревьям, то
соответствуют разным деревьям, то 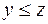 .
.
Таким образом, найдена достаточно хорошая внешняя оценка, позволяющая из двух подмножеств оставлять для дальнейшего ветвления то, которое имеет меньшую внешнюю границу.
В качестве внутренней оценки могут выступать затраты 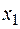 , соответствующие полным затратам в дерево кратчайшей длины; либо
, соответствующие полным затратам в дерево кратчайшей длины; либо 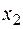 , определяемые по полным затратам в дерево, найденное по транспортному алгоритму. Еще лучше определять эту оценку по условию
, определяемые по полным затратам в дерево, найденное по транспортному алгоритму. Еще лучше определять эту оценку по условию
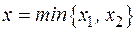 .
.
Внутренняя оценка используется для подтверждения целесообразности выбора перспективного подмножества, если для него при сравнении с внешней оценкой отбрасываемого подмножества выполняется условие 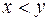 .
.
Пример 2.4. Выбрать оптимальное дерево для новой сети, возможные ветви которой показаны на рисунке 2.32.
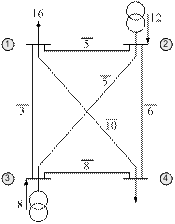 Рис. 2.32
Рис. 2.32
|
Распределительная сеть предназначена для питания нагрузок Р1= 16и Р4= 4. Все мощности и затраты представлены в относительных единицах.
Длины возможных ветвей показаны на схеме. Затраты на 1 км для всех линий определяются предиктором 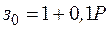 .
Задача заключается в выборе дерева минимальных затрат. .
Задача заключается в выборе дерева минимальных затрат.
|
Определим общее число деревьев в исходном множестве
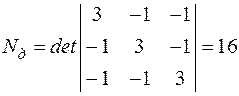 .
.
На рисунке 2.33 показан состав исходного множества 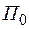 деревьев, разделенных на 2 непересекающихся подмножества.
деревьев, разделенных на 2 непересекающихся подмножества.
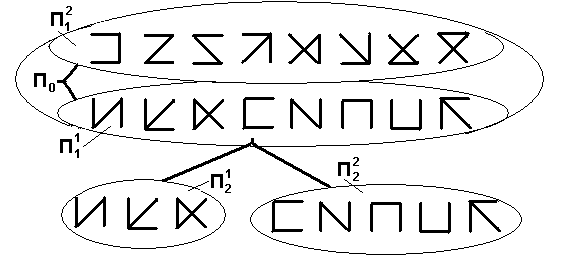
Рис. 2.33
Найдем для исходного множества 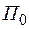 внешнюю оценку
внешнюю оценку 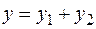 .
.
| Определим кратчайшее дерево по алгоритму Прима | 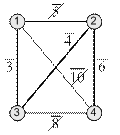
| 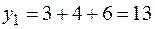
|
| Составим и решим транспортную задачу | 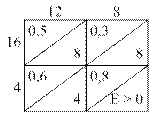
| 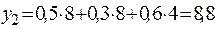
|
В результате получим 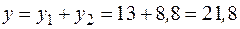 .
.
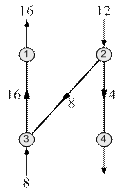
Найдем внутреннюю оценку, определив ее полными затратами в кратчайшее дерево:
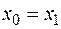
| 
| 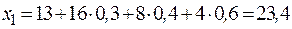
|
Разделим исходное множество на два подмножества, приняв за контрольную самую короткую ветвь. Найдем внешнюю границу для подмножества 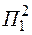 , которое не имеет этой ветви.
, которое не имеет этой ветви.
| По алгоритму Прима | 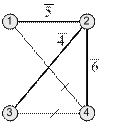
| 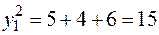
|
| Транспортная задача | 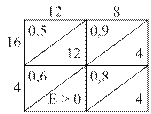
| 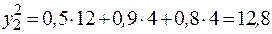
|
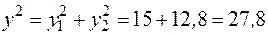 .
.
Оценки для П11 совпадают с оценками для По. По результатам сравнения внешних границ подмножество  исключается из дальнейшего ветвления.
исключается из дальнейшего ветвления.
Подмножество П11 делится аналогично на два по ветви 3-2(рис. 2.32). Схема ветвления показана на рисунке 2.34.
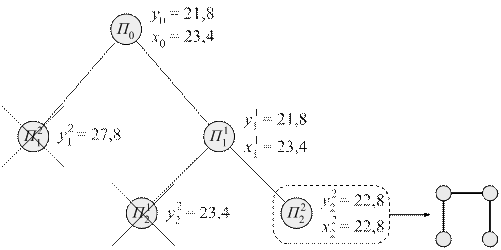
Рис. 2.34
В результате анализа подмножества 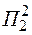 внешняя и внутренняя оценки совпали. Найденное дерево и является оптимальным для планируемой распределительной сети.
внешняя и внутренняя оценки совпали. Найденное дерево и является оптимальным для планируемой распределительной сети.
Таким образом, в рассматриваемой сети проведен анализ примерно 1/4 части всех деревьев. В сложных схемах, где число деревьев значительно больше, эффективность метода гораздо выше.
2.9. Учет надежности и экологии
Математические модели, какими бы сложными они не были, не могут учесть все особенности и критерии рассматриваемой системы. Как правило, в первую очередь учитывается критерий экономичности. Надежность в первом приближении учитывается числом цепей. Экология может учитываться заданием предельных мощностей электростанций или ограничениями по предельно допустимым концентрациям (ПДК) выбросов различных веществ (COX, NOX и др.), т.е. учитываться по удельным выходам 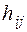 каждого
каждого  -ого продукта выброса в г/(кВт·ч) или в г/кВт:
-ого продукта выброса в г/(кВт·ч) или в г/кВт:
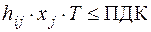 ;
;
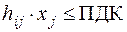 ,
,
где 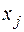 – установленная мощность.
– установленная мощность.
Треб