Если  ,
,  , то
, то
1.  . 2.
. 2. 
3. 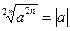 . 4.
. 4.  .
.
5.  . 6.
. 6.  .
.
7.  . 8.
. 8.  .
.
9.  . 10.
. 10.  .
.
Логарифмы и их свойства
 .
.
Основное логарифмическое тождество:  .
.
1.  .
.
2.  .
.
3.  .
.
4.  .
.
5.  .
.
6.  .
.
7.  .
.
8.  .
.
Основные тригонометрические тождества
 ;
;  ;
;
 ;
;  ;
;
 ;
;  .
.
Формулы сложения
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
 .
.
Формулы двойного аргумента
 ;
;  ;
;
 ;
;  ;
;
 .
.
Формулы половинного аргумента
 ;
;  ;
;
 .
.
Формулы преобразования суммы в произведение
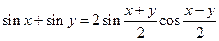 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
Формулы преобразования произведения в сумму
 ;
;
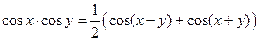 ;
;
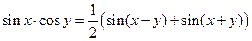 .
.
Обратные тригонометрические функции
 ;
;
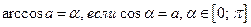 ;
;
 ;
;
 .
.
 ;
;
 ;
;
 ;
;
 .
.
Таблица некоторых значений тригонометрических функций
| Аргумент Функция | 
| 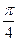
| 
| 
| 
| 
| 
| 
| |
| 00 | 300 | 450 | 600 | 900 | 1200 | 1350 | 1500 | 1800 | |
| sin x | 
| 
| 
| 
| 
| 
| |||
| cos x | 
| 
| 
| - 
| - 
| - 
| -1 | ||
| tg x | 
| 
| - | - 
| -1 | - 
| |||
| ctg x | - | 
| 
| - 
| -1 | - 
| - |
| Аргумент Функция | 
| 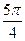
| 
| 
| 
| 
| 
| 2 
|
| 2100 | 2250 | 2400 | 2700 | 3000 | 3150 | 3300 | 3600 | |
| sin x | - 
| - 
| - 
| -1 | - 
| - 
| - 
| |
| cos x | - 
| - 
| - 
| 
| 
| 
| ||
| tg x | 
| 
| - | - 
| -1 | - 
| ||
| ctg x | 
| 
| - 
| -1 | - 
| - |
Простейшие тригонометрические уравнения
| Уравнение | Решение |
 , где , где 
| 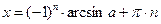 , где , где 
|
 , где , где 
|  , где , где 
|

|  , где , где 
|

|  , где , где 
|
Частные случаи
| Уравнение | Решение |

|  , где , где 
|

|
 , где , где 
|

|  , где , где 
|

|
 , где , где 
|

|  , где , где 
|
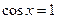
|
 , где , где 
|
Основные элементарные функции и их графики
Степенная функция у = хα, где где α – действительное число. Например,


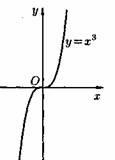



Показательная функция  , где a >0, a ≠ 1.
, где a >0, a ≠ 1.

Логарифмическая функция  , где a >0, a ≠ 1.
, где a >0, a ≠ 1.

Тригонометрические функции 

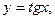
 .
.



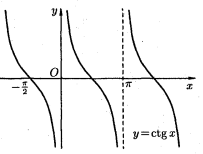
Обратные тригонометрические функции
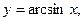

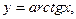
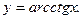

Производные основных элементарных функций
1.  . 2.
. 2.  .
.
3.  . 4.
. 4.  .
.
5.  . 6.
. 6.  .
.
7.  . 8.
. 8.  .
.
9.  . 10.
. 10. 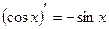 .
.
11.  . 12.
. 12.  .
.
13.  . 14.
. 14.  .
.
15.  . 16.
. 16.  .
.
Основные правила дифференцирования
1.  . 2.
. 2.  .
.
3.  . 4.
. 4.  ,
,
где С – постоянная величина и функции  и
и 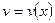 имеют производные.
имеют производные.
Свойства неопределенных интегралов
1.  .
.
2.  .
.
3.  , где
, где  .
.
4.  ,
,
где  , С – произвольная постоянная.
, С – произвольная постоянная.
Таблица основных интегралов
1.  .
.
2.  .
.
3.  , где п ≠-1.
, где п ≠-1.
4.  .
.
5.  , где а >0, а ≠1.
, где а >0, а ≠1.
6. 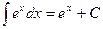 .
.
7.  .
.
8.  .
.
9.  .
.
10.  .
.
11.  .
.
12.  .
.
13.  .
.
14.  , где а ≠0.
, где а ≠0.
15.  , где -1< x <1.
, где -1< x <1.
16.  .
.
17.  .
.
18. 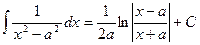 , где а ≠0.
, где а ≠0.
19.  , где а ≠0.
, где а ≠0.
Формула Ньютона-Лейбница для вычисления определенного интеграла:
 ,
,
где  .
.
Свойства определенного интеграла
1.  .
.
2.  , где
, где  .
.
3. 
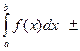
 .
.
4. 
 .
.
5. 
 +
+ 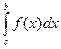 , где
, где  .
.
6. Если  на отрезке
на отрезке  и
и  , то
, то 
 .
.
Площадь плоской фигуры

где у = f2 (x), y = f 1(x) – уравнения верхней и нижней границ фигуры; х = а, х = b – уравнения левой и правой границ фигуры.
Формулы комбинаторики



Классическое определение вероятности:
 ,
,
где m – число благоприятных исходов опыта; n – число всех равновозможных исходов
Относительная частота события:
Р *(А) =  ,
,
где m – число наступлений события А; n – число всех проведенных испытаний
Теорема сложения вероятностей несовместных событий:
Р (А1+А2+…+Аn) =Р (А1) +Р (А2) +…+Р (Аn).
Теорема умножения вероятностей двух зависимых событий:
Р (А  .
.
Теорема умножения вероятностей независимых событий:
 .
.
Теорема сложения вероятностей двух совместных событий:

Вероятность противоположного события:

Вероятность появления хотя бы одного из событий:
P (A 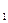 +A
+A  +A…+A
+A…+A  ) = 1– P (
) = 1– P (
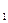 ) P (
) P (
 )
)  ).
).
Треугольник
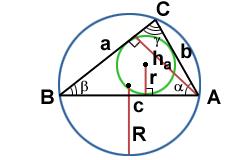
a, b, с – длины сторон треугольника;
h – высота треугольника;
γ – угол между сторонами a и b;
r – радиус вписанной окружности;
R – радиус описанной окружности;
 – периметр треугольника;
– периметр треугольника;
 – полупериметр треугольника;
– полупериметр треугольника;
 – площадь треугольника;
– площадь треугольника;
 – формула Герона;
– формула Герона;
 – площадь треугольника по двум сторонам и углу между ними;
– площадь треугольника по двум сторонам и углу между ними;
 – площадь треугольника по тремсторонам и радиусу описанной окружности;
– площадь треугольника по тремсторонам и радиусу описанной окружности;
 – площадь треугольника по трем сторонам и радиусу вписанной окружности.
– площадь треугольника по трем сторонам и радиусу вписанной окружности.
Прямоугольный треугольник

a, b – катеты; c – гипотенуза;
 – теорема Пифагора;
– теорема Пифагора;
 – площадь прямоугольного треугольника;
– площадь прямоугольного треугольника;
 ;
;  ;
;  – соотношения в прямоугольном треугольнике;
– соотношения в прямоугольном треугольнике;
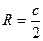 – радиус описанной около прямоугольного треугольника окружности.
– радиус описанной около прямоугольного треугольника окружности.