§3 Критерии проверки и оценка решений заданий 15 (18 в 2015 г., С3 ранее) вариантов КИМ ЕГЭ–2016
Напомним, что на этом месте в КИМ 2011–2014 гг была система двух неравенств, а в 2015 и 2016 году заявлено решение одного неравенства. Грубо говоря, задание №15 «в два раза» проще прежнего задания С3.
Среди различных причин такого изменения отметим внутреннюю для задач на решение неравенств. Дело в том, что критерии проверки задания С3 были весьма лаконичны, жестко структурированы, но в то же время и достаточно беспощадны. Вполне грамотный и хорошо подготовленный выпускник, который допускал в решении каждого из неравенств системы хотя бы по одной неточности, получал 0 из возможных 3 баллов, несмотря на все достижения, которые он продемонстрировал в процессе решения. Например, это приводило к тому, что оценка «2 балла» из трёх была более редкой, чем оценка «3 балла» из трёх.
При переходе к решению одного неравенства поле возможностей при выставлении 0, 1 или 2 баллов несколько расширяется. При этом сразу же подчеркнём, что в данном случае оценка «1 балл» не есть половина оценки «2 балла». Другими словами, утверждение «1 балл ставится, если задача решена наполовину» неверно. Более точным является тезис, выражаемый равенством «1 = 2-» или словами «1 балл ставится, если задача почти решена». Для получения 1 балла за выполнение задания №15 необходимо получение итогового ответа и наличие верной последовательности всех шагов решения. Вот как в точности выглядят критерии оценивания выполнения задания №15.
| Содержание критерия, №17 (ЕГЭ – 2015) | Баллы |
| Обоснованно получен верный ответ | |
| Обоснованно получен ответ, отличающийся от верного исключением точки …, ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения | |
| Решение не соответствует ни одному из критериев, перечисленных выше | |
| Максимальный балл |
Вот одно из видоизменений, связанных с конкретикой задания.
| Содержание критерия №17 (ЕГЭ – 2015) | Баллы |
| Обоснованно получен верный ответ | |
| Обоснованно получен ответ, отличающийся от верного включением граничных точек, ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения | |
| Решение не соответствует ни одному из критериев, перечисленных выше | |
| Максимальный балл |
При этом в первом случае выставления 1 балла допускаются только ошибки в строгости неравенства: « » вместо «
» вместо «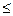 », или наоборот. Если в ответ включено значение переменной, при котором одна из частей неравенства не имеет смысла, то следует выставлять оценку «0 баллов».
», или наоборот. Если в ответ включено значение переменной, при котором одна из частей неравенства не имеет смысла, то следует выставлять оценку «0 баллов».
Мы использовали решения заданий №15 из материалов ЕГЭ предыдущего года, а также задания диагностических работ. В них задачи №15 несколько моделируют те типы неравенств, которые встречались в заданиях С3. Были выбраны примеры решения в основном по показательным неравенствам.
Следующие ниже примеры решений мы намеренно приводим в весьма лаконичном стиле. Кратко говоря, это «минимальное» решение, за которое можно выставить максимальный балл.
Задача 1.
Решите неравенство  .
.
Ответ: 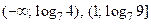 .
.
Решение. Относительно  неравенство имеет вид:
неравенство имеет вид:
 ,
,
откуда  или
или  . Возвращаясь к
. Возвращаясь к 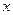 , получаем:
, получаем:  или
или 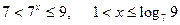 .
.
Ответ:  .
.
Вот как выглядят в данном случае критерии выставления 1 балла.
«Обоснованно получен ответ, отличающийся от верного ответа исключением точки  ; ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения».
; ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения».
При включении в ответ  или х = 1 ставится оценка «0 баллов».
или х = 1 ставится оценка «0 баллов».
Задача 2.
Решите неравенство  .
.
Решение. Относительно 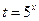 неравенство имеет вид:
неравенство имеет вид:
 ,
,
откуда  или
или  .
.
Возвращаясь к 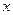 , получаем
, получаем  .
.
Ответ: 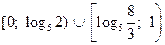 .
.
Вот как выглядят в данном случае критерии выставления 1 балла.
«Обоснованно получен ответ, отличающийся от верного ответа исключением точек х = 0 и/или х =  ; ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения».
; ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения».
При включении в ответ х = 1 или х =  ставится оценка «0 баллов».
ставится оценка «0 баллов».
Задача 3.
Решите неравенство  .
.
Решение. Относительно  неравенство имеет вид:
неравенство имеет вид:
 ,
,
откуда  или
или  . Возвращаясь к
. Возвращаясь к 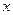 , получаем
, получаем  или
или 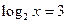 ,
,  .
.
Ответ:  .
.
Вот как выглядят в данном случае критерии выставления 1 балла.
«Обоснованно получен ответ, отличающийся от верного ответа исключением точки х = 8; ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения».
При включении в ответ х = 0 или х =  ставится оценка «0 баллов».
ставится оценка «0 баллов».