Пример 1. В остроугольном треугольнике 
провели высоту 
. Из точки 
на стороны 
и 
опустили перпендикуляры 
и 
соответственно.
а) Докажите, что треугольник 
подобен треугольнику .
б) Найдите отношение площади треугольника к площади четырёхугольника 
, если 
, а радиус окружности, описанной около треугольника , равен 4. Ответ: 
.
Комментарий.
Доказательство в пункте а верно, хотя в первой строке – описка. В б есть ошибка по невнимательности (12 вместо 8) при нахождении коэффициента подобия, но присутствуют «верно» выполненные все шаги решения.
Оценка эксперта: 2 балла.
Пример 2. См. задача 1. Ответ: б) 30.
Комментарий. Доказательство в пункте а верно. В б (4-я строка, б) есть ошибка: утверждение 
неверно.
Оценка эксперта: 1 балл.
Пример 3.
Точка 
лежит на отрезке 
. Прямая, проходящая через точку 
, касается окружности с диаметром в точке 
и второй раз пересекает окружность
с диаметром в точке 
. Продолжение отрезка 
пересекает окружность с диаметром в точке 
.
а) Докажите, что прямые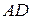 
и 
параллельны.
б) Найдите площадь треугольника 
, если 
и 
.
Ответ: б) 30.
Комментарий.
Доказательство в пункте а верно. Решение задачи пункта б отсутствует.
Оценка эксперта: 1 балл.
Пример 4.
Точка B лежит на отрезке AC. Прямая, проходящая через точку A, касается окружности с диаметром BC в точке M и второй раз пересекает окружность с диаметром AB в точке K. Продолжение отрезка MB пересекает окружность с диаметром AB в точке D.
а) Докажите, что прямые AD и MC параллельны.
б) Найдите площадь треугольника DBC, если AK = 3 и MK = 14. Ответ: б) 
.
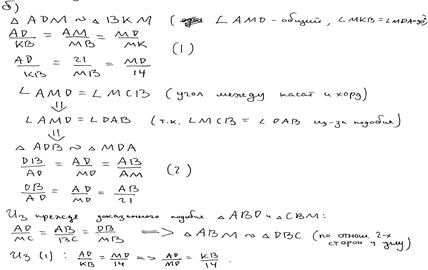
Комментарий. Доказательство в пункте, а верно. Пункт б содержит много верных утверждений, но в этом пункте получен неверный ответ не из-за арифметической ошибки. Верно найдена площадь треугольника АВМ. Но далее автор решения не заметил, что треугольники АВМ и CBD – равновелики!
|
|
Оценка эксперта: 1 балл.
Пример 5.
Точка лежит на отрезке . Прямая, проходящая через точку , касается окружности с диаметром в точке и второй раз пересекает окружность
с диаметром в точке . Продолжение отрезка пересекает окружность с диаметром в точке .
а) Докажите, что прямые 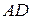и параллельны.
б) Найдите площадь треугольника , если 
и .
Ответ: 
Комментарий.
Доказательство в пункте, а верно. Пункт б не содержит неверных утверждений и результатов вычислений. В частности, автор решения увидел, что фигура AMCD – трапеция и значит, треугольники АВМ и CBD – равновелики!
Оценка эксперта: 3 балла.
§5 Критерии проверки и оценка решений заданий 17 (19 в 2015 г.) вариантов КИМ ЕГЭ–2016
Введение текстовых задач экономического содержания в ЕГЭ–2015 по математике стало, пожалуй, наиболее заметным изменением во всем комплексе заданий КИМ с развёрнутым ответом. Во всех заданиях этого типа предыдущих лет условие с самого начала формулировалось в математических терминах и отдельно не предполагало построения какой-либо математической модели (частично этот момент мог присутствовать в некоторых способах решения заданий С5 с параметром). Некоторое исключение составляло задание С6, в котором явно текстовое, сюжетное, условие задачи на начальном этапе решения предполагало некоторый перевод на математический язык. Правда, сами тексты условий чаще всего уже активно использовали математическую терминологию: числа, записанные на доске, делимость, доли и дроби, средние величины и т.п.
|
|
В заданиях №17 (=19) существенно усилена сюжетная, практико–ориентированная, составляющая условия. Относительно существования (возможностей существования) непосредственных связей этих задач с окружающей нас действительностью можно составить отдельный трактат. Мы ограничимся лишь констатацией двух положений. Во-первых, сами сюжеты не есть прямые цитаты «из жизни», они априорно уже являются некоторыми текстовыми упрощениями, моделями, реально возникающих ситуаций. Во-вторых, эти сюжеты условно можно разделить на два типа, использующих соответственно дискретные модели (проценты, погашения кредитов, …) и непрерывные модели (различные производства, протяженные во времени, объемы продукции, …). Процитируем критерии оценивания выполнения заданий №19 из КИМ-2015.
| Содержание критерия, задание 17 (=19) | Баллы |
| Обоснованно получен верный ответ | |
| Верно построена математическая модель, решение сведено к исследованию этой модели и получен результат: — неверный ответ из-за вычислительной ошибки; — верный ответ, но решение недостаточно обосновано | |
| Верно построена математическая модель, решение сведено к исследованию этой модели, при этом решение может быть не завершено | |
| Решение не соответствует ни одному из критериев, перечисленных выше | |
| Максимальный балл |
Несколько подробнее, 1 балл можно выставлять в тех случаях, когда сюжетное условие задачи верно сведено к решению математической (арифметической алгебраической, функциональной, геометрической) задачи. Именно к решению, а не к отдельному равенству, набору уравнений, уравнению, задающему функцию и т.п. Грубо говоря, предъявленный текст должен включать направление, «продолжаемое» до верного решения. Оценка в 2 балла, разумеется, включает в себя условия выставления 1 балла, но существенно ближе к верному решению задачи.
|
|
Здесь предполагается завершенное, практически полное решение соответствующей математической задачи. Типичные допустимые погрешности здесь – вычислительные ошибки (при наличии всех шагов решения) или недостаточно полные обоснования. Например, при отыскании экстремума решение ограничивается верным нахождением лишь критической точки, без надлежащей её проверки на экстремальность. Кратко, «2 = 3- ».
Отметим, что термин «математическая модель», быть может, излишне высокопарен для сравнительно простых задач экономического содержания, предлагаемых на ЕГЭ. Однако, по нашему мнению, он наиболее лаконичен, общеупотребим и достаточно ясен для того, чтобы пытаться отыскать ему адекватную замену. Следует подчеркнуть, что один и тот же сюжет может быть успешно сведен к различным математическим моделям (см. ниже задачу 2) и доведён до верного решения. По этой причине в критериях проверки нигде нет жесткого упоминания о какой-либо конкретной (алгебраической, геометрической, функциональной, …) модели.
Вообще, способов верного решения заданий этого типа никак не меньше, чем для привычных текстовых задач. Возможен и стиль, приближенный к высшей математике, и наивный подход, напоминающий арифметический способ решения текстовых задач, и метод использующий специфические для математической экономики понятия (целевая функция, симплекс-метод и т.п.).
Задача 1.
1 июня 2013 года Всеволод Ярославович взял в банке 900 000 рублей в кредит. Схема выплаты кредита следующая – 1 числа каждого следующего месяца банк начисляет 1 процент на оставшуюся сумму долга (то есть увеличивает долг на 1%), затем Всеволод Ярославович переводит в банк платёж. На какое минимальное количество месяцев Всеволод Ярославович может взять кредит, чтобы ежемесячные выплаты были не более 300 000 рублей?