Решение №1.1 («по-взрослому»).

Минимизировать время выплат можно, только максимизировав сами выплаты. Решим задачу в общем виде. Пусть сумма (в тыс. руб.) кредита; задолженность в й месяц; – выплата в й месяц, 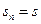; коэффициент ежемесячного повышения, . Тогда

После предпоследней выплаты останется и тогда в последний, й раз, кредит будет погашен. Значит, .

Относительно 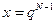получаем неравенство

.

По условию , т.е. ,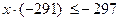

Так как , то .

Ответ: 4.

Решение №1.2 («по-детски»).

Если бы банк не брал процентов, то долг можно было бы вернуть за 3 месяца. Банк за 3 месяца возьмет меньше, чем 3% от первоначальной суммы в 900 тыс., т.е. меньше 27 тыс. Поэтому то, что забирает банк, точно можно будет оплатить в 4-й месяц, потратив меньше 300 тыс.

Ответ: 4.

Задача 2.

15-го января был выдан полугодовой кредит на развитие бизнеса. В таблице представлен график его погашения.

В конце каждого месяца, начиная с января, текущий долг увеличивался на 5%, а выплаты по погашению кредита происходили в первой половине каждого месяца, начиная с февраля. На сколько процентов общая сумма выплат при таких условиях больше суммы самого кредита?

Решение. Пусть 15-го числа текущего месяца долг равен 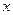, а 15-го числа предыдущего месяца долг равен . Тогда в конце предыдущего месяца долг равен и поэтому выплата в первой половине текущего месяца равна – .

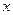Значит, в процентах от суммы кредита выплаты в феврале составили %, в марте составили 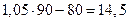%, в апреле – 14%, в мае – 13,5%, в июне – 13%, а в июле 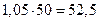%. Следовательно, общая сумма выплат составила %.

Ответ: 22,5.

Задача 3.

В июле планируется взять кредит в банке на сумму 28 млн рублей
на некоторый срок (целое число лет). Условия его возврата таковы:

— каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;

— с февраля по июнь каждого года необходимо выплатить часть долга;

— в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.

Чему будет равна общая сумма выплат после полного погашения кредита, если наибольший годовой платёж составит 9 млн рублей?

Решение 1. Пусть кредит планируется взять на лет. Долг перед банком (в млн рублей) по состоянию на июль должен уменьшаться до нуля равномерно:

28, , …, , , 0.

По условию, каждый январь долг возрастает на 25%, значит, последовательность размеров долга (в млн рублей) в январе такова:

35, , …, , .

Следовательно, выплаты (в млн рублей) должны быть следующими:

, , …, , .

Получаем: , откуда . Значит, всего следует выплатить

(млн рублей).

Ответ: 80,5 млн рублей.

Решение 2. По условию долг уменьшается по арифметической прогрессии:

.

Первая выплата равна 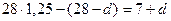. Вторая выплата равна , третья равна 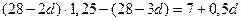, четвертая равна 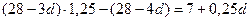и т.д. Значит, наибольшая выплата – первая, , выплат – 14 штук и они составляют арифметическую прогрессию, но с разностью .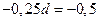

Общая выплата равна .

Ответ: 80,5 млн рублей.

Примеры оценивания решений заданий 17

Пример 1.

1 июня 2013 года Всеволод Ярославович взял в банке 900 000 рублей в кредит. Схема выплаты кредита следующая – 1 числа каждого следующего месяца банк начисляет 1 процент на оставшуюся сумму долга (то есть увеличивает долг на 1%), затем Всеволод Ярославович переводит в банк платёж. На какое минимальное количество месяцев Всеволод Ярославович может взять кредит, чтобы ежемесячные выплаты были не более 300 000 рублей?

Ответ: 4.

Комментарий.

Ответ верен. Более того «…построена математическая модель, решение сведено к исследованию этой модели…», см. критерии; в данном случае – арифметическая, числовая модель. Однако, эта модель построена неверно, т.е. она не соответствует условию. По решению видно, что сначала идет платёж долга, потом – начисление процента, а в условии – наоборот.