В случае декурсивного способа расчета сложных процентов, начисление на первоначальную сумму производится в конце периода наращения.
В конце первого периода наращенная сумма равна:
FV1 = PV + PV·i = P(1 + i).
В конце второго периода проценты начисляются на уже наращенную сумму
FV2 = PV(1+i) + PV(1+i)i = PV(1+i)(1+i) = P(1+i)2
и так далее, в конце n-ого периода наращенная сумма будет равна:
FVn = PV(1+i)n.
где FV – наращенная сумма;
i – годовая ставка сложных процентов;
n - срок ссуды;
(1+i)n - коэффициент наращения сложных процентов[12]
В практических расчетах в основном применяют дискретные проценты, то есть начисляемые за одинаковые интервалы времени (год, полугодие, квартал, месяц).
Задача
В кредитном договоре на сумму 1 000 000 руб. и сроком на 4 года, зафиксирована ставка сложных процентов, равная 20% годовых. Рассчитать наращенную сумму.
Решение
 руб.
руб.
Ответ: наращенная сумма FV = 2 073 600 руб.
Замечание
Величина FV существенно зависит от значений i и n. Например, будущая величина суммы всего в 1 рубль при годовой ставке 15% через 100 лет составит 1174313,45 (рисунок)

Рисунок 1. Наращение при сумме 1 рубль
Замечание
Если срок ссуды измеряется дробным числом лет, то наращенную сумму можно найти смешанным методом
S = P(1+i)[n](1+{n}i),
где [n] - целая часть числа n; {n}- дробная часть числа n.
Замечание
В случае, когда ставка сложных процентов меняется во времени (по полугодиям, кварталам, иногда помесячно), для начисления процентов используется формула:
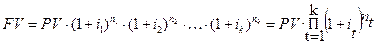 ,
,
где i1,i2,…,ik – последовательные значения ставок процентов, действующих в периоды n1,n2,…,nk.
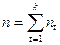 .
.
Если период меньше года (t), то наращенная сумма равна
 .
.
Наращение по сложным процентам антисипативным способом
При антисипативном способе начисления, проценты начисляются в начале каждого интервала. В договоре указывается изменяющаяся во времени базовая ставка (база) и размер надбавки к ней (маржи)[13].
Пусть годовая ставка сложных процентов j.
Число периодов начисления в году m.
При каждом начислении проценты капитализируются, то есть добавляются к сумме с начисленными в предыдущем периоде процентами. Каждый раз проценты начисляются по ставке j/m.
Ставка j – называется номинальной.
 ,
,
Где N – число периодов может быть и дробным N = mn.
Задача
Ссуда в 30 000 000 руб. предоставлена на 18 месяца. Проценты сложные, ставка 40% годовых. Проценты начисляются ежеквартально (раз в 3 месяца). Рассчитать наращенную сумму.
Решение
Число периодов начислений по договору  кварталов.
кварталов.
Число периодов начисления в году m = 4.
 руб.
руб.
Ответ: наращенная сумма FV = 53146830 руб.
Замечание
Если срок ссуды измеряется дробным числом лет, а начисление процентов производится m раз в году, то наращенная сумма может быть определена по смешанному методу
 ,
,
где ml - число полных периодов начисления процентов,
 - дробная часть одного периода начисления процентов.
- дробная часть одного периода начисления процентов.
Задача
На сумму 600 руб. ежеквартально по ставке 4% годовых начисляются сложные проценты в течение 14 месяцев. Определите величину наращенной суммы двумя методами.
Решение
Общее число периодов начисления процентов по договору составит:  , тогда имеем:
, тогда имеем:
ml = 4,  .
.
По стандартной формуле наращенную сумму найти сложно.
 руб.
руб.
Используя смешанный метод начисления, наращенная сумма составит:

 руб.
руб.
Ответ: FVстанд = 628,52 руб. FV смеш = 6288,53 руб.
Эффективная ставка
Часто возникает необходимость сравнения условий финансовых операций, предусматривающих различные периоды начисления процентов. В этом случае осуществляют приведение соответствующих процентных ставок к их годовому эквиваленту.
Если проценты капитализируются m раз в год, каждый раз со ставкой j/m, то, по определению, можно записать следующее равенство для соответствующих множителей наращения:
 ,
,
где EPR – эффективная ставка [effective percentage rate];
j – номинальная ставка.
Отсюда:
 или
или 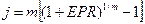
Опр. Эффективная ставка EPR – это годовая ставка сложных процентов, которую необходимо установить, чтобы получить такой же финансовый результат, как и при m разовом начислении процентов в году по ставке j /m.
Задача
Вычислить эффективную ставку процента, если банк начисляет проценты ежеквартально, исходя из номинальной ставки 10% годовых.
 .
.
Таким образом, условия помещения суммы на депозит под 10% годовых при ежеквартальном начислении процентов и под 10,3813%, начисляемых раз в год, являются эквивалентными.
Определить, какой должна быть номинальная ставка при ежеквартальном начислении процентов, чтобы обеспечить эффективную ставку 12% годовых.
 .
.
Таким образом, условия помещения суммы на депозит под 11,495% ежеквартально и под 12% годовых, являются эквивалентными.
Дисконтирование
Опр. Дисконтирование представляет собой процесс нахождения величины на заданный момент времени по ее известному или предполагаемому значению в будущем.
В экономическом смысле величина PV, найденная в процессе дисконтирования, показывает современное (с позиции текущего момента времени) значение будущей величины FV.
Дисконтирование, по сути, является зеркальным отражением наращения.
Если 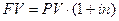 , то
, то  .
.
С помощью дисконтирования в финансовых операциях учитывается фактор времени.
На рисунке 2 приведена графическая диаграмма, отражающая процесс дисконтирования суммы в 1 рубль при различных ставках сложных процентов.

Рисунок 2. Дисконтирование суммы в 1 рубль при различных ставках
Как и следовало ожидать, величина PV также зависит от продолжительности операции и процентной ставки, однако зависимость здесь обратная - чем больше i и n, тем меньше текущая (современная) величина.
Опр. Дисконт - это разница между ценой, по которой покупатель покупает вексель или облигацию, и их номинальной стоимостью:
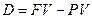 .
.
Опр. Расчет исходной суммы сделки (PV) по величине наращенной суммы (FV) называется дисконтированием суммы FV.
Опр. Величину PV, найденную дисконтированием наращенной суммы FV, называют современной стоимостью FV.
Опр. Процесс начисления и удержания процентов вперёд (в виде дисконтирования) называется учетом.
Опр. Учётная ставка [Discount rate - d] - это сумма, указанная в процентном выражении к величине денежного обязательства, которую взимает приобретатель обязательства. Это цена, взимаемая за приобретение обязательства до наступления срока уплаты[14].
Пусть d % - простая годовая учетная ставка;
d - относительная величина этой ставки;
Dг - сумма процентных денег за год;
D - сумма процентных денег за период, равный n,
тогда простая учетная ставка
 или
или 
FV - наращенная сумма.
Например, если облигация с номинальной стоимостью FV = 1000 рублей и сроком действия один год была приобретена за PV = 900 рублей, то учетная ставка d составила:
 .
.
Дисконт за 1 год: Dг = d×FV.
Дисконт за период n: D = n×Dг = n·d·FV.
Тогда наращенная сумма будет равна
FV = PV + D; FV = PV + n·d·FV;
FV - n·d·FV = PV;
Имеем:
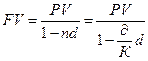 ,
,
А поскольку, на практике часто сталкиваются с задачей, обратной наращению процентов, когда по заданной сумме FV, которую следует уплатить через некоторое время n, необходимо определить исходной сумму PV, то
 .
.
Задача
Через 200 дней после подписания договора должник уплатит 350 руб. Кредит выдан под 15% годовых. Какова первоначальная сумма долга при условии, что при начислении процентов используется простая учетная ставка и временная база K=360 дням?
Решение
Первоначальная сумма долга - это величина PV;
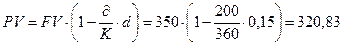 руб.
руб.
Ответ: РV = 320,83 руб.
Виды дисконтирования
Виды дисконтирования 
| |
| математическое | Банковский (коммерческий) учет |
| Решение задачи, обратной наращению первоначальной ссуды | Банк до наступления срока платежа по платёжному обязательству покупает его у владельца по цене ниже необходимой суммы и приобретает его с дисконтом. |
из  имеем имеем 
| Для расчета процентов применяется учетная ставка:
 то есть проценты за пользование ссудой начисляются на сумму, подлежащую уплате в конце срока ссуды. то есть проценты за пользование ссудой начисляются на сумму, подлежащую уплате в конце срока ссуды.
|
 - дисконтный коэффициент, который показывает какую долю составляет первоначальная сумма ссуды в окончательной величине долга.
где n - общий срок платежного обязательства. - дисконтный коэффициент, который показывает какую долю составляет первоначальная сумма ссуды в окончательной величине долга.
где n - общий срок платежного обязательства.
| Дисконт: 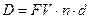 , откуда , откуда
 . .
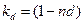 - дисконтный коэффициент.
n – измеряет период времени от момента учета векселя до даты его погашения[15]. - дисконтный коэффициент.
n – измеряет период времени от момента учета векселя до даты его погашения[15].
|
Дисконт при математическом дисконтировании: 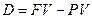 . .
| Дисконт при коммерческом учете: D = n·d·FV. |
Задача
Через 90 дней после подписания договора должник уплатит 1 000 000 руб. Кредит выдан под 20 % годовых (проценты обыкновенные). Какова первоначальная сумма и дисконт?
Решение
1) 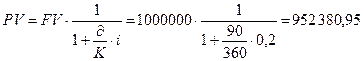 руб.
руб.
2)  руб.
руб.
Ответ: PV = 952380,95 руб. и D = 47 619,05 руб.
Задача
Через 90 дней предприятие должно получить по векселю 1 000 000 руб. Банк приобрёл его с дисконтом по учетной ставке 20% годовых (проценты простые и К=360). Определить полученную предприятием сумму и величину банковского дисконта.
Решение
1)  руб.
руб.
2) 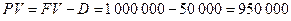 руб.
руб.
Ответ: D = 50 000 руб. и PV = 950 000 руб.
Задача
Вексель, выданный на 120 дней, с обязательством уплатить 50 тыс. руб., учитывается по ставке 8%. Определить приведенную величину наращенной стоимости и размер дисконта при математическом дисконтировании и коммерческом учете.
Решение
а) при математическом дисконтировании имеем:
1)  тыс. руб.
тыс. руб.
2)  тыс. руб.
тыс. руб.
б) при коммерческом учете имеем:
1)  тыс. руб.
тыс. руб.
2)  тыс. руб.
тыс. руб.
Ответ: а) PV = 48,70 тыс. руб. и D = 1,30 тыс. руб.
б) D = 1,33 тыс. руб. PV = 48,67 тыс. руб.
Задача
Владелец векселя номинальной стоимости 400 руб. и сроком обращения один год предъявил его банку - эмитенту для учета за 100 дней до даты погашения. Банк учел его по ставке 12% годовых (проценты простые). Определить дисконтированную величину и величину дисконта, временная база К=360.
Решение
1)  тыс. руб.
тыс. руб.
2)  тыс. руб.
тыс. руб.
Ответ: D = 13,33 тыс. руб. PV = 386,67 тыс. руб.
Замечание
В отдельных случаях может возникнуть ситуация, когда совмещают начисление процентов по ставке i и дисконтирование по ставке d. В этом случае наращенная величина ссуды будет определяться по формуле:
FV = PV(1+ni)(1-n¢×d),
где n - общий срок платежного обязательства;
n¢ - срок от момента учета обязательства до даты погашения долга, то есть n¢ ≤ n.
Задача
Долговое обязательство в сумме 2 000 руб. должно быть погашено через ∂ = 90 дней с процентами i = 10 % годовых. Владелец обязательства учел его в банке за  = 30 дней до наступления срока по учетной ставке d = 12 %. Найти полученную после учета векселя сумму.
= 30 дней до наступления срока по учетной ставке d = 12 %. Найти полученную после учета векселя сумму.
Решение
 руб.
руб.
Ответ FV = 2029,5 руб.