Проблема эквивалентности ставок в некоторых случаях может быть решена с помощью равенства средних значений ставок.
Начнем с простой ставки.
Пусть за периоды n1, n2,..., nm начисляются простые проценты по ставкам i1, i2,..., im на один и тот же капитал PV, тогда на основе равенства коэффициентов наращения:
,
получим искомую среднюю
,
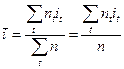здесь 
- общий срок наращения. Найденная характеристика представляет собой арифметическую среднюю взвешенную.
Аналогичнымспособомполучимсреднюю учетную ставку
.
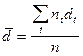Рассмотрим сложные ставки. Из равенства коэффициентов наращения
следует
.
Средняя в этом случае вычисляется как взвешенная средняя геометрическая.
Задача
Выданы две ссуды PV1 = 1 тыс. руб., PV2 = 2 тыс. руб. Первая выдана под 10 % годовых, вторая - под 15 %, сроки ссуд одинаковы и равны 2 годам.
Найти среднюю процентную ставку.
Решение
Найдем среднюю процентную ставку, если ставки простые
.
Средняя процентная ставка для сложных ставок
.
Рассмотрим случай, когда одновременно идет несколько однородных операций с разными ставками it и разными начальными суммами PVt, все суммы выданы на один и тот же срок n под простые проценты. Ответим на вопрос, под какую ставку надо поместить объединенную сумму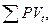 
чтобы получить тот же результат. Составляем уравнение эквивалентности
.
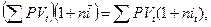
Искомая ставка равна взвешенной средней арифметической, в качестве весов берутся размеры ссуд.
Если проценты сложные, то уравнение эквивалентности будет выглядеть так
,
отсюда средняя ставка сложных процентов будет равна
.
Непрерывные проценты
В практических финансово-кредитных операциях непрерывные процессы наращения денежных сумм, т. е. наращения за бесконечно малые промежутки времени, применяются редко. Существенно большее значение непрерывное наращение имеет в количественном финансово-экономическом анализе сложных производственных и хозяйственных объектов и явлений, например, при выборе и обосновании инвестиционных решений. Необходимость в применении непрерывных наращений (или непрерывных процентов) определяется, прежде всего, тем, что многие экономические явления по своей природе непрерывны, поэтому аналитическое описание в виде непрерывных процессов более адекватно, чем на основе дискретных. Обобщим формулу сложных процентов для случая, когда проценты начисляются m раз в году:
|
|
Наращенная сумма при дискретных процессах находится по этой формуле, здесь m - число периодов начисления в году, j - годовая или номинальная ставка. Чем больше m, тем меньше промежутки времени между моментами начисления процентов. В пределе при m ®¥ имеем:
` 
.
Используя второй замечательный предел
- основание натурального логарифма.
Получаем:
,
И тогда: 
.
При непрерывном наращении процентов применяют особый вид процентной ставки - силу роста, которая характеризует относительный прирост наращенной суммы в бесконечно малом промежутке времени. При непрерывной капитализации процентов наращенная сумма равна конечной величине, зависящей от первоначальной суммы, срока наращения и номинальной ставки процентов. Для того, чтобы отличить ставки непрерывных процентов от ставки дискретных процентов, обозначим первую через d, тогда 
.
Дисконтирование осуществляется по формуле:
|
|
.
Опр. Сила роста d представляет собой номинальную ставку процентов при m®¥.[16]