Наращение по простым процентам
Опр. Индекс цен Ip показывает, во сколько раз выросли цены за рассматриваемый промежуток времени[17].
Пусть за рассматриваемый промежуток времени n, сумма денег составляет FV, то реально наращенная сумма денег с учетом их покупательской способности равна:
.
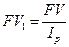Тогда стоимость потребительской корзины за исследуемый промежуток времени изменилась на величину 
.
Величина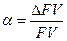 
называется темпом инфляции.
Тогда если величина 
называется индексом инфляции, то имеем
Если наращение производится по простой ставке в течение n лет, то реальное наращение при темпе инфляции a составит:
.
Наращение по сложным процентам
Наращенная по сложным процентам сумма к концу ссуды с учетом падения покупательской способности денег составит:
Пусть a - годовой темп инфляции.
S – сумма денег.
Для того, чтобы сохранилась покупательская способность, сумма S должна через один год составлять: 
через два года: 
через n лет: 
За рассматриваемый период (n лет) индекс инфляции (Iинф) при a = const составит 
,
В общем случае 
.
Таким образом, инфляционный рост цен подчиняется закону сложного процента.
Задача
Цены с 2000 по 2009 годы по данным Госкомстата РФ в Архангельской области[18] возрастали за каждый год на 13%. Найдите темп инфляции за исследуемые 10 лет.
Решение
По условию, годовой темп инфляции a = 0,13.
Тогда индекс цен за год
Следовательно за исследуемые 10 лет темп инфляции составил:
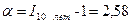
Задача
По данным Госкомстата РФ в Архангельской области цены с 2000 по 2009 годы изменяли так как показано в таблице №1. Найдите темп инфляции за исследуемые 10 лет.
Таблица №1
| Год (t) | ||||||||||
| Темп роста инфляции к декабрю предыдущего года; в процентах (α) | 0,21 | 0,20 | 0,16 | 0,13 | 0,13 | 0,10 | 0,09 | 0,13 | 0,14 | 0,09 |
Решение
|
|
Следовательно за исследуемые 10 лет темп инфляции составил:
.
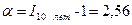Инфляционная премия
Для экономик многих стран характерны инфляционные процессы, поэтому их необходимо учитывались в финансовых расчетах. Процентная ставка, которая при начислении простых процентов компенсирует инфляцию, может быть определена как:
.
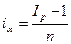Один из способов компенсации обесценивания денег заключается в увеличении ставки процентов на величину, называемую инфляционной премией. Скорректированная таким образом ставка называется брутто ставкой ia.
Пусть i - безинфляционная ставка, отражающая реальную доходность операции;
ia - процентная ставка, которая учитывает инфляцию.
Тогда наращенная сумма S на первоначальный капитал P за год составит
FV = PV(1+ ia) или FV = PV(1+i)(1+a),
отсюда
(1+ ia) = (1+i)(1+a) и ia = i+a+ia - формула Фишера.
Годовую ставку i, чтобы учесть инфляцию, нужно увеличить на величину a+ia, эта величина называется инфляционной премией.
Опр. Инфляционная премия - часть номинальной ставки процента, отражающая ожидаемый уровень инфляции.
Опр. Инфляционная премия [inflation premium]- это дополнительный доход, выплачиваемый (или предусмотренный к выплате) предприятию контрагентом по финансовым операциям с целью возмещения его потерь от обесценивания денег в связи с инфляцией. Уровень его рассчитывается исходя из темпа инфляции в рассматриваемом периоде[19].
Выводы:
1) если ставка сложных процентов, в которую вложена инфляция, равна темпу инфляции ia =a, то реальная доходность операции равна 0;
|
|
2) если ia < a, то i < 0, финансовая операция убыточна;
3) если ia > a, то i > 0, финансовая операция приносит реальный доход.
В случае, если период n отличен от одного года, для простых ссудных процентов мы имеем
откуда 
.
Для сложных процентов
(1+ ia)n = (1+i)n × Iи,
Отсюда ставка сложных процентов, учитывающая инфляцию
ia =(1+i)× 
.
Задача
Кредит 12 000 руб. выдан на 3 года. На этот период прогнозируется рост цен в 2,2 раза. Определить ставку процентов при выдаче кредита и наращенную сумму долга, если реальная доходность должна составлять 12 % годовых по ставке сложных процентов.
Решение
Нам нужно найти ставку сложных процентов, учитывающую инфляцию
ia =(1+i)× = (1+0,12)× 
= 0,4566 (45,66 %).
Наращенная сумма долга составит
FVa =12 000(1+0,4566)3 = 37 085,3 руб.
Найдем номинальную ставку сложных процентов, учитывающую инфляцию
,
выполнив преобразования, получим
- 1.
Задача
При уровне инфляции 80 % в год капитал вкладывается на один год под номинальную ставку 50 %, начисление процентов ежемесячное. Какова реальная доходность этой операции.
Решение
По условию n=1, m=12, a =0,8, I=1,8, ja =0,5. Нам нужно найти безинфляционную номинальную ставку сложных процентов, чтобы оценить реальную доходность операции. Из уравнения
находим j:
- 1 = 12 × 
.
Вывод: финансовая операция убыточна.