Математический учет
В этом случае решается задача обратная наращению по сложным процентам
Имеем:
, откуда:
где
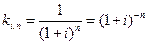- дисконтный коэффициент.
Величина дисконта
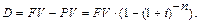
При начислении процентов m раз в году получим
,
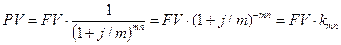где 
- дисконтный коэффициент.
Величина дисконта
.
Так же как и в случае начисления простых процентов, величину PV, полученную дисконтированием FV называют современной или текущей стоимостью или приведенной величиной FV.
Банковский учет
В этом случае предполагается использование сложной учетной ставки.
Имеем:
,
Где dсл – сложная годовая учетная ставка.
Величина дисконта
.
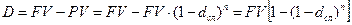При дисконтировании m раз в году используется номинальная ставка f:
,
Величина дисконта
.
Задача
Через 4 года предприятию будет выплачена сумма 1 000 000 000 руб. Определить её современную стоимость, при условии, что применяется ставка сложных процентов – 10% годовых.
Решение
руб.
Ответ: 683 013,5 руб.
Задача
Через 4 года предприятию будет выплачена сумма 1 000 000 000 руб. Определить её современную стоимость, при условии, что на первоначальную сумму начисляются сложные проценты по 8% годовых ежеквартально.
Решение
руб.
Ответ: 728 445,8руб.
Задача
Через 4 года по векселю должна быть выплачена сумма 1 000 000 000 руб. Банк учел вексель по сложной учетной ставке 10% годовых. Определить дисконт.
Решение
руб.
руб.
Ответ: 343 900 руб.
Задача
Через 4 года по векселю должна быть выплачена сумма 1 000 000 000 руб. Банк учел вексель по сложной учетной ставке 8% годовых при m = 4. Определить дисконт.
Решение
руб.
руб.
Ответ: 276 202,3руб.
Эквивалентный переход от одной ставки к другой
В связи с тем, что договоры могут быть составлены с использованием различных видов ставок, для сопоставления их доходности возникает необходимость в установлении правил эквивалентности приведения различных ставок к ставке одного вида.
|
|
Опр. Ставки, обеспечивающие равноценность последствий финансовых операций, называются эквивалентными.
Для того, чтобы установить эквивалентность между простой ставкой наращения I и учетной ставки. Формулы учетной ставкой дисконтирования d, воспользуемся формулами:
; 
.
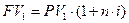Наращенные суммы и капиталы равны, то есть FV1 = FV2 и PV1 = PV2. Тогда равны будут и коэффициенты наращения:
Отсюда получаем две формулы эквивалентного перехода
.
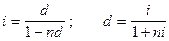Соотношения между этими ставками зависят от срока n,
Две формулы верны, когда временные базы (К) равны.
Замечание
Если же начисление процентов по ставке i производится при К = 365 дней, а по ставке d при К = 360 дней, то легко доказать, что формулы эквивалентности принимают вид:
,
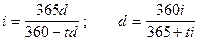где t = ¶ (дни).
Задача
Вексель учтен в банке по учетной ставке 8 % в день окончания срока его обращения, равного 200 дням (К=360). Определить доходность этой операции по ставке простых процентов (К = 365).
Решение
Эквивалентная ставка простых процентов, которая даст тот же финансовый результат, что и учетная ставка, составит:
.
При расчете эквивалентности ставок следует иметь в виду, что для каждого периода наращения необходимо рассчитать свою эквивалентную ставку.
Рассмотрим эквивалентность простой и сложных процентных ставок при начислении процентов один раз в год.
Приравняем коэффициенты наращения
.
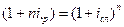Отсюдаследует, что
.