ГЛАВА 5. СИНТЕЗ ЦИФРОВЫХ РЕГУЛЯТОРОВ ДЛЯ
ЭЛЕКТРОМЕХАНИЧЕСКИХ СИСТЕМ
Общие сведения
Из-за необходимости преобразования информационных управляющих сигналов из аналоговой формы в цифровую и наоборот, а также из-за необходимости их квантования во времени структура цифровых систем управления содержит следующие элементы (на рис5.1 показана структура цифровой системы регулирования тока якоря):
ИЭ – импульсный элемент, выполняющий функции амплитудно-импульсного модулятора. ИЭ периодически через интервал времени Т 0 замыкается на короткое по сравнению с Т 0 время;
D Т(z) – цифровой фильтр или цифровой регулятор, осуществляющий функцию управления;
W Э(p) – экстраполятор нулевого порядка, преобразующий цифровой код регулятора в аналоговое напряжение, постоянное по величине на одном периоде дискретности Т 0;
W Н (р) – неизменяемая (аналоговая) часть системы или контура регулирования одной из координат электропривода;
W АЦП (р) – аналого-цифровой преобразователь, преобразующий сигнал аналогового датчика обратной связи в цифровую форму [5,6];
N З, NT – задающий и сигнал обратной связи по регулируемой координате в цифровой форме.
Синтез регуляторов контура тока
Дискретная передаточная функция (ДПФ) неизменяемой части системы в контуре тока может быть получена на основе передаточной функции аналоговой части системы с учетом возникающих запаздываний в передаче управляющего воздействия. Время запаздывания τ вызвано конечной скоростью выполнения вычислений микроЭВМ заданного алгоритма расчета угла отпирания тиристоров. Рассмотрим нахождение ДПФ неизменяемой части системы без учета влияния противо-ЭДС двигателя постоянного тока (ДПТ) и инерционных свойств силового тиристорного преобразователя
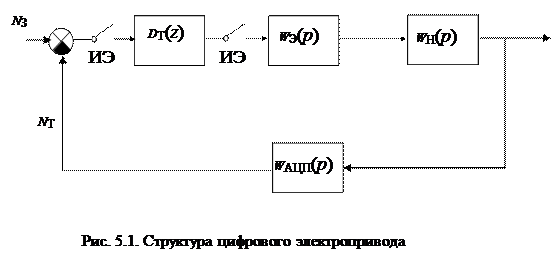 |
Рассмотрим контур регулирования (рис. 5.1), в котором ток якоря ДПТ усредняется за период дискретности T 0 с помощью интегрирующего АЦП, работа которого синхронизируется с моментами естественного отпирания тиристоров в тиристорном преобразователе (ТП) [7]. В момент естественной коммутации тиристоров поступает информация о текущей величине тока в микроЭВМ. Спустя время t1, затрачиваемое на вычисления в микроЭВМ, выдается новое значение угла отпирания тиристора α1,, отсчитываемое от точки естественной коммутации. Если wt1 < a1, где w = 2p f – круговая частота сети, то запаздывание отсутствует, если же wt1 > a1, то появляется запаздывание на один такт [21].
ДПФ неизменяемой части контура тока для этого случая может быть найдена с учетом экстраполятора нулевого порядка из соотношения:
 , (5.1)
, (5.1)
где К П – коэффициент передачи тиристорного преобразователя; К ДТ – коэффициент передачи датчика тока; b = 0 или 1 в зависимости от заданного a1; γ = t1/ Т 0 – относительное время запаздывания микроЭВМ; R Э, T Э – эквивалентные сопротивление и постоянная времени цепи якоря ДПТ с учетом параметров силового преобразователя.
В результате преобразований получим:
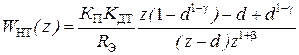 , (5.2)
, (5.2)
где d = exp (- Т 0/ Т Э).
Разлагая d 1-γ в ряд Тейлора и ограничиваясь двумя членами ряда, окончательно определим:
 . (5.3)
. (5.3)
Таким образом, ДПФ непрерывной части контура тока оказывается переменной, что затрудняет синтез регулятора тока. Поэтому на практике прибегают к вводу управляющей информации в ТП в момент следующего естественного отпирания, т.е. полагают b = 1. В этом случае ДПФ имеет вид:
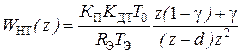 . (5.4)
. (5.4)
В случае питания якоря ДПТ от широтно-импульсного преобразователя (ШИП) ДПФ неизменяемой части системы в контуре тока без учета противо-ЭДС может быть определена из выражения:
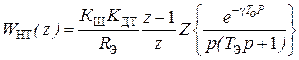 , (5.5)
, (5.5)
где К Ш – коэффициент передачи ШИП, γ Т 0 – время запаздывания, вносимое микроЭВМ в процессе расчета алгоритма управления. Продолжая преобразования, найдем 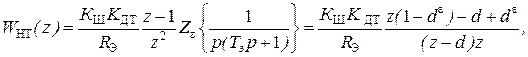
где d = exp (– Т 0/ Т Э), e = 1–γ.
Выполняя преобразования, аналогичные выше рассмотренному случаю, определим:
 . (5.6)
. (5.6)
По найденной ДПФ неизменяемой части контура тока вычислим за счет подстановки  дискретную частотную характеристику (ДЧХ):
дискретную частотную характеристику (ДЧХ):
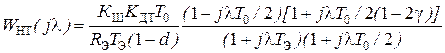 , (5.7)
, (5.7)
где j – мнимая единица, λ – абсолютная псевдочастота [2].
Найденную ДЧХ можно получить на основе описанных в [5,21] правил. Например, для непрерывной части контура тока без учета запаздывания с передаточной функцией  ДЧХ имеет вид:
ДЧХ имеет вид:
 , где К – коэффициент передачи контура тока.
, где К – коэффициент передачи контура тока.
Определим ДПФ цифрового регулятора тока, воспользовавшись описанным в [2] методом логарифмических амплитудно-частотных характеристик (ЛАЧХ). Для этого следует задать желаемую ДЧХ разомкнутой системы, равную:
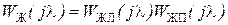 , (5.8)
, (5.8)
где  – ДЧХ левая, включающая большие и средние постоянные времени, имеющие частоты сопряжения меньше частоты среза λС,
– ДЧХ левая, включающая большие и средние постоянные времени, имеющие частоты сопряжения меньше частоты среза λС, 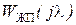 – ДЧХ правая, содержащая малые постоянные времени неизменяемой части контура тока справа от частоты среза, λС – псевдочастота среза системы [6]. Полная ДЧХ рассматриваемого контура тока равна:
– ДЧХ правая, содержащая малые постоянные времени неизменяемой части контура тока справа от частоты среза, λС – псевдочастота среза системы [6]. Полная ДЧХ рассматриваемого контура тока равна:
 . (5.9)
. (5.9)
Так как разность порядков числителя и знаменателя  равна 1, то ДЧХ регулятора тока будет иметь вид:
равна 1, то ДЧХ регулятора тока будет иметь вид:
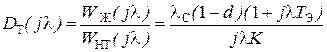 , (5.10)
, (5.10)
где 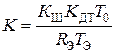 . Определим ДПФ регулятора тока, выполнив подстановку
. Определим ДПФ регулятора тока, выполнив подстановку 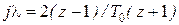 и необходимые преобразования:
и необходимые преобразования:
 , (5.11)
, (5.11)
где С 1 = Т Э/ Т 0.
Для расчета параметров регулятора тока следует определить частоту среза lС, обеспечивающую требуемые показатели переходного процесса в контуре тока, из условия: lС = 1/(аТ å), где Т å – сумма малых постоянных времени неизменяемой части контура, а – параметр, определяющий величину перерегулирования s.
Для рассматриваемого случая Т å = 0,5 Т 0 + γ Т 0, величина a выбирается из табл. 1, например, для s = 0,08 примем а = 1,75.
Таблица 1
| a | 2,5 | 2,0 | 1,75 | 1,5 | 1,25 | 1,00 | 0,75 | 0,5 |
| s | 0,01 | 0,04 | 0,08 | 0,13 | 0,21 | 0,32 | 0,45 | 0,7 |
При применении в качестве силового преобразователя ТП с усредняющим за период дискретности датчиком тока ДПФ неизменяемой части контура тока имеет вид:
 , (5.12)
, (5.12)
а соответствующая ей ДЧХ:
 (5.13)
(5.13)
отличается от раннее рассмотренной на множитель z -1, то есть имеет дополнительное запаздывание на один такт. ДПФ регулятора тока отличается от полученной выше тем, что Т å=0,5 Т 0+γ Т О+ Т О. Указанное отличие приводит к другим параметрам регулятора.
Пример расчета 1. Рассчитаем параметры регулятора тока для ДПТ типа ПБСТ-53, питающегося от ТП, выполненного по трехфазной нулевой схеме. Для измерения тока якоря используем датчик с усреднением за период дискретности. Параметры неизменяемой части контура тока: Р Н = 6 кВт; U Н = 220 В; I Н = 30 А; Т Э = 0,0188 с; R Э = 0,177 Ом; Т М = 0,0204 с; Т 0 = 0,0066 с; К П = 20; К ДТ = 0,066 Ом; γ = 0,3.
ДПФ регулятора тока для этого случая имеет вид:
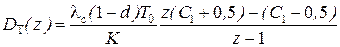 .
.
Определим:  ,
, 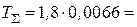 =0.0118 с. Из табл.1 выберем а = 1,5, что соответствует s = 0,13, и рассчитаем:
=0.0118 с. Из табл.1 выберем а = 1,5, что соответствует s = 0,13, и рассчитаем: 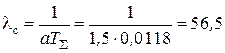 с –1.
с –1.
Определим: 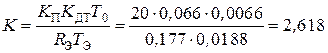 ,
,  ,
, 
Окончательно ДПФ регулятора тока равна:
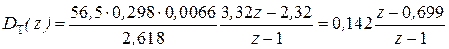 .
.
Пример расчета 2. Рассчитаем параметры регулятора тока для ДПТ типа ДК1-3,5, питающегося от ШИП. Для измерения тока якоря используется датчик мгновенного значения тока. Параметры неизменяемой части контура регулирования: Р Н = 0,37 кВт; U Н = 60 В; I Н = 7,5 А; R Э = 1,2 Ом; Т Э = 0,005 с; Т М = 0,018 с; Т 0 = 0,001 с; К Ш = 7; К ДТ = 0,6 Ом; γ = 0,4.
ДПФ регулятора тока для этого случая имеет вид:
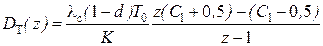 , где
, где 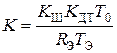 .
.
Вычислим: 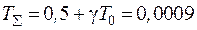 с, из табл.1 выбираем а = 2 и определяем частоту среза lС:
с, из табл.1 выбираем а = 2 и определяем частоту среза lС: 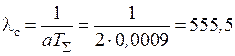 с-1, а затем вычислим
с-1, а затем вычислим
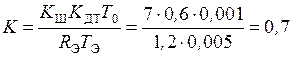 ,
, 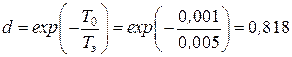 ,
, 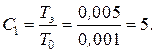
Окончательно получим ДПФ регулятора тока:
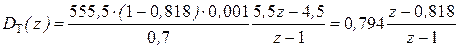 .
.
Применение в электроприводе высокомоментных ДПТ, имеющих близкие по величине электромагнитную и электромеханическую постоянные времени, требует учета влияния противо-ЭДС на статические и динамические характеристики контура регулирования тока [12]. Для этого применим более сложную передаточную функцию ДПТ по управляющему воздействию относительно тока якоря:
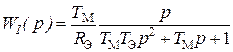 ,
,
где Т М– механическая постоянная времени электропривода.
Определим ДЧХ с учетом того, что Т М > T 0 и Т Э > T 0. В области низких частот ДЧХ определяется нулями и полюсами, лежащими слева от частоты среза 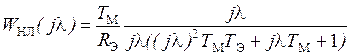 .
.
В области высоких частот с учетом запаздывания микро-ЭВМ, равного gТ0, ДЧХ имеет вид:
 .
.
Примем желаемую ДЧХ контура тока с учетом необходимости получения астатизма первого порядка следующего вида 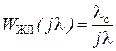 , а
, а 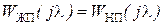 , тогда ДЧХ регулятора тока определится выражением:
, тогда ДЧХ регулятора тока определится выражением: 
Для нахождения ДПФ регулятора тока сделаем подстановку 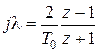 и после некоторых преобразований получим:
и после некоторых преобразований получим:
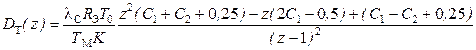 , (5.14)
, (5.14)
где К = К П К ДТ,  ,
, 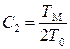 .
.
Пример расчета 3. Рассчитаем параметры регулятора тока для условий примера расчета 2.