Структура неизменяемой части цифрового электропривода показана на рис.7. В ней скомпенсировано влияние нелинейностей тиристорного преобразователя и введена положительная обратная связь по скорости двигателя, компенсирующая противо-ЭДС. Неизменяемая часть ЦЭП описывается следующими передаточными функциями [12]:
1)передаточная функция W Ф(р) соответствует формирователю тока, её вид зависит от типа преобразователя и режима его работы:
2)передаточная функция 
описывает электромеханическую часть электропривода;
3)передаточная функция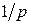 
характеризует связь между скоростью двигателя и углом поворота его вала;
Таблица 2
ДПФ регулятора и корректирующего звена в контуре регулирования скорости для азличных вариантов исполнения системы регулирования
| Порядок | Полиномы | ДПФ регулятора и корректирующего звена | ДПФ разомкнутой и замкнутой системы | ||||
| R | M 1(z) | N 1(z) | P (z) | D C(z) | W Д(z) | W (z) | Ф(z) |
| 
| 
| 
| - | 
| 
| |
|
| 
| 
| 
| 
| 
|
| |
| 
| 
| 
| 
| 
| 
| |
| 
| 
| 
| - | 
| 
| |
|
| 
| 
| 
| 
| 
| |
|
|
|
| 
| 
| 
|
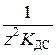
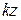
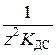
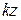
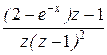
Датчики скорости и тока совместно с интегрирующим АЦП описываются передаточными функциями 
 |
.
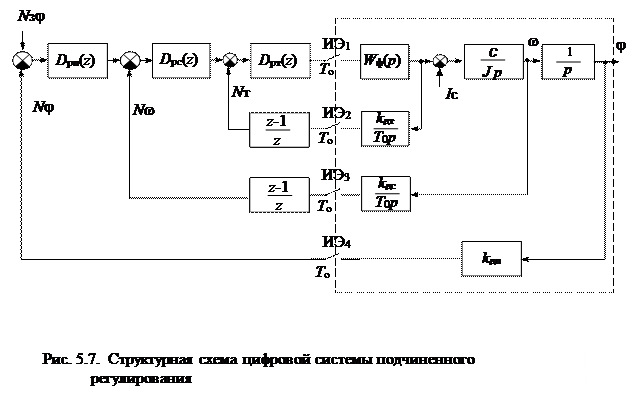Датчики положения - пропорциональный с коэффициентом передачи 
. Периоды переключения ключей 
в общем случае могут быть разными, но принимаются в дальнейших выводах одинаковыми и равными 
.
Передаточная функция формирователя тока для тиристорного преобразователя в РНТ равна в относительных единицах
,
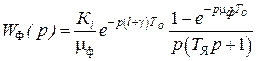где 
- коэффициент передачи по току; 
- относительная длительность фазы; 
- целая часть запаздывания; 
- дробная часть запаздывания;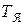 
- эквивалентная постоянная времени цепи якоря.
Формирователь тока с широтно-импульсным преобразователем имеет передаточную функцию 
, где l =0, mф =1. Передаточная
функция формирователей может быть записана в общем виде
. (5.37)
Если принять периоды дискретности в контурах тока, скорости и положения
в структуре (рис.7) электропривода равными периоду квантования Т0, то передаточная функция неизменяемой части системы примет вид
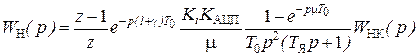, (5.38)
где W НК(p) – передаточная функция непрерывной части контура регулирования
учёта формирователя тока.
Определим дискретную частотную характеристику неизменяемой части
контура регулирования, подвергнув W н(р) модифицированному z – преобразованию 
, билинейному преобразованию вида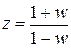 
и подстановке 
, учитывая что
, 
, (5.39)
; 
,
окончательно получаем
, (5.40)
где q 1 и q 2 характеризуют эквивалентное запаздывание неизменной части объекта регулирования. Полученное выражение является приближённым, но достаточно хорошо учитывает переменный характер запаздывания. ДЧХ удобно представить в виде:
, (5.41)
где 
– ближайшее сверху целое число к наибольшему из значений q 1 и q 2. Обычно на практике принимают N равным 1 или 2. При условии компенсации влияние противо-ЭДС, оговорённом выше, ДЧХ неизменяемой части электропривода в различных контурах имеют вид:
1) для контура тока при 
:
; (5.42)
2) для контура скорости при отсутствии контура тока
; (5.43)
3) для контура положение при отсутствии подчинённых контуров скорости и тока.
, (5.44)
где К НТ, К НС, К НП – соответственно коэффициенты передачи контуров тока, скорости и положения.
Синтез компенсационных регуляторов осуществляется на основе заданной желаемой ДЧХ замкнутого контура регулирования
, (5.45)
где 
– ДЧХ, обеспечиваются заданное распределение корней характеристического полинома замкнутой системы.
Для обеспечения требуемых показателей переходного процесса и придания замкнутому контуру астатизма первого или второго порядка стандартная форма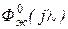 
задаётся ДЧХ определённого вида [13].
ДЧХ неизменяемой части контура без учёта запаздывания имеет вид:
, ДЧХ регулятора определяется следующим выражением: 
Для практической реализации регулятора целесообразно использовать его ДПФ, так как её коэффициенты представляют коэффициенты регулятора во временной области. ДПФ регулятора находится из выражения
(5.46)
Переход от ДЧX регулятора к его ДПФ можно осуществить либо табличным способом, либо путём замены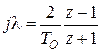 
.