Передаточных функций
Во многих случаях применения регулируемого контура тока обеспечивает ограничение максимального допустимого тока якоря ДПТ, например, в подчиненных системах регулирования [25]. В этих случаях целесообразно обеспечить апериодический характер изменения тока без перерегулирования, что гарантирует эффективное ограничение тока в переходных режимах.
Желаемая ДПФ замкнутого контура тока может быть определена из следующих рассуждений [7]. Выходной сигнал для такой системы, представленный в виде решетчатой функции, имеет вид  (функция имеет относительное представление по отношению к I max). Простое z – преобразование этой функции, взятое из таблиц, равно:
(функция имеет относительное представление по отношению к I max). Простое z – преобразование этой функции, взятое из таблиц, равно:
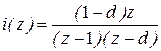 , где
, где  .
.
С учетом того, что этот сигнал является реакцией замкнутой системы с ДПФ ФЖ(z) на единичный ступенчатый сигнал 1[ п ] с ДПФ z /(z -1), можно записать:
 , откуда вытекает, что
, откуда вытекает, что 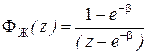 .
.
ДПФ разомкнутой системы при единичной обратной связи:
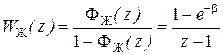 . (5.21)
. (5.21)
При известной ДПФ неизменяемой части контура тока 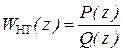 , где P(z), Q(z) – соответственно числитель и знаменатель передаточной функции, ДПФ последовательного включенного цифрового фильтра (регулятора), обеспечивающего апериодический переходной процесс, равна:
, где P(z), Q(z) – соответственно числитель и знаменатель передаточной функции, ДПФ последовательного включенного цифрового фильтра (регулятора), обеспечивающего апериодический переходной процесс, равна:
 . (5.22)
. (5.22)
Выполним синтез регулятора тока для случая, когда в системе отсутствует запаздывание. В этом варианте ДПФ неизменяемой части системы
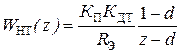 , где
, где  .
.
Для получения апериодического переходного процесса примем ДПФ разомкнутого контура 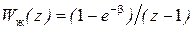 , тогда ДПФ регулятора тока будет равна:
, тогда ДПФ регулятора тока будет равна:
 , где
, где  .
.
Регулятор тока имеет структуру ПИ – регулятора.
Применим рассмотренную методику для синтеза регулятора тока при наличии временного запаздывания g Т 0, вносимого микроЭВМ. ДПФ непрерывной части контура тока, как было показано выше, равна:
 .
.
Выполняя соответствующие преобразования, получим ДПФ регулятора тока:
 . (5.23)
. (5.23)
Пример расчета 6. На основе исходных данных примера 2, задавшись g = 0,6, рассчитаем параметры регулятора тока. Из предыдущего примера расчета известно, что d = 0,701; е – β = 0,549, вычислим
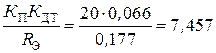 .
.
Следовательно, ДПФ регулятора тока:
 .
.
Пример расчета 7. По исходным данным примера расчета 2, задавшись β = 0,6 и g = 0,3 (относительное запаздывание микроЭВМ), рассчитаем параметры регулятора тока. Выполнив расчеты: найдем ДПФ регулятора тока: 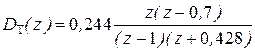 .
.
Рассмотрим синтез регулятора тока в условиях учета противо-ЭДС ДПТ. ДПФ неизменяемой части контура тока включает в себя для этого случая ДПФ ДПТ по управляющему воздействию относительно тока якоря, а также коэффициенты передачи силового преобразователя и датчика
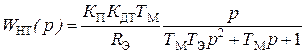 .
.
Подвергая эту передаточную функцию z- преобразованию, получим:
 ,
,
где  ,
, 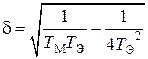 ,
,  ,
,  .
.
С учетом того, что желаемая ДПФ разомкнутого контура тока равна
 , определим ДПФ регулятора тока:
, определим ДПФ регулятора тока:
 . (5.24)
. (5.24)
Пример расчета 8. Определим ДПФ регулятора тока и его параметры с учетом противо-ЭДС ДПТ для исходных данных примера 2. Вычислим:
 ,
,  ,
,  ,
,  и находим
и находим
 Можно определить ДПФ регулятора тока и с учетом запаздывания в микро-ЭВМ, но при этом получается ДПФ регулятора тока третьего порядка, что может затруднить ее реализацию. В связи с тем, что запаздывание в контуре тока обычно принимают равным одному периоду дискретности можно обойтись и рассмотренной ДПФ регулятора тока, если применить компенсацию запаздывания.
Можно определить ДПФ регулятора тока и с учетом запаздывания в микро-ЭВМ, но при этом получается ДПФ регулятора тока третьего порядка, что может затруднить ее реализацию. В связи с тем, что запаздывание в контуре тока обычно принимают равным одному периоду дискретности можно обойтись и рассмотренной ДПФ регулятора тока, если применить компенсацию запаздывания.