Взаимосвязанные механические подсистемы

Если в многомассовой упругой механической подсистеме, уп­равление которой осуществляется многодвигательными электропри­водами, в явном виде отсутствуют звенья с распределенными пара­метрами, то механическая подсистема может быть представлена в виде многих элементов с сосредоточенными массами, соединенных между собой безмассовыми упругими связями. Под действием не­скольких входных переменных ВМП будет совершать основное дви­жение и колебательные движения относительно основного. Колеба­ния ВМП всегда являются затухающими из-за влияния восстанав­ливающих сил системы, поэтому математическое описание ВМП сле­дует выполнять с учетом этих сил. Однако делать это можно только для простых случаев или после упрощения исходной модели систе­мы, в связи с тем, что полная математическая модель ВМП может оказаться сложной и обращение с нею в задачах анализа и синтеза взаимосвязанных систем управления станет практически невозмож­ным. Поэтому целесообразно вначале составить детализированное математическое описание ВМП без учета демпфирующих сил, вы­полнить ее упрощение таким образом, чтобы с достаточной точнос­тью отразить динамические свойства системы в заданных полосах частот сепаратных подсистем, а затем уже в упрощенных моделях учесть силы демпфирования.

К механическим системам с сосредоточенными параметрами мо­гут быть приведены и системы с распределенными параметрами.

При исследовании ВМП возникают следующие задачи:

1) определения структуры механической модели ВМП, обеспечи­вающей при т входных и r выходных переменных оптималь­ное решение задачи управления ВЭМП;

2) анализа и синтеза ВМП, в соответствии с которыми на стадии проектирования находятся такие сочетания инерционно-жесткостных и демпфирующих параметров, которые обеспечивали бы малую интенсивность колебаний механизма в заданных по­лосах частот сепаратных подсистем управления. Рассмотрим наиболее общий вариант ВМП, при котором отдель­ные элементы системы имеют несколько степеней свободы. Диффе­ренциальные уравнения, характеризующие свободные колебания та­кой ВМП, могут быть получены из уравнений Лагранжа:

(13.13)

Раскрытие уравнения (13.13) относительно Т и П приводит к системе однородных линейных дифференциальных уравнений вто­рого порядка

, (13.14)

где q - k -вектор обобщенных координат;М, С — симметричные квадратные матрицы соответственно коэффициентов инерции и коэффициентов жесткостей ().

По полученным таким образом дифференциальным уравне­ниям целесообразно составить структуру механической модели, которую в дальнейшем удобно использовать для анализа и синте­за ВМП.

Подставляя частные решения в уравнение (13.14), получим:

,

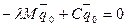где - k -вектор относительных амплитуд свободных колеба­ний .

Переписав это уравнение в виде:

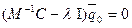, (13.15)

где I -единичная матрица, можем определить вектор как собствен­ный вектор матрицы , а 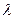как ее собственные значения.

Для многих вариантов механизмов уравнение (13.15) может быть записано в более простом виде

, (13.16)

где .

Собственные значения матрицы G определяют соб­ственные частоты колебаний механической подсистемы. Решение уравнения (13.16) для каждого из найденных дает собственные век­тора матрицы G, имеющие важное значение при исследовании ди­намики ВМП. Соотношение относительных амплитуд колебаний элементов механической системы в теоретической механике иллю­стрируется графически в виде форм колебании. Однако они не дают однозначного ответа о преимущественной принадлежности интере­суемой частоты колебаний к тому или иному элементу ВМП. Такую информацию можно получить, если совместно с формами колебаний рассматривать для каждой 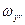и распределение относительных зна­чений потенциальной энергии, запасаемой в упругих звеньях , где - относительное значение потенци­альной энергии, запасаемой в упругом звене при - относительные амплитуды колебаний i -го и j -го инерционных зве­ньев. Тогда можно точно установить принадлежность каждой час­тоты колебаний элементам ВМП, что важно в задачах синтеза при варьировании инерционно-жесткостных параметров для получения заданных частот колебаний.

Линеаризованные модели ЭМС. Для математического описа­ния механической подсистемы в составе системы управления при линейном приближении необходимо знать передаточную матрицу, связывающую выходные и входные переменные. Такая матрица мо­жет быть определена либо через уравнение состояния, либо непос­редственно по дифференциальным уравнениям, составленным для известной структуры механической модели в виде:

.

Резольвента матрицы А может быть определена, если записать:

;

,

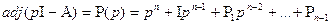где - характеристический многочлен системы; - присое­диненная матрица.

Коэффициенты , и матрицы , вычисляются в соответствии с алгоритмом Фадеева-Леверье.

Выполнив подстановки и в выражении (13.17), по­лучим

,

где ; .

Передаточная матрица W(р) представляет собой полиномиаль­ную матрицу, элементами которой являются передаточные функции , между j -м выходом и s-м входом ,

,

где - j -я строка матрицы C; - s-й столбец матрицы.

Матрица А содержит коэффициенты, которые могут быть оп­ределены из системы уравнений, записанных на основании уравне­ний (13.16) с учетом дополнительных переменных и принятых обо­значений

.

Матрица В определяется правой частью уравнений (13.16), если записать их для вынужденных движений конкретной механи­ческой системы. В частности, если считать, что на каждый элемент механической модели действует обобщенная сила (рассматриваемая как входная переменная), а моменты сопротивлений отсутствуют, то матрица В может быть записана в следующем виде:

, где .

Запись передаточных матриц в виде (13.17) является наиболее общей. Однако в аналитическом виде сделать это можно только для простейших случаев. В основном же приходится выполнять расче­ты для конкретных числовых значений элементов матриц уравне­ния состояния и получать передаточные матрицы с числовыми зна­чениями коэффициентов, что вызывает затруднения при выполне­нии анализа и синтеза систем управления с ВМП. Вместе с этим, при определении передаточных матриц цепочных и разветвленных структур механических моделей большой размерности можно избе­жать сложных процедур вычислений по (13.17) и ограничиться толь­ко процедурами расчета собственных значений матриц, если вос­пользоваться следующей методикой.

Рассмотрим уравнение вход-выход механической системы в следующем виде:

(13.18)

В общем случае будем считать элементами вектора входных пере­менных у' обобщенные координаты и моменты упругих сил. Для оп­ределенности будем иметь в виду под обобщенными координатами уг­ловые движения элементов механической модели. Элементами векто­ра входных переменных будем считать электромагнитные моменты, причем число входных переменных считаем равным числу обобщен­ных координат. Тогда векторы у' и и' запишем в следующем виде:

; .

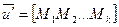Элементами передаточной матрицы размера являются передаточные функции, связывающие входные и выход­ные переменные. Первые k строк определяют связь обобщенных координат с электромагнитными моментами.

,

а следующие k-1 строк (от k+1 до 2k-1) определяют связь момен­тов упругих сил с электромагнитными моментами:

; (13.20)

.

Элементы уравнений (13.19)и(13.20) состоят из передаточных функций сепаратных каналов и перекрестных связей ММС, кото­рые могут быть определены с помощью механической модели. Для первых и строк матрицы имеем:

, (13.21)

где ; - постоянные времени, соответствующие собственным частотам колебаний полной механической модели ; - постоянные времени, соответствующие собственным частотам колебаний части механи­ческой модели, определяемые по лемме 1.

Лемма 1. В исходной модели ММС инерционные элементы с входной, выходной переменными и элементы, соединенные после­довательно между ними, считаются неподвижными. Определяются частоты свободных колебаний такой преобразованной модели. Эти частоты и соответствуют постоянным времени .

Для следующих строк матрицы от k+1 до 2k-1 имеем:

, (13.22)

где и определяются по лемме 2.

Лемма 2. В исходной модели ММС разрывается упругая связь между элементами и +1 в месте контролируемой упругой силы. Элемент с входной переменной, элемент в месте разрыва упругой свя­зи и элементы, соединенные последовательно между ними, счита­ются неподвижными. Определяются частоты свободных колебаний такой преобразованной модели. Эти частоты и соответствуют постоянным времени . Коэффициент инерции равен сумме коэффициентов инерции элементов части ММС, не связанной с неподвижными элементами, .

Принимая во внимание, что скалярный полином является общей частью для всех и , можно записать уравнение (13.18) в виде:

,

где - передаточная матрица, элементы которой определяют­ся из формул

.

Таким образом, определение матриц многосвязной механической системы сводится к использованию общего вида записи передаточных функций ее элементов и к расчету собственных частот свободных коле­баний по полной механической модели и по ее частям. Как было пока­зано выше, такой расчет сводится к расчету собственных чисел мат­риц, который также выполняется на ПК. Изложенный метод удобно применять тогда, когда число входных и выходных переменных огра­ничено, а механическая система имеет сложную структуру и описыва­ется уравнениями большой размерности.

Передаточные функции (13.21),(13.22) содержат только чисто колебательные и обратные им звенья. В действительности с учетом сил демпфирования будем иметь

(13.23)

, (13.24)

где - приведенные коэффициенты демпфирования, зави­сящие в общем случае сложным образом от параметров механи­ческой системы.

Определив передаточные матрицы механической системы, следует упростить их, исключив из рассмотрения все члены, со­ответствующие значениям частот собственных колебаний значи­тельно превышающих верхнею границу полосы пропускания се­паратных систем управления. В первую очередь это относиться к полюсам передаточных функций. Достаточно иметь два-три чле­на рассматриваемых произведений, соответствующих минималь­ным частотам колебаний для того, иметь математическое описа­ние ВМП, близкое к реальному. Что касается нулей передаточ­ных функций, то их следует ограничивать предельными значени­ями частот, но при этом следует иметь в виду, что значения мини­мальных частот колебаний, определяющих нули передаточных функций, могут быть меньшими минимальных частот колебаний, определяющих полюса, и эквивалентирование следует выполнять с определенной осторожностью.

Следует отметить, что эквивалентирование механической сис­темы можно выполнять и на уровне механической модели, если ис­пользовать методику уменьшения обобщенных координат, основан­ную на преобразовании парциальных систем ММС, содержащих или коэффициент инерции . и два коэффициента податливостей , или два коэффициента инерции , , и один коэффи­циент податливости , (коэффициент податливости определяет­ся как величина, обратная коэффициенту жесткости). Если значе­ние парциальных частот

отвечают неравенствам и , где - верхняя граница полосы пропускания сепаратной системы управления, то преобразование парциальной системы одного вида в парциальную систему другого вида не приводит к существенным искажениям ди­намической характеристики всей системы. Параметры парциальной системы одного вида преобразуются в эквивалентные параметры пар­циальной системы другого вида по формулам:

; ;

;

; ,

где штрихами обозначены преобразованные параметры.

Приведенные коэффициенты демпфирования в передаточных функциях обычно бывает сложно рассчитывать и приходится пользоваться их приближенными оценками. Но это не вносит су­щественных погрешностей в динамические модели механических систем, так как значения этих коэффициентов оказываются очень малыми и пределы их изменений для однородных сред также малы. Так, например, при деформациях металлических конструк­ций проводов коэффициенты демпфирования находятся в пределах 0,02-0,07. Поэтому, приняв средние значения этих коэффициентов, можно выполнить теоретические исследования, а далее для реаль­ных конструкций уточнить их значения по результатам эксперимен­тальных исследований.