В качестве методического примера рассмотрим построение матрицы жёсткости стержневого элемента Kj и матрицы неразрывности П, связывающей суммарные векторы обобщённых координат элементов q и узловых точек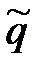 
при поперечном изгибе стержней. Расчленим стержень узловыми точками на отдельные элементы (рис. 2.5). Над стержнем показаны номера узловых сечений, а под стержнем номера элементов.
| ... |
| j |
| N 1-1 -1 |
| N 1 |
| N 1-1 -1 |
| N 1 |
| j |
| j- 1 |
| … |
Рис. 2.5
Аппроксимационную функцию прогиба внутри j -го элемента представим в виде
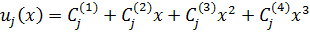
| (7.3.1) |
или в матричной форме
| (7.3.2) |
где  .
|
Компонентами вектора обобщённых координат служат поперечные перемещения 
и углы поворота 
обоих сечений элемента
 .
| (7.3.3) |
При использовании гипотезы прямой нормали угол поворота сечения равен производной от прогиба
| (7.3.4) |
| (7.3.5) |
С учётом аппроксимационных соотношений (7.3.1), (7.3.5) определим обобщённые координаты на концах j -го стержневого элемента (здесь используется локальная система координат)
| 
| (7.3.6) |
| 
|
или в матричном виде
 .
| (7.3.7) |
Отсюда следует
| (7.3.8) |
Вектор перемещений согласно равенству (7.3.2) с учётом (7.3.8) представим в форме
| (7.3.9) |
Вариацию потенциальной энергии стержневого элемента запишем в виде
| (7.3.10) |
Здесь 
– кривизна нейтральной линии изогнутого стержня
 (при малых углах изгиба)
| (7.3.11) |
L – оператор дифференцирования 
,
изгибающий момент, связанный с кривизной равенством
 .
| (7.3.12) |
Здесь 
– изгибная жёсткость.
С учётом соотношения для прогиба (7.3.9) кривизна (7.3.11) и изгибающий момент (7.3.12) следующим образом выражаются через обобщённые координаты стержневого элемента 
| (7.3.13) |
| (7.3.14) |
После подстановки соотношений (7.3.13) и (7.3.14) в (7.3.10) придем к равенству
| (7.3.15) |
Выражение для матрицы жёсткости имеет вид
| (7.3.16) |
где учтено, что от х зависит только L Ф j (величина 
в пределах элемента считается постоянной).
Так как 
, произведение 
равно следующей матрице:
 .
| (7.3.17) |
После вычисления интегралов от элементов матрицы (7.3.17) и умножения результирующей матрицы слева и справа соответственно на матрицы 
и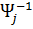 
матрица жёсткости для стержневого элемента примет вид
| (7.3.18) |
Следует отметить, что для однородного стержня матрица жёсткости может быть получена более простым путем, однако здесь проиллюстрирован общий алгоритмический подход к построению матриц жёсткости, который применим к элементам любого вида.
Теперь необходимо построить матрицу неразрывности П, связывающую суммарный вектор элементов 
с суммарным вектором узлов 
Нумерация улов и элементов показана на рис. 2.5. Матрица неразрывности П будет иметь следующий вид:
| (7.3.19) |
здесь
| (7.3.20) |
Матрица масс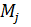 
и вектор внешних сил 
строятся на основе соотношения (7.3.9) по формулам, аналогичным (7.2.7)– (7.2.10). При этом в векторе 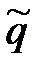необходимо в силу граничных условий защемленных краев первую и последнюю компоненты (для нулевого и N 1-го узлов) положить равными нулю
 .
|
Глобальные матрицы масс М, жёсткости K и вектор внешних сил F строятся по схеме (7.2.2.11.) – (7.2.2.13), (7.2.2.17).