В конечноэлементной трактовке задача о нагружении сводится к решению системы обыкновенных дифференциальных уравнений относительно вектора независимых обобщённых координат Х
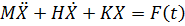
| (7.5.1) |
с начальными данными  ,
| (7.5.2) |
где 
, 
, 
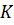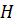– матрица масс, жёсткостей и диссипативных свойств системы, 
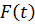– вектор внешних сил.
Среди методов определения динамических нагрузок, используемых в РКТ, наиболее широкое распространение получили метод разложения по собственным тонам колебаний и метод прямого интегрирования уравнений движения.
При использовании метода разложения по собственным тонам колебаний задача о динамическом нагружении решается в два этапа. Сначала определяются собственные частоты и формы колебаний. Затем независимо от вида модели (балка, оболочка, упругое тело) решение отыскивается в виде разложения по собственным тонам колебаний. С помощью обобщённого метода Галеркина либо вариационного принципа Лагранжа получаются обыкновенные дифференциальные уравнения для обобщённых координат.
Воспользуемся для исследования вынужденных колебаний конечно-элементного уравнения (7.5.1) методом разложения по собственным формам колебаний. Соответствующая задача о собственных колебаниях формируется из (7.5.1) путём отбрасывания диссипативных сил и правых частей уравнения. При этом решение отыскивается в виде стационарных колебаний
| (7.5.3) |
В итоге приходим к следующей задаче о собственных значениях
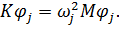
| (7.5.4) |
В результате решения этой задачи определяются собственные частоты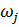 
и собственные формы колебаний 
. При этом собственные формы колебаний определяются с точностью до констант в виде множителей в силу однородности задачи (7.5.4).
|
|
Размерность вектора совпадает с размерностью вектора Х (с количеством независимых обобщённых координат задачи N 1). Максимальное количество тонов колебаний при решении этой задачи также совпадает с размерностью задачи N 1 (размерностью вектора Х).
Однако достоинством метода разложения по тонам колебаний является то, что при его использовании можно ограничиться гораздо меньшим количество тонов по сравнению с размерностью задачи. Спектр учитываемых в решении тонов колебаний должен увязываться со спектром внешних воздействий и контролироваться характером сходимости решения.
Выразим вектор кинематических параметров Х в (7.5.1) через вектор обобщённых координат T (главных координат) и матрицу собственных векторов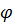 
, учитываемых в решении задачи:
| (7.5.5) |
Столбцами матрицы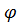 
являются l собственных векторов, учитываемых в решении задачи (7.5.1).
совокупность l векторных равенств, отвечающих различным собственным векторам и собственным частотам 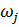(7.5.4), можно записать в виде следующего матричного равенства:
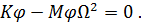
| (7.5.6) |
Матрица 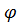имеет порядок 
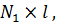где 
– порядок вектора Х, а l - количество учитываемых в решении тонов колебаний, которое может быть гораздо меньше размерности задачи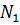 
.
Матрица 
имеет диагональную структуру
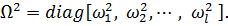
| (7.5.7) |
Подставив Х из (7.5.5) в уравнение движения (7.5.1) (предварительно опустив в нем диссипативный член) и учитывая равенство (7.5.6), будем иметь
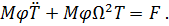
| (7.5.8) |
Умножив равенство (7.5.8) слева на матрицу 
, получим уравнение движения в обобщённых координатах
 .
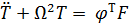| (7.5.9) |
Здесь учтена ортогональность собственных форм колебаний и их нормировка по единичной приведенной массе
|
|
| (7.5.10) |
В равенстве (7.5.10) 
– единичная матрица l -го порядка (l - количество учитываемых тонов колебаний).
Чтобы система уравнений была распадающейся, введем диссипативные силы, пропорциональные скоростям обобщённых координат. Тогда уравнение движения примет следующий окончательный вид:
| (7.5.11) |
где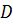 
– матрица диссипативных сил:
| (7.5.12) |
Начальные данные для интегрирования системы (7.5.11) определяются на основе заданных полей перемещений и скоростей (7.5.2) с использованием соотношения (7.5.5):
| (7.5.13) |
Умножая эти равенства слева на 
с учётом (7.5.10), придём к начальным значениям для обобщённых координат
 ,  .
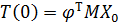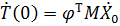| (7.5.14) |
В процессе интегрирования системы (7.5.11) c начальными данными (7.5.14) вычисляются обобщённые координаты (абсолютные перемещения и углы поворота), а затем векторы силовых факторов и напряжения в элементах.