Использование метода конечных элементов в задачах о нагружении упругих систем
Общие принципы метода конечных элементов
В последние полвека благодаря развитию вычислительной техники широкое распространение в механике сплошной среды получил метод конечных элементов (МКЭ) [12, 28]. Ниже изложены общие принципы МКЭ применительно к решению динамических задач для различных типов упругих механических систем.
Механическая система расчленяется на ряд простейших элементов с анализом их потенциальной энергии, работы внешних и инерционных сил и последующей стыковкой элементов исходя из условия неразрывности системы в узловых точках. При изгибе пластин и оболочек и в плоской теории упругости – это треугольные или четырехугольные элементы, в пространственных задачах теории упругости – тетраэдры, в стержневых системах – короткие стержни и т.д.
Метод конечных элементов существенным образом опирается на вариационные принципы механики и в значительной мере является родственным методу Ритца [26]. Аналогично методу Ритца поле перемещений внутри j -го элемента ищется в виде линейной комбинации известных базисных функций 
с неизвестными коэффициентами 
Далее будет использоваться матричная формализация, поэтому вектор перемещений внутри элемента представляется в матричной форме
| (7.1.1) |
Система базисных функций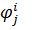 
выбирается так, чтобы существовала возможность аппроксимировать поля перемещений внутри элемента при любых значениях перемещений и углов поворота в узловых точках элемента. Этого удаётся добиться благодаря тому, что количество неизвестных констант 
и количество базисных функций задаётся равным количеству обобщённых координат элемента. При решении задач механики твёрдого деформируемого тела (оболочки, пластины, стержня) чаще всего используются перемещения и углы поворота узлов элемента.
Указанные перемещения и углы поворота узлов элемента образуют вектор обобщённых координат элемента 
.
 .
| (7.1.2) |
Подвекторы 
, входящие в (7.1.2), образованы степенями свободы узлов, входящих в j -й элемент. Число степеней свободы элемента n определяется произведением числа степеней свободы узла n 1 на число узлов элемента 
: 
.
Так, положение узла пространственного стержневого элемента (сечения стержня) характеризуется шестью степенями свободы – тремя перемещениями и тремя углами поворота (n 1 = 6). Элемент содержит два узла (n = 2), и общее число степеней свободы n = 12. При плоском напряжённом состоянии положение узловой точки характеризуется двумя перемещениями и, следовательно, треугольный элемент содержит шесть степеней свободы (n = 6).
При конечноэлементном моделировании тонкостенных элементов сложной пространственной конфигурации чаще всего используются пластиночные и стержневые элементы. Каждый узел элемента характеризуется шестью степенями свободы – тремя перемещениями и тремя углами поворота.
Очевидно, что при наличии представления (7.1.1) для поля перемещений внутри элемента легко определяются перемещения и углы поворота во всех узлах элемента с учётом координат их расположения.
Это означает, что связь между обобщёнными координатами элемента 
и константами , входящими в (7.1.1), может быть выражена в виде равенства
 .
| (7.1.3) |
Здесь 
– квадратная матрица порядка n (в силу равенства количества неизвестных констант элемента и количества обобщённых координат элемента).
С учётом равенств (7.1.3) и (7.1.1) поле перемещений внутри j -го элемента выражается через обобщённые координаты .
 .
| (7.1.4) |
Здесь N – количество элементов, на которое разбивается вся механическая система.
Следующий этап решения задачи состоит в получении вариаций потенциальной энергии, работы инерционных и внешних сил для каждого элемента и всей системы в целом в зависимости от обобщённых координат узлов на основе общего представления для полей перемещений в элементах (7.1.4). Затем из вариационного принципа Лагранжа для всей системы получаются уравнения движения относительно узловых обобщённых координат (перемещений и углов поворота).
Следующий раздел является иллюстрацией идеи метода конечных элементов на наиболее простой задаче теории упругости – плоском напряжённом состоянии.