Отдельной проблемой является определение динамических характеристик предварительно нагруженных конструкций, таких, например, как топливные баки под внутренним давлением или солнечные батареи с натянутыми поверхностями, к которым крепятся фотоэлементы.
Остановимся на построении матрицы жёсткости предварительно нагруженной конструкции. Типовой ситуацией является балочный элемент, нагруженный осевой силой.
Матрица жёсткости преднагруженной конструкции складывается из линейной матрицы, представленной в разделе 7 (…), и так называемой матрицы "дифференциальной жёсткости".
Матрица дифференциальной изгибной жёсткости балки формируется на основе дополнительной работы поперечных сил, образованных проекциями осевых сил на нормаль из-за изгиба балки (в результате линеаризации задачи).
Погонная поперечная составляющая 
от осевой силы в общем случае меняющейся по длине осевой силы 
определяется равенством (см. раздел…)
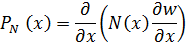
| (7.4.1) |
Здесь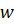 
– поперечный изгиб балки, 
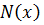– осевая сила.
В случае постоянной осевой силы 
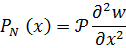
| (7.4.2) |
Для построения дополнительной матрицы жёсткости (дифференциальной жёсткости) балочного элемента для поперечного изгиба 
следует использовать ту же аппроксимацию, что и для основной матрицы, в виде кубического многочлена (см. раздел…)
| (7.4.3) |
где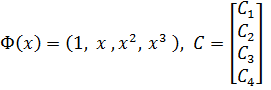 
.
Связь между обобщёнными координатами q балочного элемента и константами 
имеет вид (см. раздел ХХ)
или  ,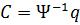
здесь  .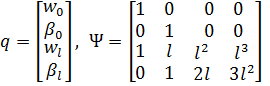
| (7.4.4) |
Компонентами обобщённого вектора 
являются перемещения 
и углы поворота 
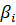в начальном и конечном сечениях элемента, 
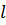– длина элемента.
С учётом (7.4.3)
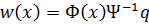
| (7.4.5) |
Дополнительная работа упругих сил выразится формулой
|
|
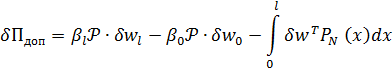
| (7.4.6) |
Здесь внеинтегральные члены определяют работу сил упругих реакций в начальном и конечном сечениях балочного элемента. Интеграл определяет работу распределённых поперечных упругих сил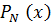 
(7.4.1), (7.4.2).
С учётом (7.4.5) выражение для поперечной силы (7.4.2) примет вид
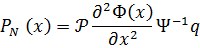
| (7.4.7) |
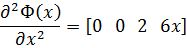
| (7.4.8) |
Внеинтегральные члены, входящие в (7.4.6), с учётом структуры вектора (7.4.4) можно записать в виде
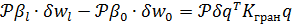
| (7.4.9) |
где
| (7.4.10) |
матрица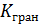 
характеризует работу упругих сил реакции на границе.
Равенство (7.4.9) легко проверяется последовательным перемножением векторов и матрицы (7.4.10).
С учётом соотношений для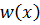 
и 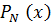(7.4.5) и (7.4.7) интеграл, входящий в (7.4.6), представится так
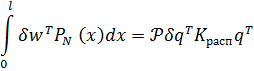
| (7.4.11) |
Здесь
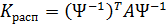
| (7.4.12) |
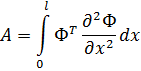
| (7.4.13) |
Подинтегральное выражение в (7.4.13) представляет собой следующую матрицу
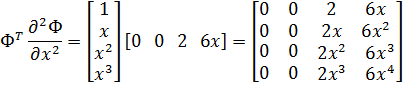
| (7.4.14) |
После интегрирования в (7.4.13) с учётом (7.4.14) матрица А примет вид
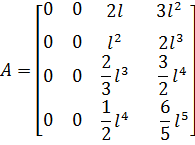
| (7.4.15) |
Подставляя выражение для интеграла и внеинтегральных членов из (7.4.11) и (7.4.9) в (7.4.6), получим соотношение для вариации дополнительной работы от поперечных составляющих, вызванных осевыми силами
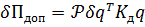
| (7.4.16) |
Здесь
 (см. (7.4.10) и (7.4.12))
| (7.4.17) |
После перемножения матриц в равенстве (7.4.12) дополнительная (или дифференциальная) матрица жёсткости (7.4.17) приобретает следующий вид
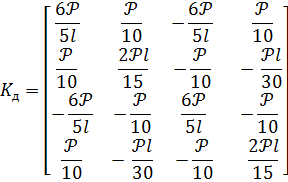
| (7.4.18) |
Для других элементов – пластин, мембран и т.п. матрица дифференциальной жёсткости формируется аналогичным образом и зависит от типа элемента, его геометрии и приложенной нагрузки.
Общая матрица жёсткости конструкции получается сложением линейной матрицы жёсткости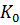 
с дифференциальной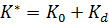 
В итоге определение собственных тонов колебаний преднагруженной конструкции сводится к решению следующей задачи:
|
|
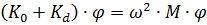
| (7.4.19) |