Для построения матриц жёсткости, масс, а также обобщённых сил в плоской динамической задаче используется вариационный принцип Лагранжа.
Вариация потенциальной энергии  равна работе инерционных сил
равна работе инерционных сил  и внешних сил
и внешних сил  (диссипативные силы будут учтены ниже)
(диссипативные силы будут учтены ниже)

| (7.2.2.1) |
Вариация потенциальной энергии


| в плоском случае | (7.2.2.2) |
С учётом равенств (7.2.1.15), (7.2.1.16)

| (7.2.2.3) |
вариация потенциальной энергии j ‑ого элемента запишется так

| (7.2.2.4) |
или
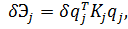
| (7.2.2.5) |
где

| (7.2.2.6) |
Работа инерционных сил с учётом (7.2.1.13):

| (7.2.2.7) |
где  – погонная масса в j -ом элементе,
– погонная масса в j -ом элементе,

| (7.2.2.8) |
где

|
Работа внешних сил с учётом (7.2.1.13)

| (7.2.2.9) |
где 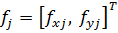 – вектор распределённых сил по j -ому элементу, в общем случае зависящих от координат и времени, или
– вектор распределённых сил по j -ому элементу, в общем случае зависящих от координат и времени, или
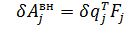 где
где  – шестимерный вектор сил – шестимерный вектор сил

| (7.2.2.10) |
Просуммировав вариации потенциальной энергии, работы инерционных и внешних сил по всем N 1 элементам, придём к следующим равенствам

| 
| (7.2.2.11) |

| 
| (7.2.2.12) |

| 
| (7.2.2.13) |
Здесь

|  – –
| 
|
| общий вектор степеней свободы всех элементов, | подвектор степеней свободы j -го элемента, | подвектор степеней свободы i ‑го узла j ‑го элемента; |
K и M – блочно-диагональные матрицы, на диагоналях которых расположены подматрицы всех элементов, F и q – блочные векторы, подвекторами которых являются шестимерные векторы всех треугольных элементов.
После подстановки (7.2.2.11)-(7.2.2.13) в вариационное соотношение (7.2.2.1) приходим к следующему равенству

| (7.2.2.14) |
Однако, в силу того, что узловые точки могут быть общими для нескольких элементов, не все вариации компонент вектора q являются независимыми. В самом деле, вспомним, что вектор q строится из векторов отдельных элементов, каждый из которых, в свою очередь, состоит из векторов узловых точек элемента. Независимыми обобщёнными координатами будут являться векторы обобщённых координат узловых точек для свободной системы. Поэтому необходимо выразить вектор обобщённых координат элементов q через независимые обобщённые координаты узловых точек  . Полный вектор обобщённых координат узловых точек запишется так:
. Полный вектор обобщённых координат узловых точек запишется так:
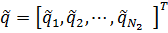
| (7.2.2.15) |
Отметим, что транспонирование векторов " Т " в данном разделе используется для их компактной записи. Размерность вектора обобщённых координат узлов q (7.2.2.15) равна 2×  , где
, где  – количество узлов.
– количество узлов.
Вектор обобщённых координат узлов  также как и вектор обобщённых координат элементов q будем задавать в глобальной системе координат (отметим, что общее количество элементов
также как и вектор обобщённых координат элементов q будем задавать в глобальной системе координат (отметим, что общее количество элементов 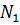 не совпадает с количеством узлов
не совпадает с количеством узлов  ).
).
Затем строится матрица П, связывающая суммарный вектор элементов q в глобальной системе с суммарным вектором узлов  .
.
 . .
| (7.2.2.16) |
По–существу, матрицей P формируются условия неразрывности системы в узловых точках, поэтому далее будем называть ее матрицей неразрывности. Матрица P зависит от конфигурации рассматриваемой области, нумерации элементов и узловых точек, а также от числа узлов, входящих в элемент.
Вектор обобщённых координат элементов q формируется из обобщённых координат узлов вектора  . Каждый i -ый узел, с которым связаны обобщённые степени свободы
. Каждый i -ый узел, с которым связаны обобщённые степени свободы  , обладает конкретными координатами
, обладает конкретными координатами  . На основе совпадения координат
. На основе совпадения координат  узловых степеней свободы
узловых степеней свободы  с координатами степеней свободы некоторых элементов
с координатами степеней свободы некоторых элементов  может формироваться матрица P.
может формироваться матрица P.
В приложении к этому разделу приводится возможный вариант построения матрицы P.
Вместе с тем переход от обобщённых координат элементов к обобщённым координатам узлов (или изначальное использование узловых обобщённых координат) является отдельной алгоритмической задачей, которая решается при разработке соответствующих программных комплексов.
Целью данного раздела является иллюстрация идеи метода конечных элементов на простейшей задаче – плоском напряжённом состоянии.
Подставив соотношения (7.2.2.16) в вариационное равенство (7.2.2.14), и учитывая в случае естественных граничных условий независимость вариаций всех компонент вектора  получим следующее конечно-элементное уравнение движения относительно узловых обобщённых координат
получим следующее конечно-элементное уравнение движения относительно узловых обобщённых координат  для свободной системы:
для свободной системы:
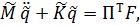
| (7.2.2.17) |
где  . .
|
Остановимся на учёте граничных условий. В случае свободной системы (отсутствие силовых факторов на границе) на компоненты вектора обобщённых координат никаких связей не налагается и уравнения движения имеют вид (7.2.2.17). Если на границе заданы кинематические условия, то есть обобщённые координаты в узлах, принадлежащих границе, являются известными или линейно-зависимыми, это означает, что на систему наложены геометрические связи. В этом случае число независимых обобщённых координат и, соответственно, независимых вариаций будет на r меньше, где r – число линейных связей, наложенных на граничные обобщённые координаты. В этом случае из вариаций потенциальной энергии, работы внешних и инерционных сил необходимо исключить r линейно зависимых обобщённых координат и получить на r уравнений типа (7.2.2.17) меньше (либо использовать метод неопределенных множителей Лагранжа).
В части учёта граничных условий итоговым результатом является следующий. В связи с тем, что в основу метода конечных элементов (МКЭ) положены вариационные принципы, граничные условия в общем случае (как связи) могут налагаться только на кинематические (геометрические) параметры – перемещения и углы поворота, а естественные (силовые) условия удовлетворяются автоматически. Этот факт является существенным достоинством МКЭ.
После учёта граничных условий, соответствующих рассматриваемой задаче, уравнение для оставшихся обобщённых координат  приобретает следующий окончательный вид
приобретает следующий окончательный вид

| (7.2.2.18) |
В уравнение (7.2.2.18) введены диссипативные силы пропорциональные вектору скорости  .
.
Для интегрирования системы уравнений задаются начальные значения вектора  :
:

| (7.2.2.19) |
Начальные значения векторов  и
и  , компонентами которых являются узловые перемещения
, компонентами которых являются узловые перемещения  и скорости
и скорости  , определяются через заданные поля перемещений и скоростей системы с учётом координат расположения узлов.
, определяются через заданные поля перемещений и скоростей системы с учётом координат расположения узлов.
Одним из характерных случаев нагружения является такой, в котором на начальном интервале времени к системе приложены статические силы, а затем силы начинают изменяться во времени. Начальное значение 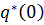 в этом случае определяется из решения статической задачи, которая получается из уравнения (7.2.2.18) путем отбрасывания инерционных и диссипативных членов
в этом случае определяется из решения статической задачи, которая получается из уравнения (7.2.2.18) путем отбрасывания инерционных и диссипативных членов
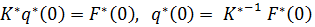
| (7.2.2.20) |
Начальные скорости обобщённых координат могут при этом быть нулевыми 
После решения системы уравнений (7.2.2.18) относительно обобщённых узловых координат  определяются обобщённые координаты элементов q с учётом (7.2.2.16) и затем определяется напряжённо-деформированное состояние в элементах конструкции с учётом соотношений (7.2.1.15) и (7.2.1.16).
определяются обобщённые координаты элементов q с учётом (7.2.2.16) и затем определяется напряжённо-деформированное состояние в элементах конструкции с учётом соотношений (7.2.1.15) и (7.2.1.16).
На этом решение задачи завершается.
Приложение к разделу 7.2.
Проиллюстрируем построение матрицы P на простом примере.
| Область W |

|

|

|

|

|

|

|

|

|
| цифра внутри элемента – его номер |
| нумерация обобщённых координат в узловых точках |

|
Нумерация узлов в элементах показана на трёх примерах (нумерация узлов в элементе осуществляется путём обхода по контуру против часовой стрелки, начиная с элементов крайнего левого узла.
|
|
|
Матрица П устанавливается по совпадению координат  . узловых степеней свободы
. узловых степеней свободы  с координатами степеней свободы элементов вектора q.
с координатами степеней свободы элементов вектора q.
Очевидно, что один и тот же узел может входить в состав нескольких элементов. Так узел  входит в состав шести элементов с номерами 1, 2, 4, 5, 7, 8. Этот факт учтен при составлении матрицы П.
входит в состав шести элементов с номерами 1, 2, 4, 5, 7, 8. Этот факт учтен при составлении матрицы П.

|
Здесь  ,
, 


|








