Критерий Романовского
Критерий Романовского применяется, если число измерений n < 20. При этом вычисляется отношение
(4.1)
где xi – проверяемое значение (наименьший/наибольший результат измерения);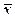 
– среднее арифметическое значение измеряемой величины; Sx – среднее квадратическое отклонение (СКО).
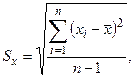(4.2)
где n – количество измерений.
В зависимости от выбранного уровня значимости, т. е. от желания экспериментатора получить уверенный результат проверки гипотезы, и числа измерений n из приложения №3 находят теоретический критерий Романовского bт, и сравнивают с ним расчетное значение b. Если b ³ bт, то результат xi считается промахом и отбрасывается.
УРОВЕНЬ ЗНАЧИМОСТИ – вероятность ошибочного отклонения (отвержения) гипотезы, в то время как она на самом деле верна. Речь идет об отклонении нулевой гипотезы.
1. 1-й уровень значимости: α ≤ 0,05.
Это 5%-ный уровень значимости. До 5% составляет вероятность того, что мы ошибочно сделали вывод о том, что различия достоверны, в то время как они недостоверны на самом деле. Можно сказать и по-другому: мы лишь на 95% уверены в том, что различия действительно достоверны.
2. 2-й уровень значимости: α ≤ 0,01.
Это 1%-ный уровень значимости. Вероятность ошибочного вывода о том, что различия достоверны, составляет не более 1%. Можно сказать и по-другому: мы на 99% уверены в том, что различия действительно достоверны.
3. 3-й уровень значимости: α ≤ 0,001.
Это 0,1%-ный уровень значимости. Всего 0,1% составляет вероятность того, что мы сделали ошибочный вывод о том, что различия достоверны. Это - самый надёжный вариант вывода о достоверности различий. Можно сказать и по-другому: мы на 99,9% уверены в том, что различия действительно достоверны.
|
|
Обычно используют уровень значимости α = 0,05, более серьезные выводы рекомендуется давать, используя уровень значимости α = 0,01 или α = 0,001.
Критерий Шарлье
Критерий Шарлье используется, если число измерений велико (n > 20). Тогда по теореме Бернулли число результатов, превышающих по абсолютного значению среднее арифметическое значение на величину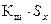 
, будет 
, где 
- значение нормированной функции Лапласа для X = Kш.
Если сомнительным в ряду результатов наблюдений является один результат, то
.
Отсюда
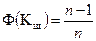. (4.3)
Значения критерия Шарлье приведены в приложении №4.
Пользуясь данным критерием, отбрасывается результат, для значения которого выполняется неравенство
. (4.4)
Критерий Диксона
Вариационный критерий Диксона удобный и достаточно мощный (с малыми вероятностями ошибок). При его применении полученные результаты наблюдений записывают в вариационный возрастающий ряд 
. Критерий Диксона определяется как
- для наибольшего значения,
- для наименьшего значения. (4.5.)
Критическая область для этого критерия 
. Значения Zq приведены в приложении №5.
Примеры 1.
При шестикратном измерении расстояний между ориентирами осей зданий получены следующие результаты:
| I | ||||||
| xi, м | 25,155 | 25,150 | 25,165 | 25,165 | 25,160 | 25,180 |
Последний результат вызывает сомнения. Произведем проверку по критерию Романовского, не является ли он промахом?
Решение:
Находим среднее арифметическое значение:
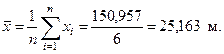
По формуле (4.2) определяем среднее квадратическое отклонение. Для удобства вычислений составим таблицу.
|
|
Оценка СКО:
Обработка результатов измерений
| № п/п | xi |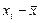 
| 
|
| 25,155 | -0,008 | 0,000064 | |
| 25,15 | -0,013 | 0,000169 | |
| 25,165 | 0,002 | 0,000004 | |
| 25,165 | 0,002 | 0,000004 | |
| 25,16 | -0,003 | 0,000009 | |
| 25,18 | 0,017 | 0,000289 | |
| 
|
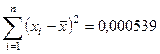
Вычисляем b для сомнительного результата измерения (при n = 6)
Ответ: критическое значение b при уровне значимости q = 0,05 для количества измерений n = 6 составляет 2,1. Поскольку 1,58 < 2,1 (b < bт), результат не является промахом и не исключается из результатов измерений.
Пример 2.
При измерении расстояний между колоннами были получены следующие результаты.
Обработка исходных данных
| № п/п | xi | 
| 
| Проверка по критерию Шарлье |
| 23,67 | 0,00 | 0,0000 | не является промахом | |
| 23,68 | 0,01 | 0,0001 | не является промахом | |
| 23,66 | -0,01 | 0,0001 | не является промахом | |
| 23,67 | 0,00 | 0,0000 | не является промахом | |
| 23,67 | 0,00 | 0,0000 | не является промахом | |
| 23,68 | 0,01 | 0,0001 | не является промахом | |
| 23,67 | 0,00 | 0,0000 | не является промахом | |
| 23,68 | 0,01 | 0,0001 | не является промахом | |
| 23,67 | 0,00 | 0,0000 | не является промахом | |
| 23,68 | 0,01 | 0,0001 | не является промахом | |
| 23,66 | -0,01 | 0,0001 | не является промахом | |
| 23,67 | 0,00 | 0,0000 | не является промахом | |
| 23,67 | 0,00 | 0,0000 | не является промахом | |
| 23,68 | 0,01 | 0,0001 | не является промахом | |
| 23,68 | 0,01 | 0,0001 | не является промахом | |
| 23,68 | 0,01 | 0,0001 | не является промахом | |
| 23,67 | 0,00 | 0,0000 | не является промахом | |
| 23,68 | 0,01 | 0,0001 | не является промахом | |
| 23,68 | 0,01 | 0,0001 | не является промахом | |
| 23,67 | 0,00 | 0,0000 | не является промахом | |
| 23,68 | 0,01 | 0,0001 | не является промахом | |
| 23,67 | 0,00 | 0,0000 | не является промахом | |
| 23,67 | 0,00 | 0,0000 | не является промахом | |
| 23,67 | 0,00 | 0,0000 | не является промахом | |
| 23,68 | 0,01 | 0,0001 | не является промахом | |
| 23,66 | -0,01 | 0,0001 | не является промахом | |
| 23,68 | 0,01 | 0,0001 | не является промахом | |
| 23,67 | 0,00 | 0,0000 | не является промахом | |
| 23,67 | 0,00 | 0,0000 | не является промахом | |
| 23,68 | 0,01 | 0,0001 | не является промахом | |
| 
| 
|
Находим СКО:
|
|
Проверяем ряд измерений на наличие промаха. Если условие 
выполняется, то результат измерения xi отбрасывается.
Критерий Шарлье для числа измерений n = 30
Kш = 2,13.
Таким образом, проверяемые значения не являются промахом и не отбрасываются из ряда измерений.
Пример 3.
Было проведено пять измерений напряжения в электросети. Получены следующие данные:
| I | |||||
| xi, В | 127,1 | 127,2 | 126,9 | 127,6 | 127,2 |
Используя критерий Диксона, проверьте на отсутствие грубых погрешностей ряд результатов измерений напряжения в электросети.
Решение:
Результат 127,6 В существенно (на первый взгляд) отличается от остальных. Необходимо проверить, не является ли он промахом.
Составим вариационный ряд из результатов измерений напряжения в электросети:
| I | |||||
| xi, В | 126,9 | 127,1 | 127,2 | 127,2 | 127,6 |
Для крайнего члена этого ряда (127,6) критерий Диксона
.
Как следует из таблицы приложения №5, по этому критерию результат 127,6 В может быть отброшен как промах лишь на уровне значимости q = 0,10.
ВАРИАНТЫ
4.1. В процессе контроля были получены следующие результаты измерительных наблюдений за одним из показателей качества:
| Вариант | ||||||||||
| № | ||||||||||
| 9,47 | 10,90 | 15,46 | 45,23 | 94,12 | 20,90 | 39,47 | 55,46 | 110,90 | 85,23 | |
| 9,49 | 11,45 | 15,42 | 45,42 | 96,12 | 21,45 | 39,49 | 55,42 | 111,45 | 85,42 | |
| 9,40 | 10,99 | 15,43 | 45,74 | 94,13 | 20,99 | 39,40 | 15,43 | 110,99 | 85,74 | |
| 9,61 | 10,96 | 14,52 | 45,42 | 95,48 | 20,96 | 39,61 | 54,52 | 110,96 | 85,42 | |
| 9,39 | 10,20 | 15,52 | 47,23 | 95,23 | 20,20 | 39,39 | 55,52 | 110,20 | 87,23 | |
| 9,41 | 9,52 | 14,14 | 47,65 | 99,12 | 19,52 | 39,41 | 54,14 | 119,52 | 87,65 | |
| 9,43 | 10,50 | 15,56 | 45,12 | 94,13 | 20,50 | 39,43 | 55,56 | 110,50 | 85,12 | |
| 9,49 | 11,00 | 14,11 | 48,23 | 94,12 | 21,00 | 39,49 | 54,11 | 111,00 | 88,23 | |
| 9,46 | 10,50 | 15,12 | 47,23 | 96,12 | 20,50 | 39,46 | 55,12 | 110,50 | 87,23 | |
| 9,42 | 11,45 | 15,12 | 46,12 | 95,48 | 21,45 | 39,42 | 55,12 | 111,45 | 86,12 |
Используя критерий Романовского выявить наличие промахов.
4.2. Используя критерий Шарлье, проверьте на отсутствие грубых погрешностей ряд результатов измерений расхода холодной воды:
| Вариант | ||||||||||
| № | ||||||||||
| 9,47 | 10,90 | 15,46 | 45,23 | 94,12 | 20,90 | 39,47 | 55,46 | 110,90 | 85,23 | |
| 9,49 | 11,45 | 15,42 | 45,42 | 96,12 | 21,45 | 39,49 | 55,42 | 111,45 | 85,42 | |
| 9,40 | 10,99 | 15,43 | 45,74 | 94,13 | 20,99 | 39,40 | 15,43 | 110,99 | 85,74 | |
| 9,61 | 10,96 | 14,52 | 45,42 | 95,48 | 20,96 | 39,61 | 54,52 | 110,96 | 85,42 | |
| 9,39 | 10,20 | 15,52 | 47,23 | 95,23 | 20,20 | 39,39 | 55,52 | 110,20 | 87,23 | |
| 9,41 | 9,52 | 14,14 | 47,65 | 99,12 | 19,52 | 39,41 | 54,14 | 119,52 | 87,65 | |
| 9,43 | 10,50 | 15,56 | 45,12 | 94,13 | 20,50 | 39,43 | 55,56 | 110,50 | 85,12 | |
| 9,49 | 11,00 | 14,11 | 48,23 | 94,12 | 21,00 | 39,49 | 54,11 | 111,00 | 88,23 | |
| 9,46 | 10,50 | 15,12 | 47,23 | 96,12 | 20,50 | 39,46 | 55,12 | 110,50 | 87,23 | |
| 9,42 | 11,45 | 15,12 | 46,12 | 95,48 | 21,45 | 39,42 | 55,12 | 111,45 | 86,12 | |
| 9,47 | 10,90 | 17,14 | 45,23 | 94,12 | 20,90 | 39,47 | 55,46 | 110,90 | 85,23 | |
| 9,49 | 11,45 | 15,46 | 45,42 | 96,12 | 21,45 | 39,49 | 55,42 | 111,45 | 85,42 | |
| 9,40 | 10,99 | 15,46 | 45,74 | 94,13 | 20,99 | 39,40 | 15,43 | 110,99 | 85,74 | |
| 9,61 | 10,96 | 15,42 | 45,42 | 95,48 | 20,96 | 39,61 | 54,52 | 110,96 | 85,42 | |
| 9,39 | 10,20 | 15,43 | 47,23 | 95,23 | 20,20 | 39,39 | 55,52 | 110,20 | 87,23 | |
| 9,41 | 9,52 | 14,52 | 47,65 | 99,12 | 19,52 | 39,41 | 54,14 | 119,52 | 87,65 | |
| 9,43 | 10,50 | 15,52 | 45,12 | 94,13 | 20,50 | 39,43 | 55,56 | 110,50 | 85,12 | |
| 9,49 | 11,00 | 14,14 | 48,23 | 94,12 | 21,00 | 39,49 | 54,11 | 111,00 | 88,23 | |
| 9,46 | 10,50 | 15,56 | 47,23 | 96,12 | 20,50 | 39,46 | 55,12 | 110,50 | 87,23 | |
| 9,42 | 11,45 | 14,11 | 46,12 | 95,48 | 21,45 | 39,42 | 55,12 | 111,45 | 86,12 | |
| 10,52 | 15,90 | 15,12 | 47,12 | 99,12 | 15,52 | 37,41 | 52,14 | 109,52 | 88,65 | |
| 12,56 | 11,45 | 15,12 | 45,23 | 94,13 | 20,50 | 39,43 | 55,56 | 110,50 | 85,12 |
4.3. Было проведено шесть измерений температуры, и получены следующие значения:
| Вариант | ||||||||||
| № | ||||||||||
| 15,4 | 5,23 | 39,47 | 55,46 | |||||||
| 15,8 | 5,42 | 39,49 | 55,42 | |||||||
| 15,4 | 5,74 | 39,40 | 15,43 | |||||||
| 14,5 | 5,42 | 39,61 | 54,52 | |||||||
| 15,5 | 7,23 | 39,39 | 55,52 | |||||||
| 14,1 | 7,65 | 39,41 | 54,14 |
Используя критерий Диксона, проверьте на отсутствие грубых погрешностей ряд результатов измерений температуры.
СПИСОК ЛИТЕРАТУРЫ
Основная литература
1. Метрология, стандартизация и сертификация [Текст]: учеб. для вузов / Авдеев, Б.Я., Алексеев, В.В., Антонюк, Е.М., [и др.]; под ред. В.В. Алексеева - М.: Академия, 2010. - 377 с. - (89143-4) и предыдущие издания
2. Метрология. Стандартизация. Сертификация [Текст]: учебник для вузов / Архипов, А.В., Зекунов, А.Г., Курилов, П.Г., [и др.]; под ред. В.М. Мишина - М.: ЮНИТИ, 2009. - 495 с. - (74075-12) и предыдущие издания
3. Метрология, стандартизация и сертификация [Текст]: учебник для вузов; [углубленный курс] / Сергеев, А.Г., Терегеря, В.В. - М.: Юрайт, 2013. - 838 с. - (95427-11) и предыдущие издания
Дополнительная литература
1. Гончаров, А.А. Мерология, стандартизация и сертификация [Текст]: учеб. пособие для вузов / Гончаров, А.А., Копылов, В.Д. - М.: Академия, 2008. - 240 с. - (73100-38)
2. Димов, Ю.В.Метрология, стандартизация и сертификация [Текст]: учебник для вузов по напр. подготовки бакалавров и магистров, и дипломир. специалистов в области техники и технологии - СПб.: Питер, 2013. - 496 с. - (100409-3) и предыдущие издания
3. Лифиц, И.М.Стандартизация, метрология и подтверждение соответствия [Текст]: учебник - М.: Юрайт, 2012. - 393 с. - (88625-2) и предыдущие издания
4. Схиртладзе, А.Г. Метрология, стандартизация и сертификация [Текст]: учеб. для вузов / Схиртладзе, А.Г., Радкевич, Я.М. - Старый Оскол: ТНТ, 2010. - 539 с. - (79512-20) и предыдущие издания.
Приложение №1
Коэффициент Стьюдента
| Число измерений, n-1 | Доверительная вероятность, P д | ||||
| 0.6 | 0.8 | 0.95. | 0.99 | 0.999 | |
| 2. | 1.376 | 3.078 | 12.706 | 63.657 | 636.61 |
| 3. | 1.061 | 1.886 | 4.303 | 9.925 | 31.598 |
| 4. | 0.978 | 1.638 | 3.182 | 5.841 | 12.941 |
| 5. | 0.941 | 1.533 | 2.776 | 4.604 | 8.610 |
| 6. | 0.920 | 1.476 | 2.571 | 4.032 | 6.859 |
| 7. | 0.906 | 1.440 | 2.447 | 3.707 | 5.959 |
| 8. | 0.896 | 1.415 | 2.365 | 3.499 | 5.405 |
| 9. | 0.889 | 1.397 | 2.306 | 3.355 | 5.041 |
| 10. | 0.883 | 1.383 | 2.262 | 3.250 | 4.781 |
| 11. | 0.879 | 1.372 | 2.228 | 3.169 | 4.587 |
| 12. | 0.876 | 1.363 | 2.201 | 3.106 | 4.437 |
| 13. | 0.873 | 1.356 | 2.179 | 3.055 | 4.318 |
| 14. | 0.870 | 1.350 | 2.160 | 3.012 | 4.221 |
| 15. | 0.868 | 1.345 | 2.145 | 2.977 | 4.140 |
| 16. | 0.866 | 1.341 | 2.131 | 2.947 | 4.073 |
| 17. | 0.865 | 1.337 | 2.120 | 2.921 | 4.015 |
| 18. | 0.863 | 1.333 | 2.110 | 2.898 | 3.965 |
| 19. | 0.862 | 1.330 | 2.101 | 2.878 | 3.922 |
| 20. | 0.861 | 1.328 | 2.093 | 2.861 | 3.883 |
| 21. | 0.860 | 1.325 | 2.086 | 2.845 | 3.850 |
| 22. | 0.859 | 1.323 | 2.080 | 2.831 | 3.819 |
| 23. | 0.858 | 1.321 | 2.074 | 2.819 | 3.792 |
| 24. | 0.858 | 1.319 | 2.069 | 2.807 | 3.767 |
| 25. | 0.857 | 1.318 | 2.064 | 2.797 | 3.745 |
| 26. | 0.856 | 1.316 | 2.060 | 2.787 | 3.725 |
| 27. | 0.856 | 1.315 | 2.056 | 2.779 | 3.707 |
| 28. | 0.855 | 1.314 | 2.052 | 2.771 | 3.690 |
| 29. | 0.855 | 1.313 | 2.048 | 2.763 | 3.674 |
| 30. | 0.854 | 1.311 | 2.045 | 2.756 | 3.659 |
| 31. | 0.854 | 1.310 | 2.042 | 2.750 | 3.646 |
| 0.851 | 1.303 | 2.021 | 2.704 | 3.551 | |
| 0.848 | 1.296 | 2.000 | 2.660 | 3.460 | |
| 0.845 | 1.289 | 1.980 | 2.617 | 3.373 | |
| ∞ | 0.842 | 1.282 | 1.960 | 2.576 | 3.291 |
Приложение №2
Приложение №3
Значения критерия Романовского bт = f (n)
| α | n = 4 | n = 6 | n = 8 | n = 10 | n = 12 | n = 15 | n = 20 |
| 0,01 | 1,73 | 2,16 | 2,43 | 2,62 | 2,75 | 2,90 | 3,08 |
| 0,02 | 1,72 | 2,13 | 2,37 | 2,54 | 2,66 | 2,80 | 2,96 |
| 0,05 | 1,71 | 2,10 | 2,27 | 2,41 | 2,52 | 2,64 | 2,78 |
| 0,10 | 1,69 | 2,00 | 2,17 | 2,29 | 2,39 | 2,49 | 2,62 |
Приложение №4
Значения критерия Шарлье
| N | |||||||
| Kш | 1,3 | 1,65 | 1,96 | 2,13 | 2,24 | 2,32 | 2,58 |
Приложение №5
Значения критерия Диксона
| N | Zq при α, равном | |||
| 0,10 | 0,05 | 0,02 | 0,01 | |
| 0,68 | 0,76 | 0,85 | 0,89 | |
| 0,56 | 0,64 | 0,78 | 0,82 | |
| 0,48 | 0,56 | 0,64 | 0,70 | |
| 0,40 | 0,47 | 0,54 | 0,59 | |
| 0,35 | 0,41 | 0,48 | 0,53 | |
| 0,29 | 0,35 | 0,41 | 0,45 | |
| 0,28 | 0,33 | 0,39 | 0,43 | |
| 0,26 | 0,31 | 0,37 | 0,41 | |
| 0,26 | 0,30 | 0,36 | 0,39 | |
| 0,22 | 0,26 | 0,31 | 0,34 |