I. Искомое значение физической величины Y и оценка погрешности при косвенных измерениях определяются на основании результатов измерений m аргументов Х1, Х2,... Хj,..., Хm, связанных с искомой величиной уравнением:
(3.1.)
Вид функции f должен быть известен из теоретических предпосылок или установлен экспериментально с погрешностью, которой можно пренебречь. Результаты измерений аргументов и оценки их погрешностей, как правило, получают путем проведения прямых измерений. По виду функциональной зависимости (3.1.) принято различать косвенные измерения с линейной и нелинейной зависимостями между измеряемой величиной и измеряемыми аргументами (или линейные и нелинейные косвенные измерения).
Обработка экспериментальных данных косвенных измерений базируется на использовании положений теории вероятностей и математической статистики о характеристиках функций случайных величин. В соответствии с этими положениями оценкой истинного значения физической величины Y, определяемой как функция случайных величин (аргументов), может служить ее значение 
, полученное после выполнения вычислительных операций со средними арифметическими значениями 
, 
,..., 
,..., 
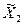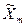аргументов в соответствии с этой функцией, т. е.
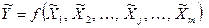, (3.2.)
При этом среднеквадратическое отклонение результата косвенного (линейного или нелинейного) измерения 
в случае, когда величины аргументы некоррелированы, т. е. не связаны между собой (наиболее важный для практики случай), определяют по формуле
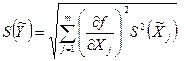(3.3)
где 
— оценка среднеквадратического отклонения результата измерения j -го аргумента; 
— частные погрешности косвенного измерения.
Частные производные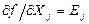 
принято называть коэффициентами влияния, а формулу (3.3.) — формулой вероятностного, или статистического, суммирования.
Относительную оценку среднеквадратического отклонения результата косвенного измерения определяют по формуле
(3.4)
Так как
(3.5)
то (3.4) можно представить в виде
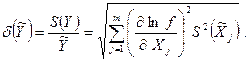(3.6)
В выражениях (3.5)-(3.6) значения частных производных 
и 
вычисляют по значениям аргументов Х1, Х2,..., Хm соответственно равным 
, 
,..., 
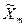, т. е. по оценкам прямых измерений. Таким образом, эти величины определяют приближенно. В некоторых частных, но важных для практики случаях коэффициенты влияния могут быть определены точно. Рассмотрим эти случаи.
1. Функция 
является линейной, т.е.
, (3.7)
где аj — постоянные коэффициенты.
Коэффициенты влияния
, (3.8)
т. е. для абсолютных погрешностей коэффициенты влияния в данном случае равны коэффициентам перед переменными в линейной функции Еj=aj. С учетом (3.8) выражение (3.3) преобразуем к виду
(3.9)
2. Функция 
– логарифмируема, т. е.
(3.10)
В этом случае удобно использовать относительные погрешности. Из (6.5.) получим
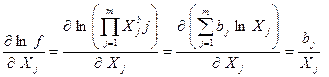(3.11)
Для частной относительной погрешности [см. выражение (3.11)] Получим
(3.12)
где 
— оценка относительного среднеквадратического отклонения результата измерения аргумента Хj.
Как видно из (3.8), коэффициенты влияния для относительных погрешностей оказываются в данном случае равными показателям степени соответствующих аргументов Wj=bj. Поэтому (3.8) можно представить в виде
. (3.13)
Если функция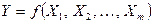 
сложная, то для определения оценки среднеквадратического отклонения результата косвенного измерения в ней выделяют отдельные зависимости — фрагменты, которые принимают за новые переменные Z1, Z2,..., Zl, и для них вычисляют оценки среднеквадратических отклонений результатов измерений. Это позволяет свести названную функцию относительно новых переменных к рассмотренным линейной или логарифмируемой функции и определить оценки среднеквадратического результата косвенного измерения.
Для определения интервальной оценки погрешности результата косвенного измерения, когда результаты наблюдений, полученные в процессе прямых измерений величин — аргументов, имеют нормальный закон распределения, используют распределение Стьюдента.
Доверительную границу случайной погрешности результата косвенного измерения вычисляют по формуле
(3.14)
В выражении (3.14) коэффициент Стьюдента определяется по таблице для принятого или заданного значения доверительной вероятности и известного эффективного числа степеней свободы kэф, которое определяется по формуле
(3.15)
где nj наблюдений, выполненное при измерении j -го аргумента.
Последовательность обработки экспериментальных данных косвенных измерений с многократными наблюдениями для некоррелированных величин:
1. Получение n результатов наблюдений Х1,Х2…Х j…Хm
2.Вычисление средних арифметических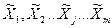 
по формуле
3. Вычисление значения 
по формуле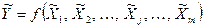 
4. Вычисление оценок среднеквадратических отклонений результатов измерений величин Х1,Х2…Х j…Хm по формуле
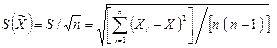
5. Вычисление оценки среднеквадратического отклонения измерения величины У по формуле
6. Вычисление числа степеней свободы Кэф по формуле Кэф =n-1
7. Принятие значений доверительной вероятности (обычно pД=0,95)
8. Определение коэффициента t в зависимости от pД и кэф по таблице распределения Стьюдента
9. Определение доверительной границы случайной погрешности 
по формуле
10. Запись результата измерения с использованием правил округления в виде:
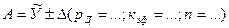
В этой последовательности записана погрешность ∆ вместо 
‚ так как предполагается что систематические погрешности полностью исключены. Число n указано, для того аргумента, при измерении которого выполнено наименьшее число наблюдений. Для случая, когда значениями неисключенных систематических погрешностей нельзя пренебречь, разработана методика оценки суммарной погрешности, близкая к ранее приведенной для прямого измерения с многократным наблюдениями.
При определении погрешности косвенного измерения важными являются установление частных погрешностей, которые в основном определяют погрешность косвенного измерения, и исключения из рассмотрения тех погрешностей которые не оказывают на общую погрешность почти никакого влияния. Определение последних связано с процедурой округления результата измерения и оценки погрешности.
Если в выражении (6.13) какая либо частная погрешность такова, что выполняется условие
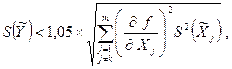(3.16)
то этой частной погрешностью можно пренебречь, так как при округлении уже число 1,0499 принимается за 1,0.
Из выражения (3.16) можно получить формулу для вычисления k -й частной погрешности:
. (3.17)
Это выражение называют критерием ничтожности погрешности. Погрешности, отвечающие этому критерию, называют ничтожными или ничтожно малыми, поэтому их не принимают во внимание при вычислении общей оценки погрешности косвенного измерения.
Последовательность обработки экспериментальных данных косвенных измерений с многократными наблюдениями:
II. Оценка результата косвенного однократного измерения определяется на основе оценок аргументов, определяемых путем прямых измерений с однократными наблюдениями:
. (3.18)
Результат косвенного измерения записывают в виде
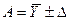, (3.19)
где D — оценка погрешности косвенного измерения.
. (3.20)
Относительную погрешность косвенных измерений вычисляют по формуле:
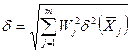. (3.21)
Предварительно определив относительные погрешности 
.
Пример 1.
Определите мощность в цепи, если
| I,мА | 0,36 | 0,32 | 0,32 | 0,30 | 0,31 | 0,32 | 0,33 | 0,35 | 0,36 | 0,32 |
| U, мВ | 10,8 | 10,5 | 9,25 | 9,60 | 10,1 | 10,0 | 9,55 | 10,3 | 9,70 | 10,2 |
Доверительная вероятность 0,95.
| Дано: I1=0.3 мА U1=10.5 мВ I2=0.3 мА U2=10.5 мВ I3=0.4 мА U3=9.5 мВ I4=0.3 мА U4=9.5 мВ I5=0.4 мА U5=10.10 мВ I6=0.4 мА U6=10.00 мВ I7=0.5 мА U7=9.55 мВ I8=0.5 мА U8=10.00 мВ I9=0.4 мА U9=9.50 мВ I10=0.4 мА U10=10.00 мВ РД=0,95 | Решение:
См. последовательность действий стр.15
1.Вычисление средних арифметических
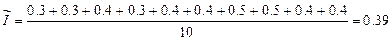
2. Вычисление W=U∙I
W=0.39∙9.9=3.86 мВт
3. Вычисление оценок СКО результатов измерений величин
|
| Найти: W± Δ |
4. Вычисление оценки среднеквадратического отклонения измерения величины 
5. Вычисление числа степеней свободы Кэф по формуле Кэф =n-1
Кэф=10-1=9
6. Принятие значений доверительной вероятности pД=0,95
7. Определение коэффициента t в зависимости от pД и кэф по таблице распределения Стьюдента
t=2.306
8. Определение доверительной границы случайной погрешности 
по формуле
10. Запись результата измерения с использованием правил округления в виде:
мВт (рд=0,95; kэф=9; n=10)
Ответ: мВт (рд=0,95; kэф=9; n=10)
Пример 2.
Определить значение потребленной мощности в цепи, оценить погрешность ее измерения и записать результат, если ток в цепи равен (0,39 ± 0,02) мА; напряжение составляет (9,9 ± 0,12) мВ. Границы погрешности указаны для вероятности 0,95 при нормальных условиях измерения.
| Дано: I=(0,39 ± 0,02) мА U=(9,9 ± 0,12) мВ РД=0,95 | Решение:
1.Вычисление потребленной мощности в цепи:
Вычисление W=U∙I
W=0.39∙9.9=3.86 мВт
2. Вычисление абсолютной погрешности
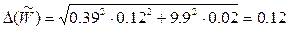Отве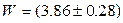т:  мВт
|
| Найти: W± Δw |
ВАРИАНТ