Метод конечных элементов

Метод конечных элементов(МКЭ) — численный метод решения задач прикладной механики.

Широко используется для решения задач механики деформируемого твёрдого тела, теплоообмена, гидродинамики и электромагнитных полей. С точки зрения вычислительной математики, идея метода конечных элементов заключается в том, что минимизация функционала вариационной задачи осуществляется на совокупности функций, каждая из которых определена на своей подобласти, для численного анализа системы позволяет рассматривать его как одну из конкретных ветвей диакоптики — общего метода исследования систем путём их расчленения. Возникновение метода конечных элементов связано с решением задач космических исследований в 1950-х годах (идея МКЭ была разработана советскими учёными ещё в 1936 году, но из-за неразвитости вычислительной техники метод не получил развитие). Этот метод возник из строительной механики и теории упругости, а уже затем было получено его математическое обоснование. Существенный толчок в своём развитии МКЭ получил в 1963 году после того, как было доказано то, что его можно рассматривать, как один из вариантов распространённого в строительной механике метода Рэлея-Ритца, который путём минимизации потенциальной энергии сводит задачу к системе дифференциальных уравнений или систем линейных уравнений равновесия. После того, как была установлена связь МКЭ с процедурой минимизации, он стал применяться к задачам описываемым уравнениями Лапласа или Пуассона. Область применения МКЭ значительно расширилась, когда было установлено (в 1968 году), что уравнения, определяющие элементы в задачах могут быть легко получены с помощью вариантов метода взвешенных невязок, таких как метод Галёркина, или метод наименьших квадратов. Это сыграло важную роль в теоретическом обосновании МКЭ, так как позволило применять его при решении многих типов дифференциальных уравнений. Таким образом, метод конечных элементов превратился в общий метод численного решения.

С развитием вычислительных средств возможности метода постоянно расширяются, также расширяется и класс решаемых задач. Практически все современные расчёты на прочность проводят, используя метод конечных элементов.

Метод конечных элементов (МКЭ) является сеточным методом, предназначенным для решения задач микроуровня, для которого модель объекта задается системой дифференциальных уравнений в частных производных с заданными краевыми условиями.

Метод конечных элементов (МКЭ) является сеточным методом, предназначенным для решения задач микроуровня, для которого модель объекта задается системой дифференциальных уравнений в частных производных с заданными краевыми условиями.

LV + P =0

V(Г) = Vг

Здесь L - дифференциальный оператор (например оператор Лапласа), V - фазовая переменная - неизвестная функция, которую следует найти, P -величина, независящая от V. V(Г)=Vг – граничное условие первого рода (Дирихле), то есть на границе задано значение фазовой переменной.

Будем искать решение с помощью функции, имеющей следующий вид:

Здесь V* - приближенное решение, F - функция, удовлетворяющая граничным условиям, Nm - пробные функции, которые на границе области должны быть равны нулю, Am – неизвестные коэффициенты, которые необходимо отыскать из условия наилучшего удовлетворения дифференциальному оператору, M- количество пробных функций. Если подставить V* висходный дифференциальный оператор, то получим невязку, принимающую в различных точках области разное значение.

R=LV*+P

Необходимо сформулировать условие, позволяющее минимизировать эту невязку по всей области. Одним из вариантов такого условия может быть следующее уравнение:

Здесь Wn - некоторые весовые функции, в зависимости от выбора которых различают варианты метода взвешенных невязок, S- область пространства, в которой ищется решение. При выборе в качестве весовых функций дельта - функций будем иметь метод, который получил название метод поточечной коллокации, для кусочно-постоянных функций - метод коллокации по подобластям, но наиболее распространенным является метод Галеркина, в котором в качестве весовых функций выбираются пробные функции N. В этом случае, если количество пробных функций равно количеству весовых функций, после раскрытия определенных интегралов приходим к замкнутой системе алгебраических уравнений относительно коэффициентов A.

KA + Q = 0

где коэффициенты матрицы K и вектора Q вычисляются по формулам:

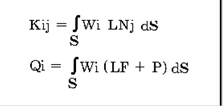
После нахождения коэффициентов A и подстановки их в (1), получаем решение исходной задачи. Недостатки метода взвешенных невязок очевидны: поскольку решение ищется сразу по всей области, то количество пробных и весовых функций должно быть значительным для обеспечения приемлемой точности, но при этом возникают трудности при вычислении коэффициентов Kij и Qi, особенно при решении плоских и объемных задач, когда потребуется вычисление двойных и тройных интегралов по областям с криволинейными границами. Поэтому на практике этот метод не использовался, пока не был изобретен метод конечных элементов (МКЭ). Идея метода заключается в следующем: в методе взвешенных невязок воспользоваться простыми пробными и весовыми функциями, но не во всей области S, а ее отдельных подобластях (конечных элементах), а точность решения задачи обеспечить использованием большого числа конечных элементов (КЭ), при этом КЭ могут быть простой формы и вычисление интегралов по ним не должно вызывать особых затруднений. Математически переход от метода взвешенных невязок к МКЭ осуществляется с использованием специальных пробных функций, которые также называются глобальными базисными функциями, обладающих следующими свойствами:

1) в узле аппроксимации функции имеют значение равное единице;

2) отличны от нуля только в КЭ, содержащих этот узел аппроксимации, во всей остальной области равны нулю.

Задачу (1.2.11)-(1.2.20) решаем в переменных скорость-давление в слабой формулировке.

После подстановки компонентов девиатора тензора напряжений (1.1.8)-(1.1.9), выраженных через производные от функции скорости в уравнения (1.1.5)-(1.1.7) имеем

, (4.1)

. (4.2)

В качестве базисных функций для определения значений полей скорости и давления используем функции формы для четырехугольного div-устойчивого конечного элемента первого порядка.

В результате проецирования уравнений (4.1)-(4.2), в смысле Галеркина на базисные функции и соответственно, система проекционно-сеточных уравнений для конечного элемента будет иметь вид:

, (4.3)

, (4.4)

где , , , - объем -го конечного элемента.

Используя теорему Остроградского-Гаусса, понизим порядок производных в (4.10). В результате получим

(4.5)

где - вектор нормали к границе, - границы -го конечного элемента.

В результате модификации реологической модели (1.1)-(1.2) путем введения малого параметра выражение для определения полного тензора напряжений будет иметь вид

, . (4.6)

Выражение для определения неньютоновской вязкости (1.2) трансформируется в

, (4.7)

, (4.8)

Очевидно, что . При решении задачи (1.2.11)-(1.2.20) методом конечных элементов с учетом (4.6)-(4.7) параметр (коэффициент регуляризации) выбирается путем численного эксперимента как наименьшее значение, приводящее к устойчивому процессу численного решения с обеспечением требуемой точности численных расчетов

, (4.9)

где - константа, зависящая от и .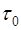

В данной работе значение принималось равным .

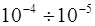C учетом регуляризации реологической модели (4.7)-(4.8) система проекционно-сеточных уравнений для задачи (1.2.11)-(1.2.20) будет иметь вид:

, (4.10)

(4.11)

(4.12)

Для удобства описания алгоритма решения задачи систему уравнений (4.10)-(4.12) представим в матричном виде

, (4.13)

где элементы матриц определяются следующими интегралами (в локальной системе координат):

, (4.14)

, (4.15)

, (4.16)

, (4.17)

, (4.18)

, (4.19)

. (4.20)

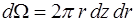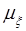Здесь (); ; - объем конечного элемента; - текущий радиус (здесь и далее в работе индекс в выражениях для и 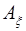опущен).

Связь между производными от базисных функций по глобальным (, ) и локальным (, ) координатам будем производить с использованием следующей матрицы соответствия:

, т. е. (4.21)

, (4.22)

где и , (4.23)

соответственно матрица Якоби и обратная к ней, - определитель матрицы Якоби , , , . (4.24)

С учетом преобразований (4.21)-(4.24) компоненты матрицы жесткости (4.13) для изопараметрического div-устойчивого конечного элемента будут определяться как

, (4.25)

, (4.26)

, (4.27)

, (4.28)

, (4.29)

, (4.30)

. (4.31)

Подинтегральные функции в (4.25)-(4.30) являются сложными полиномиальными функциями локальных координат. Поэтому для их вычисления необходимо использовать специальные методы численного интегрирования. В данной работе будем использовать метод квадратур Гаусса, как один из наиболее распространенных и эффективных методов численного интегрирования. Представим полученные в процессе дискретизации двойные интегралы в виде

. (4.32)

Тогда применение к (4.32) квадратурной формулы Гаусса приводит к

, (4.33)

где , - точки интегрирования по каждой координате, , - весовые коэффициенты, - порядок интегрирования.