Физическая постановка задачи

Курсовой проект

«Математическое моделирование движения нелинейно-вязкопластичной жидкости в осесимметричном канале с внезапным сужением»

 

 

Выполнил: Николаев Д.С.

Проверил: Чехонин К.А.

 

Хабаровск

Оглавление

 

Оглавление. 2

Перечень условных обозначений. 3

Введение. 5

1. Физическая постановка задачи. 7

2. Математическая постановка задачи. 9

3. Методы решения. 13

3.1. Метод конечных разностей. 13

3.2. Метод контрольного объема. 15

3.3. Метод конечных элементов. 28

4. Проектирование течения жидкости в канале переменного сечения прикладными программными продуктами. 36

4.1 Основные соотношения. 36

4.2 Постановка задачи. 37

4.3 Моделирование задачи. 37

Список литературы.. 45

 

Перечень условных обозначений

В список включены наиболее употребительные условные обозначения и сокращения. Вновь встречающиеся обозначения оговариваются отдельно.

- пространственные координаты;

- координаты в декартовой системе;

- цилиндрические координаты;

- объем тела;

- расчетная область;

- поверхность, ограничивающая область;

- характерный размер области;

- характерная скорость;

- гидродинамическое давление;

- плотность жидкости;

- коэффициент релаксации;

- переменная времени;

- пластическая вязкость среды;

- эффективная неньютоновская вязкость;

- предел текучести;

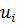- компоненты вектора скорости;

- компоненты тензора напряжений;

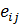- компоненты тензора скоростей деформаций;

- метрический тензор;

Нумерация формул и рисунков сквозная в пределах всего текста.

Введение

Исследование peoдинамических процессов при течении нелинейно-вязкопластичных жидкостей имеет большое прикладное значение для ряда отраслей машиностроения, добывающей, пищевой, перерабатывающей, химической промьшленности, энергетики и т.д. Математическое моделирование процессов течения неньютоновских сред с использованием современных средств вычислительной техники позволяет заменить громоздкий и дорогостоящий натурный эксперимент и с достаточно высокой точностью определить структуру течения и реологические свойства.

При моделировании peoдинамических процессов в нелинейно-вязкопластичных жидкостях является важным выбор вида уравнения, описывающего зависимость скорости деформации сдвига в каждой точке среды от напряжения сдвига в данной точке (реологическое уравнение состояния).

Основной сложностью численного моделирования движения нелинейно-вязкопластичной жидкости является наличие у среды предельного напряжения сдвига (предела текучести). В этом случае математическая постановка задачи даже для простейших типов течений приводит к краевым задачам для нелинейных уравнений в областях с «неизвестными границами»

Таким образом, сложности численного моделирования движения нелинейно-вязкопластичных сред обусловлены:

нелинейностью свойств жидкости в функции от скорости деформаций и наличием у неё предела текучести;

- наличием неизвестной свободной границы «вязкопластичная жидкость - жесткое ядро», приводящей к краевым задачам на вариационные неравенства;

- наличием сингулярности в области квазитвердого ядра, в случае использования модели эффективной вязкости {/и ^ со при ву-^О), где /л – эффективная вязкость, - тензор скорости деформаций);

- сложностью решения нелинейных плохо обусловленных систем проекционно-сеточных уравнений.

Среди всего многообразия краевых задач о течении нелинейно-вязкопластичной жидкости особое место занимает задача о её движении в области с внезапным сужением двух цилиндров. Данный тип течения имеет важное практическое значение и реализуется в технологиях переработки полимеров, реометрических приборах и т.д. Данная задача может рассматриваться как тестовая (вытекание жидкости из бесконечного резервуара). В области внезапного сужения канала поток жидкости подвергается значительной пространственной перестройке, формируется угловой вихрь вторичного течения. Важным в этой задаче является определение зависимости геометрических парметров подобласти углового вихря, его интенсивности, длины области перестройки течения и потерь давления от реологических параметров среды.

Физическая постановка задачи

Рассмотрим медленное ползущее течение высоковязкой нелинейно-вязкопластичной жидкости, описываемой реологической моделью Шульмана. Рассматриваемая среда является изотропной, плотность жидкости принимаем постоянной. Течение происходит в изотермических условиях при отсутствии массовых сил.

Жидкость течет с постоянным расходом в области внезапного сужения двух каналов цилиндрической формы с соотношением их диаметров 4:1. При ламинарном течении в трубе определенного диаметра с последующим сужением канала поток установившегося течения жидкости подвергается значительной пространственной перестройке в окрестности зоны сужения. Характер такой перестройки потока позволяет определять реологические параметры исследуемой жидкости и выявлять физические закономерности.

Характерной гидродинамической особенностью данного типа течения является наличие у среды предела текучести и, как следствие, области квазитвердого течения с неизвестными пространственными границами.

С учетом принятого предположения о связи тензора напряжений и скоростей деформаций в качестве реологического уравнения используем феноменологическую четырехпараметрическую модель Шульмана, которую представим в виде

(1.1)

, (1.2)

где - эффективная вязкость, - предел текучести, - пластическая вязкость, - параметры нелиней–ности реологической модели, - тензор скоростей деформаций, определяемый как

, (1.3)

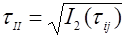- интенсивность касательных напряжений,

- интенсивность скоростей деформаций,

- вторые инварианты тензоров напряжений и скоростей деформаций соответственно, .