Основные соотношения
При решении различных научных и в особенности технических задач, связанных с течением жидкостей по трубам, одним из важных является вопрос о величине гидравлических потерь.
Обычно трубопроводы представляют собой систему, состоящую собственно из трубы или «русла» и различных конструктивных включений (заслонки, резкие сужения, расширения, и пр.). Под термином гидравлические потери принято понимать величину потерь энергии (напора), затрачиваемой на преодоление сопротивления движению жидкости, которая включает по отдельности:
потери напора на преодоление гидравлических сопротивлений по длине пропорциональны длине участков трубы или русла, по которым движется жидкость (так называемые потери по длине);
потери напора на преодоление гидравлических сопротивлений на участках трубы, находящихся в непосредственной близости к местным конструктивным устройствам (так называемые местные потери).
Обычно полагают, что общие потери напора в системе труб равны сумме потерь напора по длине отдельных участков и всех местных потерь. Потери энергии напора в основном обусловлены необратимым переходом механической энергии потока в тепловую. Механизмы действия сил сопротивления в конкретных системах трубопроводов очень сложны и практически не поддаются аналитическому описанию. Поэтому при расчетах потерь напора используют, как правило, эмпирические соотношения.
Ниже в качестве учебных задач, иллюстрирующих проблему оценки гидравлических потерь, рассматриваются задачи оценки местных потерь на примере потери давления при внезапном изменении сечения круглой трубы.
Следует отметить, что при резком переходе от одного диаметра трубы к другому или при обтекании потоком какой-либо резкой преграды, может происходить отрыв струи от стенок канала. При этом возникают области вихревого течения; остальную часть потока называют транзитной (спутной) струей (рис. 4.1.1).
Постановка задачи
В задаче проводится количественная оценка потерь полного давления при расширении потока Δ Р а также влияния геометрии изменения сечения канала на величину потерь. Кроме этого, визуально изучается явление отрыва течения при расширении потока несжимаемой жидкости.
Условие задачи
Несжимаемая турбулентная жидкость течет по каналу переменного сечения заданной формы. При резком сужении канала возможно образование вихрей (водоворотных областей) и отрыв потока, что существенно влияет на величину гидравлических потерь. Задача состоит в том, чтобы рассчитать сужение потока, задав втекание жидкости со стороны широкой части трубы.
Моделирование задачи
Для моделирования задачи был использован пакет COMSOL Multiphysics, позволяющий решать широкий спектр задач моделирования с использованием метода конечных элементов, как в зависимости от времени, так и для получения статической картинки.
Первым делом необходимо ввести константы, указанные в задании.

Рис. 4.3.1. Добавление переменных
После того как переменные добавлены, можно переходить к созданию геометрии, в которой будет происходить моделирование. Геометрия будет создана путем создания двух прямоугольников и взятии операции разницы между ними. В данном моделировании использовались следующие параметры:
Длина области без сужения L1= 1м.
Длина области с сужением L2= 1м.
Радиус области без сужения R1= 0,11 м.
Радиус области с сужением R2= 0.0275 м.

Рис. 4.3.2. Создание геометрии
После того как область создана, необходимо выбрать материал, который будет использоваться в моделировании. В данном случае будем использовать газолин, т.к. он обладает необходимыми нам физическими свойствами (при использовании, например, воды, которая не является нелинейно-вязкой жидкостью, моделирование не будет произведено в связи с ошибкой в вычислениях).

Рис. 4.3.3. Выбор материала
После выбора материала необходимо задать параметры потока и граничные условия, согласно которым будет решена задача.

Рис. 4.3.4. Настройка параметров потока
Как видно из рисунка 4.3.4, мы указываем то, что жидкость несжимаема и подчиняется уравнению Стокса. Можно посмотреть уравнения, чтобы убедиться, что они соответствуют нашим уравнениям, описанным в постановке задачи.
Главное, что необходимо установить – зависимость скорости течения жидкости по x на границе Г1. По умолчанию, большинство границ является твердыми, т.е. скорость жидкости на границе равна нулю – что и надо нам по условию задачи.

Рис. 4.3.5. Установка граничных условий
Следующим шагом будет генерация сетки элементов.

Рис. 4.3.6. Настройка генерации сетки элементов (mesh).
Согласно условию задачи, сетка должна состоять из треугольных элементов, поэтому добавляем элемент Free Triangular, который будет занимать всю область моделирования, а затем настраиваем размеры одного треугольников. Сетка адаптивная, что означает динамичность размеров треугольников в местах с повышенной скоростью изменения величин. Приведенные на рисунке настройки дадут нам сетку следующего вида:

Рис. 4.3.7. Сетка элементов
После генерации можно переходить непосредственно к расчетам. Проведя моделирование на основной схеме эксперимента, получим следующую картину давления.
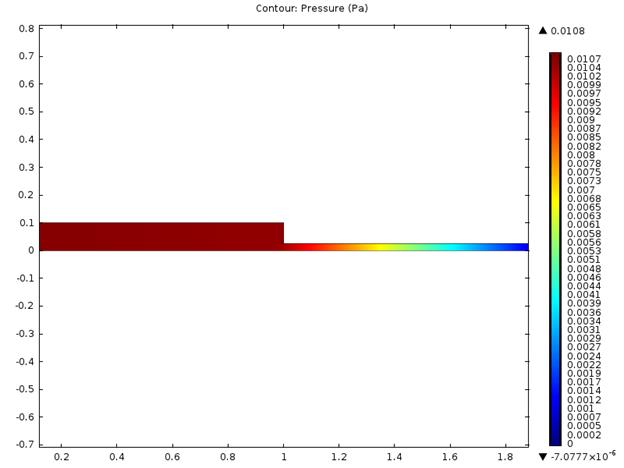
Рис. 4.3.8. График давления для рассчитанной области.

Рис. 4.3.9. График скоростей для рассчитанной области.
Как видно из графика, давление, достигающее своего максимума у границы Г1 остается практически постоянным на протяжении всего и широкого участка рассматриваемого канала, и постепенно падает при вхождении в узкую часть канала, что соответствует рассматриваемой физической задаче.
В задаче о течении нелинейно-вязкопластичной жидкости в области с внезапным сужением при постоянном расходе  является важным описание структуры потока с определением точного перепада давления
является важным описание структуры потока с определением точного перепада давления  и его входных потерь, обусловленных перестройкой течения в области внезапного сужения канала.
и его входных потерь, обусловленных перестройкой течения в области внезапного сужения канала.
 , (4.1)
, (4.1)
где  - перепад давления во всей области
- перепад давления во всей области  ;
; 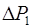 - перепад давления в области с радиусом
- перепад давления в области с радиусом  и длиной
и длиной  ;
;  - перепад давления в области с радиусом
- перепад давления в области с радиусом  и длиной
и длиной  (рис. 1.2.1.);
(рис. 1.2.1.);  - значение напряжения трения на стенке трубы меньшего диаметра на выходе области.
- значение напряжения трения на стенке трубы меньшего диаметра на выходе области.
В (4.1) величину  называют поправкой Куэтта для давления.
называют поправкой Куэтта для давления.
Значение  при известном
при известном  и заданных геометрических параметрах области после сужения канала можно определить как
и заданных геометрических параметрах области после сужения канала можно определить как
 , (4.2)
, (4.2)
где  - радиус,
- радиус, 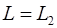 - длина участка трубы после сужения канала.
- длина участка трубы после сужения канала.
Подставляя (5.2) в (5.1), получим
 (4.3)
(4.3)
Подставив значения в (4.3) мы получим поправку Куэтта 
Экспериментальное значение поправки Куэтта для ньютоновской жидкости  , это доказывает что жидкость используемая в моделировании является не ньютоновской.
, это доказывает что жидкость используемая в моделировании является не ньютоновской.
Список литературы
1. Прандтль Л. Гидроаэромеханика. - Ижевск, РХД, 2000
2. Ламб Г. Гидродинамика. - М., ГИТТЛ, 1947
3. Жуковский Н.Е. Собрание сочинений. Том. 2. Гидродинамика. - М., ГИТТЛ, 1949
4. Лойцянский Л.Г. Механика жидкости и газа. - М., Дрофа, 2003
5. Лойцянский Л.Г. Ламинарный пограничный слой. - М., ГИФМЛ, 1962
6. Кочин Н.Е., Кибель И.А., Розе Н.В. Теор. гидромеханика. В 2-х ч. - М., Физматлит, 1963
7. Ландау Л.Д., Лифшиц Е.М. Теор. физика в 10 т. Том 6. Гидродинамика. - М., Наука, 1986
8. Шлихтинг Г. Теория пограничного слоя. - М., Наука, 1974