С учетом принятых допущений в основу математического описания процесса течения нелинейно-вязкопластичной жидкости положим уравнения механики сплошной среды, включающие в себя:
- уравнение движения
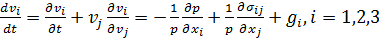(1.3)
где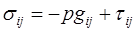 
- тензор напряжений, 
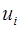- компоненты вектора скорости, 
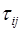- девиатор тензора вязких напряжений, 
- гидродинамическое давление,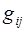 
- метрический тензор.
- уравнение неразрывности
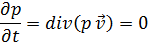
Так как жидкость несжимаема, ее плотность постоянна 
следовательно 
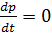и p можно вынести из оператора диверценции и сократить.
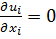(1.4)
Для осесимметричного случая в правой цилиндрической системе координат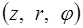 
, систему уравнений (1.3)-(1.4) представим как
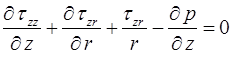, (1.5)
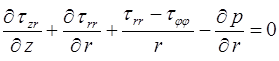, (1.6)
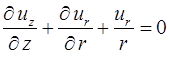. (1.7)
где компоненты девиатора тензора напряжений имеют вид:
, 
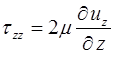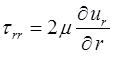, (1.8)
, 
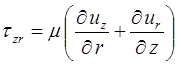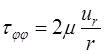. (1.9)
Выражение для интенсивности скоростей деформаций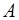 
в цилиндрической системе координат будем определять как
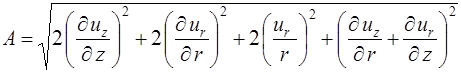(1.10)
Подставляя (1.8)-(1.9) в (1.5)-(1.6), получим
(1.11)
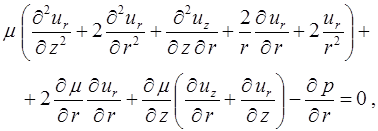(1.12)
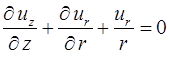. (1.13)
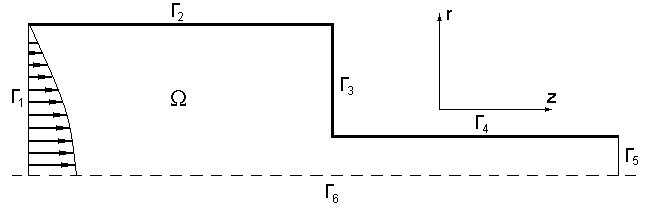
Рис. 1. Границы расчетной области
Уравнения (1.11)-(1.13) замыкаем следующими граничными условиями. Для этого границу расчетной области (рис. 1) представим в ви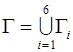де 
, где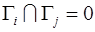 
, 
.
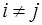С учетом введенных обозначений для рассматриваемой области 
(рис. 2) граничные условия имеют вид:
- на входе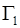 
в область течения задаем профиль установившегося течения жидкости Шульмана с заданными значениями реологических параметров и известным постоянным расходом (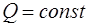
):
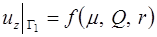, (1.14)
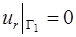; (1.15)
- на твердых стенках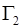 
, 
, 
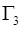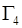- условия непротекания и прилипания
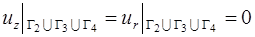; (1.16)
- на выходе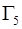 
из расчетной области задаем слабые условия установления течения
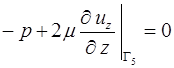, (1.17)
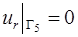; (1.18)
- на оси симметрии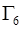 
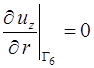, (1.19)
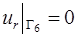. (1.20)
Таким образом, задача о течении высоковязкой нелинейно-вязкопластичной жидкости в осесимметричном канале с внезапным сужением сводится к определению компонентов вектора скорости (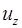
, 
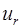), эффективной вязкости 
и давления , удовлетворяющих уравнениям (1.11)-(1.13) и граничным условиям (1.14)-(1.20).
|
|
Значения параметров задачи принимают вид:
,
,
,
,
,
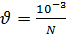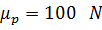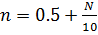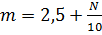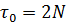H=1,
,
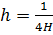R1=N,
R2=N/4,
N=11.
Методы решения
Метод конечных разностей
Обычная процедура получения конечно-разностных уравнений заключается в аппроксимации производных в дифференциальном уравнении обрезанными рядами Тэйлора. Рассмотрим узловые точки, показанные на рис. 2.
Разложение в ряд Тэйлора около узловой точки 2, расположенной посередине междуточками 1 и 3 (так что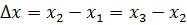 
), дает
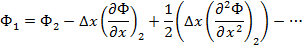
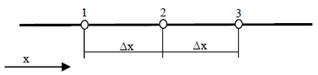
Рис. 2. Три последовательные узловые точки, используемые при разложении в ряд Тэйлора
Отбрасывая члены обоих рядов, начиная с четвертого, вычитая и складывая уравнения, получаем
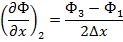
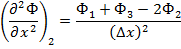
Подставляя эти выражения в дифференциальные уравнения, можно получить конечно-разностные уравнения.
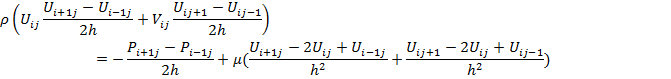
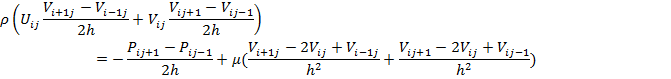
Из полученных уравнений находим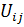 
, 
, 
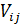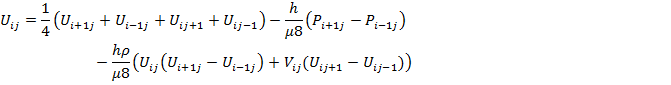
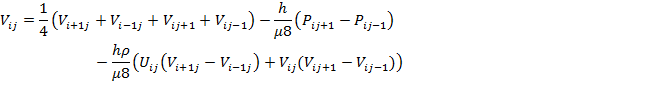
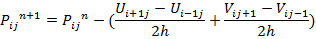
В данном методе предполагается, что изменение Ф в зависимости от х близко к полиномиальному, так что высшими производными можно пренебречь. Однако это предположение приводит к нежелательным последствиям, например, для случая экспоненциального изменения Ф.
Вывод с помощью рядов Тэйлора сравнительно прост, но менее гибок и не способствует пониманию физического смысла членов уравнения.