Способы детерминированного факторного анализа

Детерминированный факторный анализ (функциональный) представляет собой методику исследования влияния факторов, связь которых с результативным показателем носит функциональный характер, т.е. результативный показатель может быть представлен в виде произведения, частного или алгебраической суммы факторов.

Последовательность детерминированного факторного анализа

1. Отбор факторов, которые определяют исследуемый результативный показатель.

2. Классификация и систематизация факторов (факторы первого порядка, второго и т.д.).

3. Определение формы зависимости между факторами и результативными показателями.

4. Моделирование взаимосвязей между результативными и факторными показателями.

5. Расчет влияния факторов и оценка роли каждого из них на изменение результативного показателя.

2.1 Способ цепной подстановки. Используется для расчета влияния факторов во всех типах детерминированных факторных моделей: аддитивных, мультипликативных, кратных и смешанных.

Сущность приема цепных подстановок заключается в последовательной замене базисной величины частного показателя фактической величиной этого показателя и измерение влияния произведенной замены на изменение величины изучаемого результативного показателя.

Число подстановок равно числу входящих в расчетную формулу частных показателей, а число последовательных расчетов на единицу больше, так как для определения общей величины изменения результативного показателя приводится базисный расчет, в котором все показатели отражаются в базисных величинах. При решении задач способом цепных подстановок и производными от него способами используется прием элиминирования. С помощью данного приема при оценке влияния каждого фактора на результативный показатель предполагается, что остальные факторы на изменения результативного показателя влияния не оказывают.

Последовательность применения метода цепных подстановок представлена

в табл.1.1.

Исходная модель – мультипликативная

Таблица 1.1.

Порядковый номер	Взаимодействие частных показателей	Результативный показатель Y	Изменение результативного показателя
Расчета	Подста новки	a	b	c	d	Под воздействием частного показателя	Расчет изменения
	-						-	-
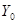
							a
							b
							c
							d
Балансовая увязка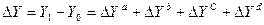

Главное требование при применении приема цепных подстановок заключается в правильности выбора очередности частных факторов при написании формулы результативного показателя. В первую очередь необходимо учитывать изменения количественных, а затем качественных показателей. Если же имеется несколько количественных и несколько качественных показателей, то сначала следует изменить величину факторов первого уровня подчинения, а потом более низкого.

2.2 Способ абсолютных разниц является алгебраическим упрощением метода цепных подстановок. Используется для расчета влияния факторов в мультипликативных моделях и моделях мультипликативно – аддитивного типа 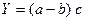и .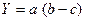

При его использовании величина влияния факторов рассчитывается умножением абсолютного прироста значения исследуемого фактора на базовую (плановую) величину факторов, которые находятся справа от него, и на фактическую величину факторов, расположенных слева от него в модели.

Исходная модель – мультипликативная

Исходная модель – мультипликативно- аддитивного типа .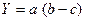

2.3 Способ относительных разниц – применяется для измерения влияния факторов на прирост результативного показателя только в мультипликативных моделях. Используются относительные приросты факторных показателей, выраженные в виде коэффициентов или процентов.

Исходная модель – мультипликативная . Для расчета влияния первого фактора необходимо базовую величину результативного показателя умножить на относительный прирост первого фактора, выраженного в виде десятичной дроби.

Для расчета влияния второго фактора нужно к базовой величине результативного показателя прибавить изменение его за счет первого фактора и затем полученную сумму умножить на относительный прирост второго фактора. Влияние третьего фактора определяется аналогично.

Изменения результативного показателя определяется следующим образом:

2.4 Интегральный метод – применяется для измерения влияния факторов в мультипликативных, кратных и кратно – аддитивных моделях. Его использование позволяет получать более точные результаты расчета влияния факторов по сравнению с ранее рассмотренными способами, поскольку дополнительный прирост результативного показателя от взаимодействия факторов присоединяется не к последнему фактору, а делится поровну между ними.

Исходная модель – мультипликативная

Исходная модель – мультипликативная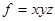

Достоинством метода является то, что не важен порядок написания факторов частных факторов в формуле результативного показателя.

2.5. Индексный метод: основан на применении индексов - относительных величин, характеризующих изменение экономических показателей во времени, либо в сравнении с планом или с другой базой. Индексы, выражающие соотношение непосредственно соизмеряемых величин, называются индивидуальными, а характеризующие соотношение сложных явлений – агрегатными. Как правило, в расчетах используются агрегатные индексы.

;

С помощью индексного метода оценивается изменение уровня явления (или относительного изменения показателя), выявляется роль отдельного фактора в изменении результативного показателя, оценивается влияние структуры совокупности на динамику среднего уровня анализируемого показателя и т.д.

При составлении агрегатного индекса необходимо учитывать следующее правило:

- при определении влияния количественного фактора качественный фиксируется на базисном уровне;

- при определении влияния качественного фактора количественный фиксируется на уровне отчетного года.

2.6 Способ пропорционального деления и долевого участия применяется для измерения влияния факторов в аддитивных и кратно – аддитивных моделях типа ;

Для модели типа , расчет производится следующим образом:

В моделях кратно-аддитивного вида сначала необходимо способом цепной подстановки определить, насколько изменился результативный показатель за счет числителя и знаменателя, а затем произвести расчет влияния факторов второго порядка способом пропорционального деления по вышеприведенным алгоритмам.

Для решения такого типа задач можно использовать также способ долевого участия. Для этого сначала определяется доля каждого фактора в общей сумме их приростов, которая затем умножается на общий прирост результативного показателя.

; ;

2.7 Способ логарифмирования – применяется для измерения влияния факторов в мультипликативных моделях. Как и при интегрировании, результат расчета не зависит от последовательности написания факторов в формуле результативного показателя. По сравнению с интегральным методом логарифмирование обеспечивает более высокую точность расчетов.

При логарифмировании используются индексы роста (снижения) показателей.

Исходная модель – мультипликативная 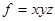. Влияние факторов определится следующим образом.

; ;

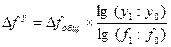Общий прирост результативного показателя распределяется по факторам пропорционально отношениям логарифмов факторных индексов к логарифму результативного показателя. Не имеет значения, какой логарифм используется – натуральный или десятичный. Преимущество способа логарифмирования состоит в относительной простоте вычислений и более высокой точности расчетов.