Задание для индивидуальной контрольной работы по дисциплине «Статистика»
Работа выполняется студентом на листах формата А4 (рукописный или печатный вариант) или в тетради с соблюдением требований ГОСТ к оформлению работ.
Если работа выполняется на листах формата А4, то должны быть выдержаны следующие поля: верхние и нижние – по 2 см, левое – 3 см, правое – 1 см.
Для работы, выполненной на компьютере, необходимо использовать шрифт Times New Roman, 14, интервал 1,5.
Если работа выполнена в тетради, то на каждой странице необходимо оставить поля 3 см для замечаний.
Работа выполняется по вариантам. Номер варианта соответствует последней цифре зачетной книжки. Если последняя цифра 0, то студент выполняет 10 вариант.
Задание 1
Объем выданных кредитов в 30 банках региона составили (млн руб.):
| Банк, № п/п | ||||||||||
| Сумма кредитов | Сумма кредитов | Сумма кредитов | Сумма кредитов | Сумма кредитов | Сумма кредитов | Сумма кредитов | Сумма кредитов | Сумма кредитов | Сумма кредитов | |
Произведите группировку банков по размеру кредита, образовав пять групп магазинов с равными интервалами. В каждой группе и в целом подсчитайте:
1) число банков;
2) размер кредита – всего и в среднем на один банк;
3) Решение оформите в разработочной и групповой таблицах. Сделайте выводы, укажите вид группировки. Постройте гистограмму и преобразуйте её в полигон. Постройте кумуляту (кривую накопленных частот).
Задание 2
Данные о производстве яиц в хозяйствах всех категорий области:
| Год | Произведено яиц, млн. шт. | |||||||||
| Вариант | ||||||||||
Определите:
1) вид динамического ряда;
2) средний уровень динамического ряда;
3) абсолютные приросты, темпы роста и прироста цепные и базисные, абсолютное содержание 1% прироста;
4) средний абсолютный прирост, средний темп роста и прироста уровней динамического ряда.
5) оцените наличие тренда.
Задание 3
Объем производства продукции и себестоимость единицы продукции на предприятии за два периода составили:
| Вариант | Наименование продукции | Себестоимость единицы продукции, руб. | Произведено продукции, тыс. шт. | ||
| Базисный период | Отчетный период | Базисный период | Отчетный период | ||
| А | |||||
| Б | |||||
| А | |||||
| Б | |||||
| А | |||||
| Б | |||||
| А | |||||
| Б | |||||
| А | |||||
| Б |
Определите:
1) индивидуальные индексы себестоимости и количества произведенной продукции;
2) общий индекс затрат на производство;
3) общий индекс себестоимости;
4) общий индекс физического объема произведенной продукции;
5) абсолютный размер изменения затрат производства – всего, в том числе за счет изменения себестоимости продукции и физического объема продукции.
Покажите взаимосвязь индексов. Сделайте выводы.
Задание 4
С целью изучения затрат времени на обслуживание одного клиента в кредитном отделе банка было проведено выборочное наблюдение. Результат наблюдения представлен в таблице.
| Затраты времени, мин. | Число кредитных инспекторов, чел | ||||
| Вариант | |||||
| До 5 | |||||
| 5-7 | |||||
| 7-9 | |||||
| 9-11 | |||||
| Свыше 11 |
Рассчитать:
· среднее время на обслуживание одного клиента;
· размах вариации;
· среднее линейное отклонение;
· дисперсию;
· среднее квадратическое отклонение;
· линейный коэффициент вариации;
· коэффициент вариации;
Сделать вывод об однородности статистической совокупности и о надежности средней величины.
Задание 5
Определите направление и тесноту связи между указанными в вашем варианте признаками. Предварительно проранжируйте ряды данных Х и У. Сопоставив полученные ряды, установите наличие зависимости между признаками:
1) Постройте уравнения регрессии.
2) Рассчитайте линейный коэффициент корреляции.
Сделайте выводы.
| Вариант | 1, 6 | 2, 7 | 3, 8 | 4, 9 | 5, 10 | |||||
| № предприятия | Цена за единицу товара, у.е. | Объём продаж тыс. у.е. | Цена за единицу товара, у.е. | Объём продаж тыс. у.е. | Цена за единицу товара, у.е. | Объём продаж тыс. у.е. | Цена за единицу товара, у.е. | Объём продаж тыс. у.е. | Цена за единицу товара, у.е. | Объём продаж тыс. у.е. |
Методические рекомендации по выполнению индивидуальной курсовой работы по дисциплине «Статистика»
Задание 1
Объем выданных кредитов в 30 банках региона составили (млн руб.):
| Банк, № п/п | Сумма кредита |
Произведите группировку банков по размеру кредита, образовав пять групп магазинов с равными интервалами. В каждой группе и в целом подсчитайте:
1) число банков;
2) размер кредита – всего и в среднем на один банк;
3) Решение оформите в разработочной и групповой таблицах. Сделайте выводы, укажите вид группировки. Постройте гистограмму и преобразуйте её в полигон. Постройте кумуляту (кривую накопленных частот).
Решение:
Составим вариационный ряд распределения, упорядочив магазины по товарообороту от меньшего к большему.
| Банк, № п/п | Кредит | Банк, № п/п | Кредит |
| 7 | 341 | ||
| 11 | 456 | 19 | 1199 |
| 5 | 1326 | ||
Определим величину интервала:
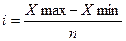, где
i – величина интервала;
n – число групп (в данной задаче 5 группы);
Xmax, Xmin – максимальное и минимальное значение признака (1700 и 341 соответственно).
Величина интервала составит:
Определим границы интервалов:
| Интервал | Нижняя граница | Верхняя граница |
| 1-й | 341 + 271,8 = 612,8 | |
| 2-й | 612,8 | 612,8 + 271,8 = 884,6 |
| 3-й | 884,6 | 884,6 + 271,8 = 1156,4 |
| 4-й | 1156,4 | 1556,4 + 271,8 = 1428,2 |
| 5-й | 1428,2 | 1428,2 + 271,8 = 1700 |
Разнесем по выделенным интервалам предприятия (разработочная таблица):
| Группы банков по величине кредитов | Номера банков | Число банков |
| 341-612,8 | 7,11 | |
| 612,8-884,6 | 21, 24, 17, 22, 25, 18 | |
| 884,6-1156,4 | 27, 12, 13, 1, 9, 14, 6, 15 | |
| 1156,4-1428,2 | 19, 5 | |
| 1428,2-1700 | 2, 30, 20, 16, 10, 29, 3, 28, 23, 4, 8, 26 |
Определим в каждой группе и в целом объем выданных кредитов – всего и в среднем на один банк, для чего составим группировочную таблицу:
| Группы банков по величине выданных кредитов | Число банков в группе | Доля банков, % | Суммарная величина кредита в группе | Доля по кредитам, % | Средний размер кредита по группе |
| А | (1) | (2) | (3) | (4) | (5)=(3)/(1) |
| 341-612,8 | 2 / 30 *100= 6,67 | 2,30 | 398,5 | ||
| 612,8-884,6 | 6 / 30*100= 20,00 | 12,88 | 744,5 | ||
| 884,6-1156,4 | 26,67 | 23,04 | 998,75 | ||
| 1156,4-1428,2 | 6,67 | 7,28 | 1262,5 | ||
| 1428,2-1700 | 40,00 | 54,50 | |||
| Итого | 100,00 | 100,00 | 34679/30= 1155,97 |
На основании проведенных расчетов построим гистограмму и полигон.
При построении гистограммы по оси Х откладывают значения признака (границы интервалов), а по оси Y – частоты. Для соответствующего интервала строиться прямоугольник, высота которого соответствует частоте признака (рисунок 1).
Объем выданных кредитов
Рисунок 1 – Гистограмма
Гистограмма может быть преобразована в полигон, если середины верхних граней прямоугольника соединить прямой линией (рисунок 2).
Объем выданных кредитов
Рисунок 2 – Полигон распределения
Также построим кумуляту или кривую накопленных частот. В этом случае по оси Х откладываем интервалы признака, а по оси Y – накопленные частоты (это количество единиц совокупности, имеющие значения признака меньше указанного. Накопленные частоты рассчитаны в таблице.
| Группы предприятий по величине оборота | Число предприятий в группе | Накопленные частоты |
| 341-612,8 | ||
| 612,8-884,6 | ||
| 884,6-1156,4 | ||
| 1156,4-1428,2 | ||
| 1428,2-1700 |
Кривая накопленных частот представлена на рисунке 3.
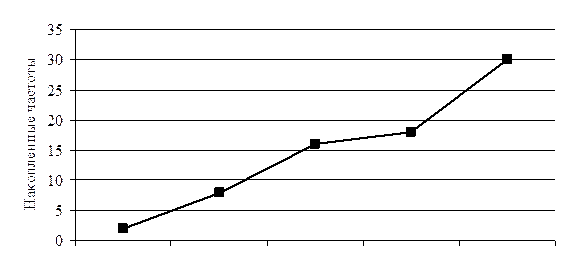
Объем выданных кредитов
Рисунок 3 – Кривая накопленных частот
Вывод: Суммарный объем выданных кредитов в первой группе 797 млн. руб., во второй – 4467 млн. руб., в третьей – 7990 млн. руб., в четвертой – 2525 млн. руб., в пятой – 18900 млн. руб. Средняя величина выданных кредитов на один банк в первой группе 398,5 млн. руб., во второй – 744,5 млн. руб., в третьей – 998,75 млн. руб., в четвертой – 1262,5 млн. руб., в пятой – 1575 млн. руб.
Задание 2
Данные о производстве яиц в хозяйствах всех категорий области:
| Год | |||||||||
| Произведено яиц, млн. шт. |
Определите:
1) вид динамического ряда;
2) средний уровень динамического ряда;
3) абсолютные приросты, темпы роста и прироста цепные и базисные, абсолютное содержание 1% прироста;
4) средний абсолютный прирост, средний темп роста и прироста уровней динамического ряда;
5) оцените наличие тренда.
Решение:
Данный ряд является рядом интервальным (отражает развитие явление за год). Динамический ряд состоит из абсолютных величин.
Определим средний уровень ряда по формуле средней арифметической простой:
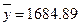млн. шт.
Алгоритм расчета показателей динамики представлен в следующей таблице.
| Показатель | Базисный | Цепной |
| Абсолютный прирост (∆) | Yi-Y0 | Yi-Yi-1 |
| Коэффициент роста (Кр) | Yi : Y0 | Yi: Yi-1 |
| Темп роста (Тр) | (Yi : Y0)×100 | (Yi : Yi-1)×100 |
| Темп прироста (Тпр) | Тр-100 | Тр-100 |
| Абсолютное значение 1% прироста | Y0 / 100 | Δ / Тпр |
В случае, когда сравнение проводится с периодом (моментом) времени, начальным в ряду динамики (Y0), получают базисные показатели. Если же сравнение производится с предыдущим периодом или моментом времени, то говорят о цепных показателях.
Рассчитаем указанные показатели для данной задачи:
| Показатель | |||||||||
| Производство яиц, млн. шт. | |||||||||
| Абсолютный прирост (∆), млн. яиц | |||||||||
| Базисный | - | 1558-1842= -284 | 1629-1842= -213 | 1617-1842= -225 | 1585-1842= -257 | 1722-1842= -120 | -25 | -23 | -267 |
| Цепной | - | 1558-1842= -284 | 1629-1558=71 | 1617-1629= -12 | 1585-1617= -32 | 1722-1585=137 | -244 | ||
| Коэффициент роста (Кр) | |||||||||
| Базисный | - | 1558/ 1842= 0,8458 | 1629/ 1842= 0,8844 | 1617/ 1842= 0,8779 | 1585/ 1842= 0,8605 | 1722/ 1842= 0,9349 | 0,9864 | 0,9875 | 0,8550 |
| Цепной | - | 1558/ 1842= 0,8458 | 1629/ 1558= 1,0456 | 1617/ 1629= 0,9926 | 1585/ 1617= 0,9802 | 1722/ 1585= 1,0864 | 1,0552 | 1,0011 | 0,8659 |
| Темп роста (Тр), % (Кр * 100) | |||||||||
| Базисный | - | 0,8458*100=84,58 | 0,8844*100=88,44 | 87,79 | 86,05 | 93,49 | 98,64 | 98,75 | 85,50 |
| Цепной | - | 84,58 | 104,56 | 99,26 | 98,02 | 108,64 | 105,52 | 100,11 | 86,59 |
| Темп прироста (Тпр), % (Тр – 100) | |||||||||
| Базисный | - | 84,58-100 = -15,42 | 88,44-100= -11,56 | -12,21 | -13,95 | -6,51 | -1,36 | -1,25 | -14,50 |
| Цепной | - | -15,42 | 4,56 | -0,74 | -1,98 | 8,64 | 5,52 | 0,11 | -13,41 |
| Абсолютное значение 1% прироста | |||||||||
| Базисный | - | -284/ (-15,42) = 18,42 | -213/ (-11,56) = 18,42 | -225/ (-12,21) = 18,42 | -257/ (-13,95) = 18,42 | -120/ (-6,64) = 18,42 | 18,42 | 18,42 | 18,42 |
| Цепной | - | -284/ (-15,42) = 18,42 | 71/ (4,56) = 15,58 | -12/ (-0,74) = 16,29 | -32/ (-1,98) = 16,17 | 137/ (8,64) = 15,85 | 17,22 | 18,17 | 18,19 |
Рассчитаем средние показатели:
А) средний абсолютный прирост: 
млн. яиц
Б) Средний темп роста:
В) Средний темп прироста: 98,06 – 100 = -1,94%
Таким образом, объем производства яиц в 2007 по сравнению с 2006 годом сократился на 15,42% или на 284 млн. шт., при этом в 2008 по сравнению с 2006 – увеличился на 4,56% или на 71 млн. В 2009 по сравнению с 2008 объем производства сократился на 0,74% или на 12 млн. шт., а в 2010 по сравнению с 2009 – на 1,98% или на 32 млн. шт. В 2011 по сравнению с 2010 годом объем производства увеличился на 8,64% или на 137 млн. шт., а в 2012 по сравнению с 2011 – на 5,52% или на 95 млн. шт. В 2013 по сравнению с 2012 годом объем производства увеличился на 0,11% или на 2 млн. шт., а в 2014 по сравнению с 2013 – уменьшился на 13,41% или на 244 млн. шт. В среднем за 8 лет производство яиц ежегодно снижалось на 33,375 млн. шт. (или на 1,94% в год). По сравнению с 2006 годом объем производства в 2014 году сократился на 14,50%.
Выявление тенденции
Метод укрупнения интервалов основан на том, что у исследуемого временного интервала расширяются временные рамки (дни объединяются в декады, месяцы в кварталы и т.д.)
В рамках данной задачи расширим временные рамки до двух лет. Полученные результаты представлены в таблице.
| Год | Произведено яиц, млн. шт. | Всегопроизведено яиц, млн. шт.за три года |
| 1842+1558+1629= | ||
| 1617+1585+1722= | ||
| 1817+1819+1575= | ||
По полученным данным видно, тенденция не выявлена.
При изучении тенденции (основного направления развития явления) методом скользящей средней рассчитывают среднее значение за три периода: анализируемый период, период до него и после. Таким образом, скользящей средней нет для первого и для последнего периода, т.к.
Расчет скользящей средней за три года представлен в таблице.
| Год | Произведено яиц, млн. шт. | Скользящая средняя за три года |
| - | ||
| (1842+1558+1629)/3 = 1676,333 | ||
| (1558+1629+1617)/3 = 1601,333 | ||
| (1629+1617+1585)/3 = 1610,333 | ||
| 1641,333 | ||
| (1817 + 1819 +1575) / 3 = 1737 | ||
| - |
Задача измерения тренда измеряется методом аналитического выравнивания. При его применении тренд рассчитывается как некоторая функция от времени 
Используем линейную модель для построения уравнения 
.
Для вычисления параметров функции методов наименьших квадратов составляем систему уравнений:
С целью упрощения расчетов на практике рекомендуют применять способ расчета времени от условного начала. Этот способ основан на обозначении показателей времени таким образом, чтобы сумма времени (Σt) была равна нулю. Тогда для функции , будет:
Для определения этих параметров построим вспомогательную таблицу.
| Год | Производство яиц, млн. шт. | t | t2 | y×t | уt |
| -4 | -7368 | 1671,82 | |||
| -3 | -4674 | 1675,09 | |||
| -2 | -3258 | 1678,36 | |||
| -1 | -1617 | 1681,62 | |||
| 1684,89 | |||||
| 1688,16 | |||||
| 1691,42 | |||||
| 1694,69 | |||||
| 1697,96 | |||||
| Итого |
Отсюда,
Уравнение прямой будет иметь вид: уt = 1684,89 + 3,27×t.
Таким образом, каждый год производство яиц увеличивается на 3,27 млн. шт.
Задание 3
Производство продукции и ее себестоимость на предприятии за два периода составили:
| Наименование продукции | Себестоимость единицы продукции, руб. | Произведено продукции, тыс. шт. | ||
| Базисный период | Отчетный период | Базисный период | Отчетный период | |
| А | ||||
| Б |
Определите:
1) индивидуальные индексы себестоимости и количества произведенной продукции;
2) общий индекс затрат на производство;
3) общий индекс себестоимости;
4) общий индекс физического объема произведенной продукции;
5) абсолютный размер изменения затрат производства – всего, в том числе за счет изменения себестоимости продукции и физического объема продукции.
Покажите взаимосвязь индексов. Сделайте выводы.
Решение:
Индивидуальный индекс себестоимости определяется отдельно по каждому виду продукции и рассчитывается по формуле: 
, где z0 и z1 – себестоимость в базисном и отчетном году соответственно.
Индивидуальные индексы количества произведенной продукции составят: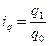 
, где q0 и q1 – количество произведенной продукции в товарных единицах в базисном и отчетном году соответственно.
Индивидуальный индекс затрат на производство определяется также отдельно по каждому виду продукции и рассчитывается по формуле: 
,
Индивидуальные индексы рассчитаны в таблице.
| Наименование продукции | Себестоимость единицы продукции, тыс. шт. | Произведено продукции, руб. | Общие затраты, тыс. руб. | Индивидуальные индексы | |||||
| Базисный z0 | Отчетный z1 | Базисный q0 | Отчетный q1 | Базисный q0*z0 | Отчетный q1*z1 | себестоимости z1 / z0 | объема производства q1 / q0 | Общих затрат q1*z1 / q0*z0 | |
| А | 82*121= | 105*97= | 105/82= 1,280 | 97/121= 0,802 | 10185/ 9922= 1,027 | ||||
| Б | 110*86= | 97*132= | 97/110= 0,882 | 132/86= 1,535 | 12804/ 9460= 1,353 |
Между рассчитанными индексами признаками существует взаимосвязь. Она называется мультипликативная факторная индексная модель:
;
Например, по продукции А: 1,280*0,802= 1,027
По продукции Б: 0,882*1,535=1,353
Таким образом, производство продукции А снизилось в отчетном году по сравнению с базисным на 19,8% (0,802*100-100), произошло увеличение объемов производства продукции Б в 1,535 раз или на 53,5% (1,535*100-100)
Себестоимость продукции А увеличилась в отчетном году по сравнению с базисным в 1,28 раза или на 28%, по группе Б себестоимость снизилась на 11,8%.
Общие затраты на производство продукции А увеличились в отчетном году по сравнению с базисным в 1,027 раза или на 2,7%, по группе Б – в 1,353 раза или на 35,3%.
Общий индекс затрат на производство показывает изменение объема произведенной продукции в целом по предприятию, в целом по всем группам товаров и определяется по формуле: 
.
Общий индекс себестоимости определяется по формуле: 
Общий индекс физического объема производства: 
.
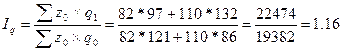
Здесь также между индексами существует взаимосвязь:
.
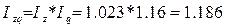Общие затраты на производство в целом по предприятию увеличились на 18,6% или в 1,186 раза. Общие затраты предприятия увеличились на 16% или в 1,16 раза за счет роста объемов производства продуктов. При этом общие затраты выросли на 2,3% в результате изменения себестоимости продукции.
Абсолютное изменение затрат на производство составит: 
тыс. руб.
Влияние на прирост затрат на производство продукции изменения количества произведенных товаров в абсолютной величине составит:
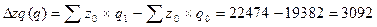тыс. руб.
Остальное изменение затрат на производство продукции связано с изменением себестоимости продукции:
тыс. руб.
Взаимосвязь между абсолютными приростами называется аддитивной факторной моделью: 
тыс. руб.
Вывод: Таким образом, производство продукции А снизилось в отчетном году по сравнению с базисным на 19,8% (0,802*100-100), произошло увеличение объемов производства продукции Б в 1,535 раз или на 53,5% (1,535*100-100)
Себестоимость продукции А увеличилась в отчетном году по сравнению с базисным в 1,28 раза или на 28%, по группе Б себестоимость снизилась на 11,8%, по группе В снижение составило8,7%.
Общие затраты на производство продукции А увеличились в отчетном году по сравнению с базисным в 1,027 раза или на 2,7%, по группе Б – в 1,353 раза или на 35,3%.
Общие затраты на производство в целом по предприятию увеличились на 18,6% или в 1,186 раза. Общие затраты предприятия увеличились на 16% или в 1,16 раза за счет роста объемов производства продуктов. При этом общие затраты выросли на 2,3% в результате изменения себестоимости продукции.
Общие затраты на производство в целом по предприятию увеличились на 3607 тыс. руб. Общие затраты предприятия увеличились на 3092 тыс. руб. за счет роста объемов производства продуктов. При этом общие затраты выросли на 515 тыс. руб. в результате снижения себестоимости продукции.
Задание 4
С целью изучения затрат времени на обслуживание одного клиента в банке было проведено выборочное наблюдение. Результат наблюдения представлен в таблице.
| Затраты времени, мин. | Число кредитных инспекторов, чел |
| До 5 | |
| 5-7 | |
| 7-9 | |
| 9-11 | |
| Свыше 11 |
Рассчитать:
· среднее время на обслуживание одного покупателя;
· размах вариации;
· среднее линейное отклонение;
· дисперсию;
· среднее квадратическое отклонение;
· линейный коэффициент вариации;
· коэффициент вариации;
· моду и медиану;
· с вероятностью 0,954 определите среднюю продолжительность разговора, если было обследовано 50% всех клиентов (бесповторный отбор).
Сделать вывод об однородности статистической совокупности и о надежности средней величины.
Решение:
1. В данном случае необходимо вычислить среднюю интервального ряда. Поэтому в качестве значения признаков в группах принимаются середины интервалов (простая средняя между верхней и нижней границей каждого интервала), в результате чего образуется дискретный ряд.
Если имеются интервалы с открытыми границами (в данной задаче это первый и последний интервал), то для расчета средней в этих условиях условно определяют неизвестную границу интервала. Обычно в этих условиях берут значение последующего интервала (для первого) или предыдущего (для последнего).
С учетом этих замечаний рассчитаем среднюю оценку по формуле средней арифметической взвешенной (т.к. каждое значение признака в исследуемой совокупности встречается неодинаковое число раз)
, где
xi – значение признака;
fi – частота
Данные для расчета среднего времени обслуживания клиентов представлены в таблице.
| Затраты времени, мин. | Величина признака (хi) | Число кредитных инспекторов,, чел. | xi ×fi | Накопленные частоты |
| До 5 Условный интервал 3-5, т.к. величина второго интервала 2 | (3+5) / 2 = 4 | |||
| 5-7 | (5+7) /2 = 6 | 3+5=8 | ||
| 7-9 | 8+11=19 | |||
| 9-11 | ||||
| Свыше 11 Условный интервал 11-13, т.к. величина предпоследнего интервала 2 | (11+13)/2=12 | |||
| ИТОГО | - |
Тогда время обслуживания клиента составит:
минут
2. Мода – наиболее часто встречающееся значение признака у единиц данной совокупности. Мода применяется при изучении качества продукции, покупательского спроса, конструировании одежды, обуви и т. д.
Медиана – варианта, делящая ранжированный ряд на две равные части.
В интервальном ряду распределения сразу можно указать только интервал, в котором будет находиться мода или медиана.
Для определения их величины используется следующие формулы:
, где
XM0 – начало модельного интервала;
h – величина модального интервала;
- частота, соответствующая модельному интервалу;
- предмодельная частота;
- послемодельная частота;
В дискретном вариационном ряду мода – это вариант с наибольшей частотой.
В интервальном ряду модой приближенно считают центральный вариант модального интервала, т.е. интервала с наибольшей частотой.
Мода составит (модальный интервал – от 9 до 11 – максимальная частота 27):
10,28 минут.
Таким образом, 10,28 минут чаще всего тратят продавцы на обслуживание клиента.
Для определения медианы используют формулу:
;
- нижняя граница медианного интервала;