Задание 1
С целью изучения затрат времени на обслуживание одного покупателя в магазине бытовой техники было проведено выборочное наблюдение. Результат наблюдения представлен в таблице.
| Затраты времени, мин. | Число продавцов, чел |
| До 5 | |
| 5-7 | |
| 7-9 | |
| 9-11 | |
| Свыше 11 |
Рассчитать: среднее время на обслуживание одного покупателя; размах вариации; среднее квадратическое отклонение; коэффициент вариации.
Сделать вывод об однородности статистической совокупности и о надежности средней величины.
Решение:
В данном случае необходимо вычислить среднюю интервального ряда. Поэтому в качестве значения признаков в группах принимаются середины интервалов (простая средняя между верхней и нижней границей каждого интервала), в результате чего образуется дискретный ряд.
Если имеются интервалы с открытыми границами (в данной задаче это первый и последний интервал), то для расчета средней в этих условиях условно определяют неизвестную границу интервала. Обычно в этих условиях берут значение последующего интервала (для первого) или предыдущего (для последнего).
С учетом этих замечаний рассчитаем среднюю оценку по формуле средней арифметической взвешенной (т.к. каждое значение признака в исследуемой совокупности встречается неодинаковое число раз)
где xi – значение признака;
fi – частота
Вариация признака – различие индивидуальных значений признака внутри совокупности. Она возникает в результате того, что индивидуальные значения признака складываются под совокупным влиянием разнообразных факторов, которые по-разному сочетаются в каждом конкретном случае.
Средняя величина – обобщающий показатель совокупности, она не показывает строение совокупности, не дает представления о том, как отдельные значения изучаемого признака группируются вокруг средней, сосредоточены ли они вблизи или значительно отклоняются от неё. Для изучения величины отклонений применяют показатели вариации.
|
|
1) Размах вариации – наиболее простой измеритель вариации и представляет собой разность между наибольшим (Xmax) и наименьшим (Xmin) значением признака:
Величина R показывает в каких пределах колеблется размер признака. Показатель указывает на общие размеры вариации, но не дает представления о степени колеблемости внутри совокупности. С помощью размаха вариации определяют допустимые размеры колебаний.
2) Среднее квадратичное отклонение равно корню квадратному из суммы квадратов отклонений индивидуальных значений признака от их средней, т.е. из дисперсии:
,
где G2 – дисперсия, определяемая по формуле:
- для простых величин;
- для взвешенных величин.
Чем меньше оно, тем лучше среднее значение отражает собой представленную совокупность.
На основании вышеперечисленных показателей вариации рассчитывается показатели относительного рассеивания, а именно коэффициент вариации – процентное соотношение среднего квадратического отклонения к средней величине:
.
Чем больше величина коэффициента вариации, тем больше разброс значений вокруг средней, тем менее однородна совокупность по своему составу и тем менее представительна средняя. Если V превышает 40%, то середина рассчитана по неоднородной совокупности и не будет являться типичной для данной совокупности.
|
|
Данные для расчета средней величины, размаха вариации, среднего квадратического отклонения и коэффициента вариации представлены в таблице.
| Затраты времени, мин. | Величина признака (хi) | Число продавцов, (fi) | xi ×fi | (xi – хср) | (xi – хср)2 | (xi – хср)2×fi |
| До 5 | (3+5) / 2 = 4 | -5,625 | 31,64 | 94,92 | ||
| 5-7 | (5+7)/2 = 6 | -3,625 | 13,14 | 65,70 | ||
| 7-9 | -1,625 | 2,64 | 29,05 | |||
| 9-11 | 0,375 | 0,14 | 3,80 | |||
| Свыше 11 | (11 + 13)/2=12 | 2,375 | 5,64 | 101,53 | ||
| Итого | - | - | - |
Непосредственно расчет средней величины, размаха вариации, среднего квадратического отклонения и коэффициента вариации представлены в таблице.
| Показатель | Формула расчета | Значение |
| Средние затраты времени, мин |
|  = 9,625
|
| Среднее квадратическое отклонение | 
|  = 2,15
|
| Коэффициент вариации | 
|  = 22,31
|
| Размах вариации | 
| 12 – 4 = 8 |
Вывод: средние затраты времени на обслуживание одного покупателя в магазинах бытовой техники составляют 9,625 минут. При этом время на обслуживание клиентов может колебаться от 4 до 12 минут (т.е. допустимый размах колебаний составляет 8 минут). Данная совокупность является однородной: значение коэффициента вариации (22%) не превышает пороговое значение в 40%.
Таким образом, рассчитанное среднее время на обслуживание одного клиента является типичной для данной совокупности.
Задание 2
Имеются данные о численности работников предприятия на начало каждого квартала года. Определить средние характеристики динамического ряда: средний уровень ряда (средняя численность работников), средний абсолютный прирост и средний темп роста и прироста. Указать виды средних, которые были использованы.
|
|
| Кварталы | Первый | Второй | Третий | Четвертый | Первый следующего года |
| Численность работников на начало квартала, чел. |
Решение:
1. Определим среднюю численность работников по средней хронологической, т.к. известны данные на начало каждого квартала (это моментный временной ряд):
,
где Т1, Т2, Т3, Т4, Т5 – численность работников на начало каждого квартала;
n – число кварталов.
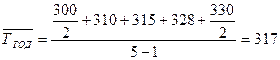чел.
Таким образом, средняя численность работников по предприятию в течение года составила 317 человек.
Задание 3
Данные по предприятиям объединения, выпускающим однородную продукцию, за два периода:
| Предприятие | Базисный период | Отчетный период | ||
| Затраты времени на единицу продукции, ч (xi) | Произведено продукции, тыс. шт. (fi) | Затраты времени на единицу продукции, ч (xi) | Затраты времени на всю продукцию, тыс. ч (Wi) | |
| 1-е | ||||
| 2-е | ||||
| 3-е |
Рассчитайте затраты времени на производство единицы продукции в среднем по объединению за каждый период. Обоснуйте применение формул средних для расчета заданных показателей. Сделайте выводы.
Решение:
Средние затраты времени на производство единицы продукции определяются как отношение затрат времени на производство всей продукции к объему произведенной продукции.
Затраты на производство всей продукции определяются как произведение количества произведенной продукции (частоты) и времени, которое затрачивает на производство единицы продукции (признак).
Для расчета средних затрат времени на производство единицы продукции в базисном можно использовать формулу средней арифметической взвешенной. Здесь выделен признак и его частота, и признак в исследуемой совокупности встречается неодинаковое число раз. Кроме того, в логической формуле средней не известен числитель.
, где
xi – значение признака;
fi – частота.
Средние затраты времени на производство единицы продукции в базисном периоде составят:
часа
Затраты на производство всей продукции определяются как произведение количества произведенной продукции и времени, которое затрачивает на производство единицы продукции. В этом случае в формуле расчета средней не известен знаменатель, поэтому логично использовать формулу средней гармонической.
3,34 часа
Вывод: Средние затраты времени на производство единицы продукции в базисном периоде составили 3,87 часа, в отчетном – 3,34 часа. Таким образом, средние затраты времени на производство единицы продукции сократились на 0,53 часа.
Индексы
Задание 1
Имеются следующие данные о продаже товаров в магазине:
| Товарные группы | Продано, кг | Цена за 1 кг, руб. | ||
| Базисный период | Отчетный период | Базисный период | Отчетный период | |
| А | ||||
| Б | ||||
| В |
Определите:
1) индивидуальные индексы цен и физического объема продаж;
2) общий индекс цен;
3) общий индекс физического объема продаж;
4) общий индекс оборота в действующих ценах;
5) абсолютную сумму прироста оборота – всего, в том числе за счет изменения цен и количества проданных товаров.
Сделайте выводы.
Решение:
Индивидуальный индекс объема продукции определяется отдельно по каждому виду продукции и рассчитывается по формуле:
,
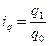где q0 и q1 – количество реализованной продукции в товарных единицах в базисном и отчетном году соответственно.
Индивидуальные индексы цен по каждому виду продукции составят:
где р0 и р1 – цена реализованной продукции в базисном и отчетном году соответственно.
Индивидуальный индекс товарооборота (стоимости) определяется также отдельно по каждому виду продукции и рассчитывается по формуле:
,
Индивидуальные индексы рассчитаны в таблице.
| Товарные группы | Продано, кг | Цена за 1 кг, руб. | товарооборот, руб. | индивидуальные индексы | |||||
| Базисный q0 | Отчетный q1 | Базисный p0 | Отчетный p1 | Базисный q0*p0 | Отчетный q1*p1 | объема продаж q1 / q0 | Цены p1 / p0 | товарооборота q1*p1 / q0*p0 | |
| А | 220/200 =1,10 | 1,22 | 1,34 | ||||||
| Б | 0,93 | 1,27 | 1,18 | ||||||
| В | 1,04 | 1,14 | 1,18 |
Таким образом, выпуск продукции по группе А увеличился в отчетном году по сравнению с базисным в 1,1 раза или на 10%, по группе Б произошло снижение объема реализованной продукции на 7% (0,93*100-100), по группе В – увеличение на 4%.
Цена продукции по группе А увеличилась в отчетном году по сравнению с базисным в 1,22 раза или на 22%, по группе Б – в 1,27 раза или на 27%, по группе В – в 1,14 раза или на 14%.
Товарооборот по товарной группе А увеличился в отчетном году по сравнению с базисным в 1,34 раза или на 34%, по группе Б – в 1,18 раза или на 18%, по группе В – в 1,18 раза или на 18%.
Общий индекс товарооборота или стоимости показывает изменение объема реализованной продукции в целом по предприятию, в целом по всем группам товаров и определяется по формуле:
,
Общий индекс цен определяется по формуле:
Общий индекс физического объема определяется как:
,
Абсолютное изменение товарооборота: 
;
Влияние на прирост товарооборота изменения количества проданных товаров в абсолютной величине составит:
Остальное изменение товарооборота связано с изменением цен на товар:
Для расчета этих показателей построим вспомогательную таблицу:
| Товарные группы | Продано, кг | Цена за 1 кг, руб. | товарооборот, руб. | ||||
| Базисный период | Отчетный период | Базисный период | Отчетный период | Базисный период q0*p0 | Отчетный период q1*p1 | отчетный в ценах базисного периода q1*p0 | |
| А | 3960,00 | ||||||
| Б | 4200,00 | ||||||
| В | 5720,00 | ||||||
| Итого |
Общий индекс товарооборота составит:
,
Товарооборот в целом по предприятию увеличился на 22,5% или в 1,225 раза.
Общий индекс цен составит:
Товарооборот предприятия увеличился на 20% или в 1,2 раза за счет роста цен на товар.
Общий индекс физического объема составит:
Товарооборот предприятия увеличился на 2% или в 1,02 раза за счет роста объема продаж.
Абсолютное изменение товарооборота составит: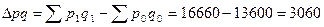 
рублей;
Влияние на прирост товарооборота изменения количества проданных товаров в абсолютной величине составит:
рублей
Остальное изменение товарооборота связано с изменением цен на товар:
рублей.
Вывод: Таким образом, выпуск продукции по группе А увеличился в отчетном году по сравнению с базисным в 1,1 раза или на 10%, по группе Б произошло снижение объема реализованной продукции на 7% (0,93*100-100), по группе В – увеличение на 4%.
Цена продукции по группе А увеличилась в отчетном году по сравнению с базисным в 1,22 раза или на 22%, по группе Б – в 1,27 раза или на 27%, по группе В – в 1,14 раза или на 14%.
Товарооборот по товарной группе А увеличился в отчетном году по сравнению с базисным в 1,34 раза или на 34%, по группе Б – в 1,18 раза или на 18%, по группе В – в 1,18 раза или на 18%.
Товарооборот в целом по предприятию увеличился на 22,5% или в 1,225 раза. Товарооборот предприятия увеличился на 20% или в 1,2 раза за счет роста цен на товар и увеличился на 2% или в 1,02 раза за счет роста объема продаж.
Абсолютное изменение товарооборота составило 3060 рублей, в том числе за счет изменения цен – на 2780 рублей и за счет изменения количества проданных товаров – на 280 рублей.
Задание 2
В городе 2 завода производят один и тот же вид продукции. Выпуск продукции и ее себестоимость за два периода характеризуются следующими данными:
| Завод | Себестоимость единицы продукции, руб. | Выпуск продукции, шт. | ||
| базисный период | отчетный период | базисный период | отчетный период | |
Определить:
1. Изменение себестоимости одной штуки в отчетном периоде по сравнению с базисным на каждом заводе и в среднем по заводам (в %).
2. Индексы средней себестоимости постоянного состава и структурных сдвигов. Пояснить экономический смысл рассчитанных индексов.
3. Изменение затрат на производство продукции по совокупности заводов (в абсолютном выражении) в целом, а также за счет изменения: а) количества произведенной продукции; б) среднего уровня себестоимости единицы продукции; в) собственно самой себестоимости по отдельным заводам;
г) удельного веса продукции, произведенной на заводах с разным уровнем себестоимости единицы продукции.
Проверить увязку полученных результатов в систему. Сделать выводы.
Решение:
Изменение себестоимости на каждом заводе отражает индивидуальный индекс себестоимости:
где z0 и z1 – себестоимость продукции в базисном и отчетном году соответственно.
Изменение себестоимости на заводе №1: 
, т.е. себестоимость единицы продукции сократилась на 14,2% (0,858*100 – 100).
Изменение себестоимости на заводе №2: 
, т.е. себестоимость единицы продукции сократилась на 10% (0,9*100 – 100).
Индекс переменного состава показывает, как изменяется средняя себестоимость в отчетном году по сравнению с базисным по двум заводам и рассчитывается по формуле:
,
где q0 и q1 – выпуск продукции в базисном и отчетном году соответственно.
Средняя себестоимость по двум заводам сократилась на 15,6%.
Индекс постоянного состава определяет изменение себестоимости товара в результате изменения себестоимости по каждому заводу:
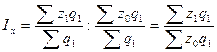
Средняя себестоимость товара из-за изменения себестоимости на двух заводах снизилась на 11,96%.
В индексе структурных сдвигов учитывается влияние структурных изменений в составе совокупности (т.е. изменение структуры производства по заводам):
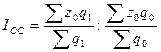
Средняя себестоимость продукции на двух заводах в результате изменения структуры производства на заводах снизилась на 4,17 % (0,9583 *100 – 100=-4,17%).
Указанные выше индексы связаны между собой:
Iпер. = Iпост. × Iсс
0,844 = 0,8804 * 0,9583
Определим изменение затрат на производство продукции по совокупности заводов (в абсолютном выражении) в целом. Изменение составит:
руб.
Совокупные затраты по двум заводам сократились на 7500 рублей.
Рассчитаем изменение затрат за счет изменения:
а) количества произведенной продукции:
тыс. руб.
б) среднего уровня себестоимости единицы продукции:
тыс. руб.
в) собственно самой себестоимости по отдельным заводам:
тыс. руб.
г) удельного веса продукции, произведенной на заводах с разным уровнем себестоимости единицы продукции:
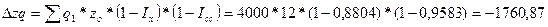тыс. руб.
Проверка: -5739,13 + (-1760,87) = -7500 тыс. руб.
-7500 + 0 = - 7500 тыс. руб.
Вывод: себестоимость единицы продукции сократилась на 14,2%, себестоимость единицы продукции сократилась на 10%.
Средняя себестоимость по двум заводам сократилась на 15,6%. Средняя себестоимость товара из-за изменения себестоимости на двух заводах снизилась на 11,96%. Средняя себестоимость продукции на двух заводах в результате изменения структуры производства на заводах снизилась на 4,17 %.
Совокупные затраты по двум заводам сократились на 7500 рублей.
Это изменение связано с изменением средней себестоимости, т.е. объем производства в штуках не изменился и составил 4000 рублей, но при этом изменилась структура производства. В результате совокупные затраты сократились на 1760,87 тыс. руб. Из-за изменения себестоимости на каждом из заводов себестоимость сократилась на 5739,13 тыс. руб.
Задание 3
Имеются следующие данные о товарообороте магазина потребительской кооперации:
| Товарная группа | Продано товаров в фактических ценах, млн. руб. | Индексы цен в 2011г. по сравнению с 2010г. iр | |
| 2010 г. (р0q0) | 2011 г (р1q1) | ||
| Трикотажные изделия | 340,5 | 371,1 | 1,02 |
| Чулочно-носочные изделия | 160,7 | 186,3 | 0,97 |
Вычислите:
1) общий индекс товарооборота в фактических ценах;
2) общий индекс цен;
Общий индекс физического объема продажи товаров используя взаимосвязь индексов.
Как повлияло изменение цен на величину товарооборота в 2010 году?
Решение:
Общий индекс товарооборота показывает изменение товарооборота в целом по предприятию и определяется по формуле:
,
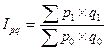где р0q0 – товарооборот базисного года;
р1q1 – товарооборот отчетного года
Товарооборот предприятия вырос на 11,21% (1,1121*100-100).
Общий индекс цен определяется по формуле:
,
где р1q1 – товарооборот отчетного года;
р0q1 – товарооборот в ценах базисного периода (эти данные по условию задачи отсутствуют).
Но формулу общего индекса цен можно преобразовать с помощью индивидуальных индексов цен. Для этого выразим р0 через р1 и iр.
Товарооборот предприятия вырос на 0,27% за счет изменения цены товаров (1,0027*100-100).
Общий индекс физического объема продаж определяется на основе следующей взаимосвязи:
.
Товарооборот предприятия вырос на 10,91% за счет изменения объемов продаж.
Абсолютное изменение товарооборота составит:
млн. руб.
Влияние на прирост товарооборота изменения цен продукции определяется по формуле:
млн. руб.
Остальное изменение товарооборота связано с изменением объема реализации.
Вывод: Товарооборот предприятия вырос на 11,21%. Товарооборот предприятия вырос на 0,27% за счет изменения цены товаров. Товарооборот предприятия вырос на 10,91% за счет изменения объемов продаж.
Товарооборот вырос на 56,2 млн. рублей. В том числе за счет изменения цен на товары товарооборот вырос на 1,51 млн. руб.
Ряды динамики
Задание 1
Используя базу данных Федеральной службы государственной статистики (www.gks.ru), постройте ряд динамики за последние 8-10 лет по любому из показателей. Проанализируйте данные. Для этого:
1) определите все возможные цепные, базисные и средние показатели анализа ряда динамики;
2) произведите сглаживание уровней временного ряда методами укрупнения интервалов, скользящей средней и аналитического выравнивания (интервал укрупнения и период скольжения определите самостоятельно).
Сделайте выводы.
Решение:
Проанализируем динамику экспорта в России по данным представленным в таблице.