В АлтГТУ принята 100-балльная шкала оценок. Именно эти оценки учитываются при подсчёте рейтингов, назначении стипендий и в других случаях. Традиционная шкала будет использоваться только в зачётных книжках. Соответствие оценок устанавливается следующим образом:75 баллов и выше – «отлично», 50-74 балла – «хорошо», 25-49 баллов – «удовлетворительно», менее 25 баллов – «неудовлетворительно».
Успеваемость студента оценивается с помощью текущего рейтинга (во время каждой аттестации) и итогового рейтинга (после сессии).
Текущий рейтинг (во время каждой аттестации) учитывает оценки за контрольные точки, выполнение ИДЗ, оценки за коллоквиумы, работу на занятиях.
Итоговый рейтинг (после сессии) вычисляется по формуле: 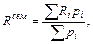
где 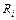 – оценка за i-ю контрольную работу,
– оценка за i-ю контрольную работу, 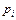 – вес этой контрольной работы.
– вес этой контрольной работы.
Приведём пример. Пусть студент получил оценки: КР по теме 1 – 30 баллов, КР по теме 2 – 40 баллов, ИДЗ – 50 баллов, зачёт – 50 баллов.
На 1-й аттестации (7 неделя) его рейтинг равен: 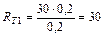 .
.
На 2-й аттестации (13 неделя): 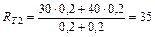 .
.
Перед началом сессии вычисляется семестровый рейтинг:
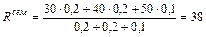 .
.
Итоговый рейтинг, учитывающий зачёт (экзамен): 
ПАМЯТКА за III семестр ПО ДИСЦИПЛИНЕ
«Математика» для студентов направления
«Конструкторско-технологическое обеспечение машиностроительных производств»
Факультет инновационных технологий машиностроения
Содержание дисциплины
10 Интегральное исчисление функций нескольких переменных - 12ч. [1,2,5,6,7,8]
Вычисление двойных интегралов в декартовых координатах, полярных координатах. Приложения двойных интегралов. Вычисление тройных интегралов в декартовых и цилиндрических координатах. Приложения тройного интеграла. Криволинейные интегралы I и II-го рода, вычисление, применение. Формула Грина. Независимость от пути интегрирования. Вычисление работы переменной силы. Поверхностные интегралы, их вычисление, приложения.
11 Числовые и функциональные ряды – 8ч. [1,2,5,6,7]
Исследование сходимости знакоположительных рядов. Знакопеременные ряды. Абсолютная и условная сходимость. Признак Лейбница. Область сходимости функционального ряда. Степенные ряды и их приложения. Ряды Фурье.
12 Теория вероятностей - 14ч. [3,4]
Основные формулы комбинаторики. Классическое определение теории вероятности. Геометрические вероятности. Условная вероятность. Теоремы сложения и умножения вероятностей. Формула полной вероятности. Формула Байеса. Схема Бернулли. Локальная и интегральная теоремы Муавра-Лапласса. Дискретные случайные величины. Законы распределения. Непрерывные случайные величины. Функция распределения, плотность распределения. Числовые характеристики. Биномиальное распределение, распределение Пуассона, равномерное и нормальное распределения.
График контроля
| Контрольное испытание | Время проведения | Весовой коэффициент | Примечания |
| ИДЗ-4 | 3 неделя | 0,05 | |
| КР по теме 10 | 4 неделя | 0,1 | 5 задач |
| ИДЗ-5 | 6 неделя | 0,05 | |
| ИДЗ-6 | 10 неделя | 0,05 | |
| КР по теме 11 | 11 неделя | 0,1 | 10 задач |
| ИДЗ-7 | 16 неделя | 0,05 | |
| КР по теме 12 | 17 неделя | 0,1 | 6 задач |
| Экзамен | сессия | 0,5 | 2 вопроса, 3 задачи. |