Напряженно-деформированное состояние круглого бруса

КРУЧЕНИЕ

Основные понятия

Крутящие моменты T в поперечных сечениях бруса обычно возникают под действием внешних моментов Т_e. Вращающийся стержень, подверженный преимущественно кручению, называется валом. Внешние моменты передаются на вал, как правило, в местах поса­дки на него шкивов, зубчатых колес и т.п. Если непосредственно вблизи от этих мест помещены опоры, то можно пренебречь сравнительно небольшим влиянием изгиба и рассчитывать вал только на кручение.

Рис. 9.1 Рис. 9.2

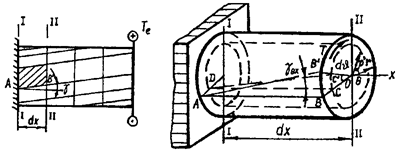
Для получения наглядного представления о деформации возь­мем резиновый круглый цилиндрический брус с нанесенной прямоу­гольной сеткой, составленной семейством концентрических окружнос­тей и образующими. Закрепим один конец и приложим к другому момент Т_e (рис.9.1). Полученная в результате деформирования сетка из параллелограммов свидетельствует о величине сдвига. Окружности остаются неизменными, и расстояния между ними не меняются. На основании гипотезы плоских и жестких сечений (см. п. 7.1) каждое поперечное сечение поворачивается в своей плос­кости на некоторый угол как жесткое целое. Радиусы всех сече­ний будут поворачиваться, оставаясь прямолинейными. Тем самым можно предположить, что характер деформаций, наблюдаемых на поверхности, будет таким же и внутри бруса на любой цилиндри­ческой поверхности, концентричной с наружной.

Для установления геометрических соотношений рассмотрим элемент бруса (см. рис. 9.1) между сечениями I-I и II-II (сечение I-I условно закреплено) и сконцентрируем внимание на линии АВ ′ и радиусе OВ ′, которые до деформации занимали положение АВ и OВ (рис. 9.2). Поворот образующей АВ связан с из-

менением положе­ния радиуса OB. Угол d 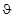называется углом закручивания.

Перемещение точки С на радиусе ОВ связано с поворотом образующей DC

цилиндра произвольного радиуса ρ. Сопоставим длину дуги СС′ из двух вычислений:

dx γ_{θ x} = ρ d ,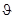

откуда

γ_{θ x} = (d 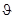/dx)ρ.

Относительный угол закручивания назовем кривизной круче­ния и обозначим k_t. Таким образом, имеем

k_t = d 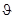/dx, γ_{θ x} = k_t ρ.

Напряженно-деформированное состояние круглого бруса

Для чистого кручения круглого цилиндрического бруса зада­ются следующие условия (используем цилиндрическую систему ко­ординат, см.рис.9.2): 1) в плоскости, касательной к цилин­дрической поверхности, имеет место чистый сдвиг (γ _{x θ}= const); 2) отсутствуют линейные деформации (ε _х = ε_ρ = ε_θ = 0), а следова­тельно, и нормальные напряжения и соответствующие им внутрен­ние усилия в поперечных сечениях бруса (продольная сила и из­гибающие моменты); 3) кривизна кручения в точках поперечного сечения сохраняет постоянное значение; 4) физический закон – закон Гука при сдвиге; 5) задан крутящий момент Т, Q_y = Q_x = 0. При заданных условиях по всей длине бруса соблюдается симмет­рия относительно оси х (осевая, круговая), заключающаяся в том, что при обходе в каждом сечении по дуге окружности угол сдвига γ _{x θ} не меняет величину и направление. Значит, в точке ρ = 0 имеем γ _{x θ} = 0, τ _{x θ} = 0.

Для определения характеристик скручиваемого бруса k_t, γ _{x θ,}τ _{x θ} и 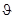привлекаем зависимости по трем законам деформиро­вания:

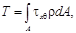
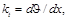
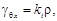
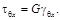
За основное неизвестное принимаем k_t. На основании двух последних зависимостей получаем τ_{θ x} = G γ_{θ x} = Gk_t ρ. По закону па­рности касательных напряжений τ _{х θ} = τ_{θ x} = Gk_t ρ. Подставим это значение в интегральную формулу

,

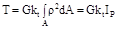откуда

k_t = T /(GI_Р).

Следовательно,

γ _{x θ}= (T ρ)/(GI_Р), τ_{х θ} = (T ρ)/ I_Р.

Наибольшее напряжение (на контуре сечения) равно

τ _{мах х Kt} = (Тr)/ I_Р = T/W_Р,

где W_Р - полярный момент сопротивления кругового сечения,

W_Р = (π r³)/2.

Дифференциальное уравнение углов закручивания имеет вид

d 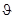/ dx = T /(GI_P).

Его интеграл

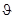= ∫[ T /(GI_P)] dx + С = (Tx)/(GI_P) + С.

Из условия: при х = 0, 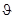= 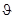(0) следует, что С = 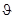(0), и сле­довательно,

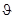= (Tx)/(GI_ρ) + 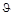(0).

Анализ полученного решения приводит к следующим выводам:

1. Кривизна кручения остается постоянной по длине бруса.

2. Напряжения τ _{х θ} не меняют своего закона по длине бруса и являются функцией только координаты ρ. На торцах на основании статического граничного условия они трансформируются в распределенную линейно вдоль радиусов нагрузку, которая и соответствует рассмотренной деформации.

3. Кривизна кручения и деформация сдвига пропорциональны величине GI_P, называемой жесткостью при кручении.