Построение разного рода оценок и статистических критериев часто основывается на использовании ряда специальных распределений случайных величин.
Нормальное распределение. Случайная величина  имеет нормальное распределение с параметрами
имеет нормальное распределение с параметрами  и
и  , что обозначается как
, что обозначается как  , если плотность вероятности этой случайной величины имеет вид
, если плотность вероятности этой случайной величины имеет вид
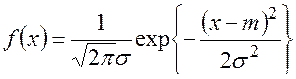 . (3.25)
. (3.25)
График плотности вероятности случайной величины, имеющей нормальное распределение, представлен на рисунке 3.5, на котором видно, что максимум функции находится в точке  .
.
Поскольку нормальное распределение подробно изучается в курсе теории вероятностей, напомним свойства нормальной случайной величины, которые будут использоваться в дальнейшем.
 |
Рис. 3.5
1)  ,
,  .
.
2) Случайная величина называется центрированной, если ее математическое ожидание равно нулю. Для того чтобы центрировать случайную величину, надо вычесть из нее математическое ожидание:
 .
.
3) Случайная величина называется нормированной, если ее дисперсия равна единице, а математическое ожидание равно нулю.
Для того чтобы нормировать случайную величину, надо ее поделить на среднее квадратическое отклонение:
 .
.
Центрированная и нормированная нормальная случайная величина называется стандартной. Таким образом, стандартной будет случайная величина
 ~
~  . (3.26)
. (3.26)
Вероятность попадания случайной величины  в интервал (α,β) вычисляется по формуле
в интервал (α,β) вычисляется по формуле
 , (3.27)
, (3.27)
где  - интеграл вероятности, представляющий собой функцию распределения стандартной нормально распределенной случайной величины. Интеграл вероятности табулирован. Его значения приведены в таблице В Приложения.
- интеграл вероятности, представляющий собой функцию распределения стандартной нормально распределенной случайной величины. Интеграл вероятности табулирован. Его значения приведены в таблице В Приложения.
Для стандартной нормальной случайной величины и симметричного промежутка формула (3.27) принимает следующий вид:
 . (3.28)
. (3.28)
Распределение  (хи-квадрат). Если
(хи-квадрат). Если  ,
,  независимые стандартные нормальные случайные величины, то говорят, что случайная величина
независимые стандартные нормальные случайные величины, то говорят, что случайная величина
 (3.29)
(3.29)
имеет распределение хи-квадрат с  степенями свободы, что обозначается как
степенями свободы, что обозначается как  . Графики плотности вероятности для двух значений степени свободы приведены на рис.3.6.
. Графики плотности вероятности для двух значений степени свободы приведены на рис.3.6.
 |
Рис. 3.6
С увеличением числа степеней свободы  плотность вероятности стремится к нормальной. При
плотность вероятности стремится к нормальной. При  плотность вероятности постоянно убывает, а при
плотность вероятности постоянно убывает, а при  имеет единственный максимум
имеет единственный максимум  ,
,  ,
,  .
.
Распределение Стьюдента. Пусть  ,
,  ,
,  ,
,  - независимые стандартные нормальные случайные величины. Тогда случайная величина
- независимые стандартные нормальные случайные величины. Тогда случайная величина
 (3.30)
(3.30)
имеет распределение Стьюдента с  степенями свободы, что обозначается как
степенями свободы, что обозначается как  , при этом
, при этом
 ,
,  .
.
На рис.3.7 приведены кривые стандартного нормального распределения (кривая 1) и плотности распределения Стьюдента (кривая 2).
 |
Рис. 3.7
При 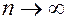 плотность распределения Стьюдента стремится к плотности стандартной нормальной случайной величины.
плотность распределения Стьюдента стремится к плотности стандартной нормальной случайной величины.
На практике, как правило, используется не плотность вероятности, а квантиль распределения. Напомним, что квантилью порядка (или уровня)  непрерывной случайной величины
непрерывной случайной величины  называется такое ее значение
называется такое ее значение  , которое удовлетворяет равенству
, которое удовлетворяет равенству 
 ,
,
где  - функция распределения, а
- функция распределения, а  - заданное значение вероятности. Рис.3.8 поясняет понятие квантили порядка
- заданное значение вероятности. Рис.3.8 поясняет понятие квантили порядка  .
.
 |
Рис. 3.8
Следующая теорема устанавливает свойства основных выборочных характеристик, вычисленных по выборке, соответствующих нормальному распределению.
Теорема Фишера. Пусть  - случайная выборка из генеральной совокупности
- случайная выборка из генеральной совокупности 
 , тогда выборочное среднее
, тогда выборочное среднее  и несмещенная выборочная дисперсия
и несмещенная выборочная дисперсия 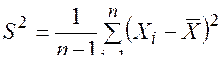 независимы, и при этом
независимы, и при этом
1) случайная величина  имеет распределение
имеет распределение  ;
;
2) случайная величина  имеет распределение
имеет распределение  ;
;
3) случайная величина  имеет распределение
имеет распределение 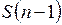 .
.
Доказательство теоремы приведено в [2].