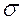h= 
= 
Вероятность попадания в интервал 
P 
Пример 5.8. Случайная величина распределена по нормальному закону с плотностью вероятности
f (x)= 
.
Найти её математическое ожидание, дисперсию, среднее квадратическое отклонение, вероятность попадания в интервал [-2;-1]. Построить кривую плотности вероятности этой случайной величины.
Решение
1. По виду формулы плотности вероятности определяем, что случайная величина распределена по нормальному закону, для которого плотность вероятности f (x) = 
. Приведем заданную функцию к стандартному виду:
f (x)= 
= 
.
Отсюда следует, что m = -1.5; σ = 0.5. Известно, что параметр m – математическое ожидание M [h], а σ - среднее квадратическое отклонение σ h. Следовательно, M [h] = -1.5, σ h=0.5, D [h] = 
=0.25.
2. Найдем вероятность попадания заданной случайной величины в интервал [-2,-1]. По свойствам функции распределения вероятность попадания случайной величины в интервал 
,
где F (x) – функция распределения случайной величины. Для нормально распределенной случайной величины функция распределения F (x) может быть выражена через её нормированную функцию Ф(х) формулой:
F (x)= Ф 
. (5.5)
Функция Ф(х) табулирована (см. табл. В приложения).
Таким образом
Р 
. (5.6)
Для решаемой задачи: 
s=0,5 т.е.
Учитывая, что Ф(- х)=1- Ф(х), и найдя в табл.В приложения Ф(1)=0.8413, получим
Р (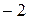
£h<-1)=2Ф(1)-1=0,6826.
3. Построим кривую плотности вероятности. Для этого на графике построим сначала кривую нормированной плотности вероятности (на рис. 5.6 штриховая линия 1), т.е.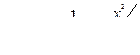 
. Затем сожмем её по оси ординат и растянем по оси абсцисс в σ раз (т.е. максимум увеличится в два раза). Получим пунктирную линию 2. И, наконец, сдвинем по оси абсцисс на величину m влево, т.е. в данном случае максимум графика будет в точке х =-1,5. Окончательный результат на рисунке изображен сплошной линией.
Рис. 5.6
Пример 5.9. Найти математическое ожидание и среднее квадратическое отклонение случайной величины, распределенной по нормальному закону,
если P { X >60}=0,98 и P { X <90}=0,84.
Решение. Для определения искомых числовых характеристик следует найти параметры распределения предлагаемой случайной величины, так как для нормально распределенной случайной величины математическое ожидание совпадает с параметром m, а среднее квадратическое отклонение с параметром σ. Для этого воспользуемся формулой, выражающей вероятность попадания случайной величины в данные в условиях интервалы через функцию распределения. Преобразуем задания в условии задачи равенства:
из P { x >60}= 0,98 получим р { х £60} = 1- р (х >60) = 1-0,98. Отсюда
P { x £60}=0,02.
По формуле (5.5) преобразуем левую часть, получим
F (60)= Ф(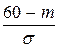
)= 0,02.
Теперь по таблицам Ф(х) (табл. В приложения) необходимо найти значение х, при котором Ф(х) равняется 0,02. Такого значения в таблице нет, это означает, что искомое значение – отрицательное. Используя формулу
Ф(- х)= 1-Ф(х), (5.7)
можно записать
Ф(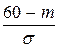)= 1-Ф(
)= 0,02,
т.е. Ф()= 0,98.
По табл.В приложения находим, что Ф(х)= 0,98 соответствует значению х =2,056, т.е. = 2,056.
Таким образом m -2.056 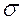=60.
Из второго условия следует P{X<90}=F(90)=Ф(
= 0,84; по табл. В Приложения находим аргумент для значения функции 0,84 и получаем 
=0,995, отсюда m +0,995 σ =90. Таким образом получаем систему уравнений относительно параметров 
и σ:
Находим из системы искомые параметры: 3,051 σ =30, σ @9,83, m =60+2,05×9,83 @ 80,15.
Итак, M [x ]=80,15, а σ =9,83 .