Предположим, что выполнено  измерений некоторой случайной величины ξ:
измерений некоторой случайной величины ξ: 
 ,...,
,...,  , (4.4)
, (4.4)
и есть основания полагать, что результаты распределены нормально с плотностью вероятности
 . (4.5)
. (4.5)
Параметры закона распределения  и σ обычно неизвестны. Вместо неизвестных параметров подставляют значения их оценок, которые вычисляют по следующим формулам:
и σ обычно неизвестны. Вместо неизвестных параметров подставляют значения их оценок, которые вычисляют по следующим формулам:
 , (4.6)
, (4.6)
 . (4.7)
. (4.7)
В качестве критерия проверки выдвинутой гипотезы примем критерий согласия Пирсона (критерий согласия “хи- квадрат”)
 , (4.8)
, (4.8)
где  – число интервалов, на которые разбито выборочное распределение,
– число интервалов, на которые разбито выборочное распределение, 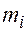 - частоты эмпирического распределения;
- частоты эмпирического распределения;  – частоты теоретического распределения. Из формулы вытекает, что критерий характеризует близость эмпирического и теоретического распределений: чем меньше различаются
– частоты теоретического распределения. Из формулы вытекает, что критерий характеризует близость эмпирического и теоретического распределений: чем меньше различаются 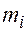 и
и  , тем меньше значение χ2.
, тем меньше значение χ2.
Доказано, что при  закон распределения случайной величины (4.8) независимо от того, какому закону распределения подчинена генеральная совокупность, стремится к закону распределения χ2 с
закон распределения случайной величины (4.8) независимо от того, какому закону распределения подчинена генеральная совокупность, стремится к закону распределения χ2 с 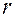 степенями свободы. Число степеней свободы определяется равенством
степенями свободы. Число степеней свободы определяется равенством 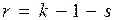 , где
, где  - число частичных интервалов;
- число частичных интервалов;  – число параметров предполагаемого распределения, которые были оценены. Для нормального распределения оцениваются два параметра (математическое ожидание и среднее квадратическое отклонение), поэтому
– число параметров предполагаемого распределения, которые были оценены. Для нормального распределения оцениваются два параметра (математическое ожидание и среднее квадратическое отклонение), поэтому  .
.
В соответствии с процедурой проверки гипотезы следует вычислить наблюдаемое значение критерия. Чтобы вычислить частоты эмпирического распределения, весь интервал наблюдаемых значений делят на  частичных интервалов (бинов) точками
частичных интервалов (бинов) точками 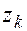 :
:
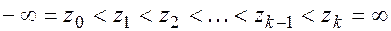 . (4.9)
. (4.9)
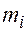 определяют, подсчитав число измерений (4.4), которые попадают в
определяют, подсчитав число измерений (4.4), которые попадают в  - й интервал
- й интервал  .
.
Используя теоретический закон распределения (4.5) можно рассчитать ожидаемое число  результатов измерений для каждого интервала
результатов измерений для каждого интервала  . Вероятность того, что результат одного измерения попадает в интервал
. Вероятность того, что результат одного измерения попадает в интервал  , равна
, равна
 , (4.10)
, (4.10)
где 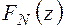 – интегральный закон нормального распределения:
– интегральный закон нормального распределения:  . Учитывая, что функция распределения
. Учитывая, что функция распределения  с параметрами
с параметрами  и σ связана со стандартной нормальной функцией формулой
и σ связана со стандартной нормальной функцией формулой  , соотношение (4.10) можно записать в следующем виде:
, соотношение (4.10) можно записать в следующем виде:
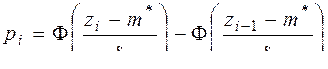 . (4.11)
. (4.11)
Поскольку проводится не одно, а  измерений и эти измерения независимы, то их можно рассматривать как
измерений и эти измерения независимы, то их можно рассматривать как  испытаний Бернулли, в которых “успехом” считается попадание результата измерения в интервал
испытаний Бернулли, в которых “успехом” считается попадание результата измерения в интервал  . Тогда числа
. Тогда числа  вычисляются по формуле
вычисляются по формуле
 (4.12)
(4.12)
(математическое ожидание числа “успехов” при  испытаниях).
испытаниях).
Для заданного уровня значимости по таблицам определяют критическое значение критерия. Сравнивая наблюдаемое и критическое значения критерия делают, вывод о соответствии экспериментальных данных предполагаемому закону распределения.
Пример 4.1. Проверить с помощью критерия χ2 при уровне значимости 0,05 гипотезу о том, что выборка объема 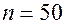 , представленная интервальным вариационным рядом в таблице 4.4, извлечена из нормальной генеральной совокупности.
, представленная интервальным вариационным рядом в таблице 4.4, извлечена из нормальной генеральной совокупности.
Таблица 4.4
| Номер интервала i | Границы интервала | Частота
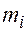
|
| 0 – 2 | ||
| 2 – 4 | ||
| 4 –6 | ||
| 6 – 8 | ||
| 8 – 10 |
Решение. 1. Сформулируем нулевую и альтернативную гипотезы: H0 – эмпирическое распределение соответствует нормальному; H1 - эмпирическое распределение не соответствует нормальному.
Для проверки нулевой гипотезы необходимо рассчитать наблюдаемое значение критерия χ2набл по формуле (4.8) и сравнить его с критическим значением χ2кр.
2. Определим параметры предполагаемого (теоретического) нормального закона распределения.
Найдем середины интервалов 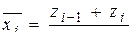 и относительные частоты
и относительные частоты  . Получим следующие значения:
. Получим следующие значения:

| |||||

| 
| 
| 
| 
| 
|
Оценку математического ожидания найдем по формуле (4.1):

 .
.
Оценки дисперсии и стандартного отклонения вычислим по формулам (4.2) и (4.3):

 ;
;
 .
.
3. Выполним расчет теоретических частот  по формуле (4.12). Для вычисления вероятностей
по формуле (4.12). Для вычисления вероятностей  по формуле (4.11) воспользуемся таблицей В Приложения со значениями нормальной стандартной функции распределения. При этом наименьшее значение, т. е.
по формуле (4.11) воспользуемся таблицей В Приложения со значениями нормальной стандартной функции распределения. При этом наименьшее значение, т. е.  , полагаем равным
, полагаем равным  , а наибольшее, т.е.
, а наибольшее, т.е.  , полагаем равным
, полагаем равным  . Последовательно находим для интервала (-∞, 2)
. Последовательно находим для интервала (-∞, 2)
 и
и 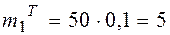 ;
;
для интервала  находим
находим

и  ;
;
для интервала (4,6) соответственно:

 ;
;
для интервала (6,8):

и  ;
;
для интервала  вычислим
вычислим
 ;
;
 .
.
4. По формуле (4.8) найдем значение  :
:

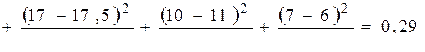 .
.
5. По таблице квантилей распределения χ2 (см. таблицу С Приложения) с числом степеней свободы 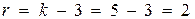 находим, что χ2кр = 6,0 для
находим, что χ2кр = 6,0 для  .
.
Поскольку 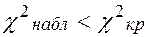 (
( ), то можно считать, что гипотеза о нормальном распределении генеральной совокупности не противоречит опытным данным.
), то можно считать, что гипотеза о нормальном распределении генеральной совокупности не противоречит опытным данным.