Наиболее типичный индекс этой группы – индекс объёма (индекс физического объёма), он может быть построен двумя способами: либо как агрегатный, либо как средний из индивидуальных индексов.
А) Агрегатный индекс физического объёма. Пусть известны данные о производстве различных видов продукции – А, Б и В – одного предприятия (или группы предприятий) за два периода:
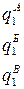
Необходимо при помощи общего индекса определить среднее изменение объёма выпуска всей продукции.
Простое суммирование (
) здесь невозможно (так как качественно разные виды продукции), поэтому требуется определённый соизмеритель. Таким соизмерителем могут служить себестоимость единицы продукции, затраты труда на производство единицы продукции и т.д., но чаще всего в этом качестве выступает цена единицы продукции. Умножая количество произведённой продукции на цену единицы продукции, получаем стоимостное выражение продукции каждого вида (величину товарооборота), которое уже допускает суммирование (qp). Стоимость продукции в базисном периоде будет равна:
, а в текущем периоде: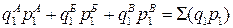 
.
Если сравнить эти два показателя, то получим изменение стоимости всей продукции (товарооборота) как за счёт цены единицы продукции, так и за счёт объёма продукции. В данном же случае поставлена задача определения изменения только объёма продукции, а цены пока остаются вне рассмотрения.
Поэтому, если объём продукции двух сравниваемых периодов оценить в одних и тех же ценах и сопоставить, то получим изменение стоимости всей продукции (товарооборота) только за счёт изменения объёма продукции. Это соотношение называется агрегатным индексом физического объёма и записывается следующим образом:
|
|
,
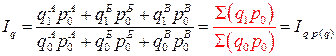где 
– цена единицы продукции в базисном периоде.
Данный индекс показывает, как в среднем изменился объём всей выпущенной (реализованной) продукции в текущем периоде по сравнению с базисным периодом
или как изменилась стоимость продукции (величина товарооборота) в текущем периоде по сравнению с базисным за счёт изменения объёма выпуска (реализации) продукции.
Разность между числителем и знаменателем агрегатного индекса характеризует в абсолютном выражении изменение стоимости продукции (величины товарооборота) за счёт изменения объёма выпуска (реализации) продукции:
.
Б) Средний арифметический и средний гармонический индексы физического объёма. Пусть по отдельным видам продукции рассчитаны индивидуальные индексы объёма (
), а затем из них требуется рассчитать средний индекс. Этот средний индекс может быть записан в форме средней арифметической или средней гармонической взвешенной:
,
где 
– индивидуальные индексы объёма; 
– веса соответственно в среднем арифметическом и среднем гармоническом индексах.
Для определения весов исходят из тождества этих индексов агрегатному, который является основной формой записи индексов. Следовательно, веса индексов должны определяться, исходя из следующих равенств:
.
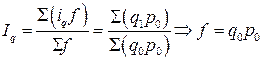Таким образом,
.
Аналогично и для среднего гармонического индекса:
.
Таким образом,
.
Для решения конкретных задач выбор той или иной формы среднего индекса определяется, прежде всего, наличием исходных данных.