Основные характеристики рядов динамики

1)Средний уровень ряда

а) для интервальных рядов с равными интервалами средний уровень ряда рассчитывается как средняя арифметическая простая из отдельных уровней:
, где – средний уровень ряда; – i -тый уровень ряда; n – число уровней ряда.

Пример:

б) для интервальных рядов с неравными интервалами средний уровень ряда определяется по формуле средней арифметической взвешенной:

, где t_i – период времени (число лет, месяцев и т.д.), в течение которого i -тый уровень ряда не изменялся.
Пример:

в) в моментных рядах динамики каждый уровень ряда условно можно рассматривать как показатель, относящийся одновременно к началу одного периода и концу другого периода:

I II III

1.01 1.02 1.03 1.04

(31.12) (31.01) (28.02) (31.03)

Рассчитаем средние уровни для каждого месяца:

Моментный ряд, таким образом, превращается в ряд интервальный; далее определяем средний уровень ряда как среднюю арифметическую простую:

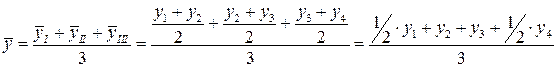
Таким образом, в общем случае получаем:

, где n – число уровней ряда.

Такая средняя называется средней хронологической для моментных рядов с равноотстоящими уровнями.

Пример:

г) в случае неравных промежутков времени между уровнями ряда (датами) среднюю рассчитывают как среднюю арифметическую взвешенную, приняв за веса отрезки времени между датами:

, где – средняя за i -тый промежуток времени; t_i – период времени, к которому относится эта средняя (число месяцев).

Пример:

Для расчёта остальных характеристик рядов динамики используют интервальные ряды с равными интервалами, как наиболее часто встречающиеся в экономической практике.

2)Абсолютный прирост рассчитывается как разность между двумя уровнями ряда:

– цепной абсолютный прирост ;

– базисный абсолютный прирост .

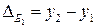
Сумма последовательных цепных приростов равна соответствующему базисному, т.е. общему абсолютному приросту за весь период:

– средний абсолютный прирост () рассчитывается как средняя арифметическая простая из цепных абсолютных приростов за отдельные последовательные периоды времени:

, где n – число уровней ряда.

3)Темп роста – относительный показатель, получающийся в результате деления двух уровней, измеряется в процентах или в коэффициентах:

– цепной темп роста (коэффициент) ;
– базисный темп роста (коэффициент) ;

– средний коэффициент (темп) роста исчисляется как средняя геометрическая:

, где – цепные коэффициенты роста; m – число цепных коэффициентов роста; .

В случае, когда имеются только уровни ряда, применяется другая формула:

. Используя указанную формулу, возможно рассчитать и прогнозные уровни ряда динамики. Если известен и исходный уровень ряда y₁, то при условии сохранения тенденций изменений в ряду динамики прогнозное значение можно определить следующим образом:

При расчёте средних темпов роста по периодам времени различной продолжительности пользуются средними геометрическими, взвешанными по продолжительности периодов:

, где t_i – период времени, в течение которого сохраняется данный коэффициент роста.

4)Темп прироста характеризует относительную величину прироста и определяется как процентное отношение абсолютного прироста к предыдущему или базисному уровню: