Общие индексы качественных показателей

Наиболее типичным индексом качественных показателей является индекс цен, он также может быть построен либо как агрегатный, либо как средний из индивидуальных индексов.

А) Агрегатный индекс цен. Пусть имеются данные о ценах за единицу продукции за два периода. Необходимо установить, как изменились цены в среднем на всю продукцию. Сами цены за единицу продукции непосредственно суммировать некорректно (можно, если предположить, что и в текущем, и в базисном периодах выпускалось только по одному виду продукции каждого вида, но объём продукции изменялся), но можно суммировать и сопоставлять стоимости продукции . Для выявления изменения только цен надо устранить влияние на результативный показатель – товарооборот – количества (объёма) продукции. Для этого в ценах текущего и базисного периодов необходимо оценить один и тот же объём продукции.

Агрегатный индекс цен записывается, таким образом, в следующем виде:

.

Данный индекс носит название «индекс Германа Пааше » (1874г., Германия). Этот индекс показывает, как в среднем изменились цены на всю продукцию в текущем периоде по сравнению с базисным или как изменилась стоимость продукции (объём товарооборота) в текущем периоде по сравнению с базисным за счёт изменения цен.

Вычитая из числителя индекса его знаменатель, можно определить влияние этого фактора на результативный показатель (товарооборот) и в абсолютном выражении:

.

Б) Средний арифметический и средний гармонический индексы цен. Эти индексы записываются аналогично индексам физического объёма:

 

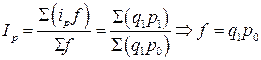
и

 

где – индивидуальные индексы цен.

 

 

При правильном построении индексов должна соблюдаться та же взаимосвязь, которая существует и между самими показателями. Если стоимость произведённой продукции (величину товарооборота) можно представить как произведение , то и произведение индекса физического объёма и индекса цен должно давать индекс стоимости продукции (товарооборота):

 

,

т.е. существует тождество, и индексы записаны правильно.

Существует взаимосвязь и на уровне абсолютных величин:

.

 

Таким образом, при записи индексов количественных и качественных показателей в дальнейшем следует исходить из того, что при изучении изменения качественного показателя количественный показатель нужно фиксировать на уровне текущего периода, а при изменении количественного показателя качественный показатель фиксируется на уровне базисного периода.

 

Исходя из взаимосвязанных факторов, можно записать индексы и для других сложных (результативных) показателей (справа – индексы качественных показателей, слева – индексы количественных показателей):

индекс затрат на производство продукции ;

индекс объёма продукции ;

индекс фонда заработной платы .

Индексы средних величин

 

Общей характеристикой качественного показателя служит его средняя величина, которая изменяется как под влиянием его значений у отдельных единиц совокупности, так и под влиянием весов этих отдельных единиц в совокупности (структуры).

В общем виде динамику таких средних показателей можно записать в виде соотношения:

,

которое называется индексом переменного состава.

Запись средних величин в индексах осуществляется с учётом взаимосвязи отдельных факторов; средняя величина должна иметь определённый экономический смысл, и, кроме того, удовлетворять формальным требованиям.

Индекс среднего уровня цен переменного состава записывается следующим образом:

.

Этот индекс показывает, как изменилась средняя цена за счёт изменения уровня цен на продукцию отдельных производителей (продавцов) и за счёт изменения объёма выпуска (продажи) продукции отдельными производителями (продавцами).

Чтобы исключить влияние изменения структуры совокупности на динамику средних величин, средние для двух периодов рассчитываются по одной и той же структуре. Такие средние называются стандартизированными, а их отношение носит название индекса фиксированного или постоянного состава.

Для цен это фиксирование одной и той же структуры находит отражение в следующей записи:

.

Этот индекс позволяет определить изменение средней цены за счёт изменения уровня цен отдельных производителей (продавцов). Зная индекс, можно найти и абсолютное значение этого влияния:

.

Индекс переменного состава отражает влияние двух факторов, индекс фиксированного состава – одного из этих двух факторов, и, следовательно, ещё один индекс будет отражать влияние другого фактора. Этот индекс называется индексом структурных сдвигов (структуры) и записывается следующим образом:

.

Данный индекс характеризует изменение средней цены за счёт изменения объёма выпуска (продажи) продукции отдельными производителями (продавцами). Можно определить и абсолютное влияние изучаемого фактора:

.

Вышеуказанные индексы взаимосвязаны:

.

Такая же связь существует и на уровне абсолютных величин:

.

Тема 4 «Ряды динамики»

Ряд динамики – это ряд числовых значений определённого статистического показателя в последовательные моменты или периоды времени. Числовые значения, составляющие динамический ряд, называются уровнями ряда.

В зависимости от показателей (уровней ряда) динамические ряды обычно подразделяются на ряды абсолютных, относительных и средних величин. Кроме того, уровни рядов динамики могут относится к определённым моментам (датам) или интервалам времени и в зависимости от этого различают моментные и интервальные ряды. Выделяют также ряды динамики с равноотстоящими и неравноотстоящими уровнями, равными и неравными интервалами.

Примеры динамических рядов:

Моментный ряд с равноотстоящими уровнями:

Товарная продукция, тыс. руб.
Дата	1.01	1.02	1.03	1.04	1.05	1.06	1.07

 

Моментный ряд с неравноотстоящими уровнями:

Товарная продукция, тыс. руб.
Дата	1.01	1.02	1.04	1.09	1.10	1.01

Интервальный ряд с равными интервалами:

Товарная продукция, млн. руб.
Год

Интервальный ряд с неравными интервалами:

Товарная продукция, млн. руб.
Годы	1993-94	1995-98	1999-2000

 

 

Прежде чем анализировать динамический ряд, надо убедиться в сопоставимости уровней ряда. Для приведения рядов динамики к сопоставимому виду используют приём, который называется «смыкание рядов динамики ». Под таким смыканием понимают объединение в один ряд двух или нескольких рядов динамики, уровни которых исчислены по разной методологии или разным территориальным границам. Для осуществления смыкания необходимо, чтобы для одного из периодов имелись данные, исчисленные по разным методологиям (или в разных границах). Находится соотношение таких уровней (по новой и старой методологиям), и на полученный коэффициент умножаются данные, которые пересчитываются (исчисленные по старой методологии).

Другой способ смыкания рядов динамики заключается в том, что уровень года, в котором произошли изменения, как до изменений, так и после изменений принимается за 100%, а остальные уровни пересчитываются в процентах по отношению к этому уровню соответственно.

ПРИМЕР:

Имеются следующие данные об объёме реализации продукции объединения автозаправочных станций, млн. руб.:

Объём реализации	2005г.	2006 г.	2007 г.	2008 г.	2009 г.	2010г.	2011 г.
Продукция 10 АЗС					-	-	-
Продукция 12 АЗС	-	-	-

 

Показатели за 2008-2011 гг. несопоставимы непосредственно с показателями за 2005-2007 гг., так как относятся к различному количеству АЗС. Задача состоит в исчислении данных за 2005-2007 гг. в новых границах (по новому числу АЗС), её решение осуществляется смыканием рядов. Для этого при расчётах по первому способу по данным 2008 г. исчисляется коэффициент соотношения уровней двух рядов: 168/140=1,2.

Умножая на этот коэффициент уровни первого ряда, получаем скорректированные данные за 2005-2007 гг. в новых границах, млн. руб.:

уровень 2005 г.- 120*1,2=144

уровень 2006г. - 125*1,2=150

уровень 2007 г. - 130*1,2=156

Смыкание рядов даёт возможность устранить несопоставимость уровней и получить представление о динамике за весь период. Однако при этом следует иметь в виду, что результаты, полученные путём смыкания рядов, являются приближёнными, т.е. содержат некоторую погрешность.

Расчёты по второму способу:

уровень 2005 г.: 120/140*100%=85,7% 168*85,7%/100%=144 млн.руб.

уровень 2006 г.: 125/140*100%=89,3% 168*89,3%/100%=150млн.руб.

уровень 2007 г.: 130/140*100%=92,9% 168*92,9%/100%=156млн.руб.

уровень 2008 г.: 100% 168 млн. руб.

уровень 2009 г.: 180/168*100%=107,1% 168*107,1%/100%=180 млн. руб.

уровень 2010 г.: 195/168*100%=116,1% 168*116,1%/100%=195млн. руб.

уровень 2011 г.: 215/168*100%=128% 168*128,0%/100%=215млн. руб.

В итоге вычислений получаем следующую таблицу:

 

Объём реализации	2005г.	2006 г.	2007 г.	2008 г.	2009 г.	2010г.	2011 г.
Продукция 10 АЗС					-	-	-
Продукция 12 АЗС	-	-	-
Сопоставимый ряд 1
Сопоставимый ряд 2	(85,7%)	(89,3%)	(92,9%)	(100%)	(107,1%)	(116,1%)	(128,0%)