Эластичность спроса и предложения

РЕФЕРАТ

По теме «Использование производных и дифференциалов
в экономических исследованиях»

 

Выполнила студентка
Брестского государственного университета
имени А. С. Пушкина

специальности бизнес-администрирование

группы БА-11

Елец Александра Сергеевна

 

 

Июнь 2014

СОДЕРЖАНИЕ

ВВЕДЕНИЕ.........................................................................................................................3

ИСПОЛЬЗОВАНИЕ ПРОИЗВОДНЫХ В ЭКОНОМИЧЕСКИХ ИССЛЕДОВАНИЯХ.........................................................................................................4

Предельные величины....................................................................................4

Эластичность спроса и предложения.............................................................5

Прочие случаи..................................................................................................6

Пример задачи с использованием производной..........................................6

ИСПОЛЬЗОВАНИЕ ДИФФЕРЕНЦИАЛОВ В ЭКОНОМИЧЕСКИХ ИССЛЕДОВАНИЯХ.........................................................................................................7

Задачи с применением дифференциалов...............................................................7

Эффект финансового рычага.................................................................................7

ЗАКЛЮЧЕНИЕ........................................................................................................9

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ............................................10

ВВЕДЕНИЕ

Неразрывная связь между экономикой и математикой давно стала очевидна человечеству, ведь ведение хозяйства подразумевает множество математических вычислений. Ф.Энгельс в своё время заметил, что «лишь дифференциальное исчисление даёт естествознанию возможность изображать математически не только состояния, но и процессы: движение». Основа любой экономики – это производство, т.к. оно, производя продукцию, позволяет людям удовлетворять свои многочисленные потребности. Экономистам все время приходится решать одну глобальную задачу – как можно больше произвести, и при этом, как можно меньше затратить ограниченных ресурсов.

Дифференциальное исчисление – широко применяемый для экономического анализа математический аппарат. Базовой задачей экономического анализа является изучение связей экономических величин, записанных в виде функций. В каком направлении изменится доход государства при увеличении налогов или при введении импортных пошлин? Увеличится или уменьшится выручка фирмы при повышении цены на ее продукцию? В какой пропорции дополнительное оборудование может заменить выбывающих работников? Для решения подобных задач должны быть построены функции связи входящих в них переменных, которые затем изучаются с помощью методов дифференциального исчисления.

В данной работе приведены примеры использования производных и дифференциалов в экономических исследованиях.

 

1. ИСПОЛЬЗОВАНИЕ ПРОИЗВОДНЫХ В
ЭКОНОМИЧЕСКИХ ИССЛЕДОВАНИЯХ

Предельные величины

В экономической теории активно используется понятие «маржинальный», что означает «предельный». Введение этого понятия в научный оборот в XIX веке позволило создать совершенно новый инструмент исследования и описания экономических явлений – инструмент, посредством которого стало возможно ставить и решать новый класс научных проблем.

Предельные или пограничные величины характеризуют не состояние (как суммарная или средняя величины.), а процесс, изменение экономического объекта. Следовательно, производная выступает как интенсивность изменения некоторого экономического объекта (процесса) по времени или относительно другого исследуемого фактора.

Надо заметить, что экономика не всегда позволяет использовать предельные величины в силу прерывности (дискретности) экономических показателей во времени (например, годовых, квартальных, месячных и т.д.). В то же время во многих случаях можно отвлечься от дискретности и эффективно использовать предельные величины.

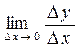Рассмотрим ситуацию: пусть y – издержки производства, а х – количество продукции, тогда Dx- прирост продукции, а Dy – приращение издержек производства.

В этом случае производная выражает предельные издержки производства и характеризует приближенно дополнительные затраты на производство дополнительной единицы продукции,, где MC –

предельные издержки (marginal costs); TC – общие издержки (total costs); Q – количество.

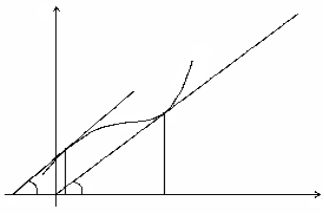
Геометрическая интерпретация предельных издержек – это тангенс угла наклона касательной к кривой в данной точке (см. рис.).

Аналогичным образом могут быть определены и многие другие экономические величины, имеющие предельный характер.

рис. 1

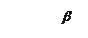
Другой пример – категория предельной выручки (MR— marginal revenue) — это дополнительный доход,

полученный при переходе от производства n-ной к (n+1)-ой единице продукта.

 

Она представляет собой первую производную от выручки:

При этом R= PQ, где R–выручка (revenue); P–цена (price).

Таким образом, Þ MR= P.

Это равенство верно относительно условий совершенной конкуренции, когда экономические агенты каждый по отдельности не могут оказать влияния на цену.

Еще одним примером использования производной в экономике является анализ производственной функции. Поскольку ограниченность ресурсов принципиально не устранима, то решающее значение приобретает отдача от факторов производства. Здесь также применима производная, как инструмент исследования. Пусть применяемый капитал постоянен, а затраты труда увеличиваются. Можно ввести в экономический анализ следующую категорию – предельный продукт труда MP_L(marginal product of labor) – это дополнительный продукт, полученный в результате дополнительных вложений труда (L – labor) при неизменной величине капитала:

Если вложения осуществляются достаточно малыми порциями, то

т.к. Dy – результат, Dl – затраты, то MP_L – предельная производительность труда.

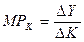Аналогично, MP_k – предельный продукт капитала – дополнительный продукт, полученный в результате дополнительных вложений капитала K при неизменной величине труда:

Если вложения осуществляются малыми порциями, то

MP_k – характеризует предельную производительность капитала.

Эластичность спроса и предложения

Для исследования экономических процессов часто используется понятие эластичности функции.

Понятие эластичности было введено Аланом Маршаллом в связи с анализом функции спроса. По существу, это понятие является чисто математическим.

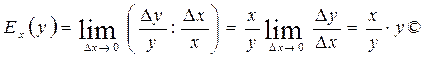Эластичностью функции Еx(y) называется предел отношения относительного приращения функции y к относительному приращению переменной x при Dx®0:

 

Эластичность функции показывает приближенно, на сколько процентов изменится функция y= f(x), при изменении независимой переменной x на 1%.

Приведем несколько конкретных иллюстраций такой зависимости. Прямой коэффициент эластичности спроса по цене устанавливает, на сколько процентов увеличивается (уменьшается) спрос Q на товар i при уменьшении (увеличении) его цены P на 1%:

Перекрестный коэффициент эластичности спроса по цене показывает, на сколько процентов изменится спрос на товар i при однопроцентных колебаниях цены товара j (j = 1,2,…n):.

Количественную сторону взаимодействия дохода и спроса отражает коэффициент эластичности спроса по доходу, который указывает, на сколько процентов изменится спрос на i -тый товар Q_i если доход, предназначенный на текущее потребление, изменится на 1%:.

В экономике очень часто требуется найти наилучшее или оптимальное значение показателя: наивысшую производительность труда, максимальную прибыль, максимальный выпуск, минимальные издержки и т. д. Каждый показатель представляет собой функцию от одного или нескольких аргументов. Таким образом, нахождение оптимального значения показателя сводится к нахождению экстремума функции.

Прочие случаи

В экономике очень часто требуется найти наилучшее или оптимальное значение показателя: наивысшую производительность труда, максимальную прибыль, максимальный выпуск, минимальные издержки и т. д. Каждый показатель представляет собой функцию от одного или нескольких аргументов. Таким образом, нахождение оптимального значения показателя сводится к нахождению экстремума функции.

Также известно, что производительность труда есть производная объема продукции по времени.

Пусть функция u = u(t) выражает количество произведенной продукции u за время t. Необходимо найти производительность труда в момент tο.

За период времени от tο до tο + Δt количество произведенной продукции изменится от значения uο = u(tο) до значения uο + Δu = u(tο + Δt). Тогда средняя производительность труда за этот период времени Zср = Δu:Δt. Очевидно, что производительность труда в момент tο можно определить как предельное значение средней производительности за период времени от tο до tο + Δt при Δt → 0, т.е.

z = lim Zср = lim Δu/Δt = u'(t) при Δt→0.

В процессе экономических исследований решаются различные задачи, многие из которых требуют применения использования производных и дифференциалов.