Задачу ЛП можно решать аналитическими и графическими методами. Аналитические методы являются основой для решения задачи на ЭВМ. Их единственный недостаток заключается в том, что в отличие от графических методов они недостаточно наглядны. Графические методы достаточно наглядны, но они пригодны лишь для решения задач на плоскости.
Теорема Вейерштрасса:
Непрерывная функция определяется на замкнутой области допустимых решений (ОДР) и достигает своих экстремальных значений либо внутри ОДР (в стационарных точках, в которых все частные производные обращаются в нуль), либо на ее границе.
Для линейной функции: 
 .
.
Поэтому линейная функция достигает своих экстремальных (максимальных, минимальных) значений на границе ОДР, как правило, в вершинах ОДР.
Алгоритм метода:
1) Построить систему ограничений в виде прямых.
2) Определить допустимую область, в которой ограничение выполняется. Для этого координаты произвольной точки подставляем в ограничение. Если неравенство выполняется, значит выбранная точка лежит в допустимой полуплоскости. Недопустимую полуплоскость будет зачеркивать
3) Определить область допустимых решений (ОДР), в которой выполняются все ограничения одновременно.
4) Рассчитать координаты вершин ОДР, из решения систем 2-х линейных уравнений, образующих эту вершину.
5) Вычислить значение критерия в каждой вершине. Из сопоставления полученных значений определить оптимальную вершину.
Пример 2. 3.1.
Трикотажное ателье изготавливает два вида изделий из шерстяной пряжи. Трудоемкость изготовления изделия вида A1 в 2,5 раза выше трудоемкости изготовления изделия вида А2. Если бы ателье выпускало только изделия вида А1, суточный объем производства мог бы составлять 26 изделий. Суточный объем сбыта изделий вида А1 ограничен до 17 изделий: изделий вида А2 – до 35 штук. Прибыль от продажи изделия вида А1 равна 20 дол., а изделия вида А2 – 11 долл. Определить, какое количество изделий каждого вида следует изготовлять ателье, чтобы получить максимальную прибыль.
Математическая формулировка задачи
х1 – количество изделий вида А1, х2 – количество изделий вида А2.
Получим ограничения на совместный выпуск продукции.
Так как трудоемкость изготовления изделий вида А2 в 2,5 раза ниже, то если бы ателье изготавливало только изделия вида А2, то ателье выпустило бы в 2,5 раза больше изделий, а именно 65 изделий вида А2 (2,5×26= 65).
Уравнение прямой, проходящей через точки К(26;0) и М(0;65)
 ;
;  ;
;
65×х1-26×65=-26×х2
65×х1+26× х2=1960 /13
5×х1+2×х2=130
тогда ограничение на совместный выпуск изделий примет вид
5×х1+2×х2  130
130
Математическая модель задачи
f=20х1+11х2®max
 х1£17 (1)
х1£17 (1)
х2£35 (2)
5×х1+2×х2  130 (3)
130 (3)
хi³0, i=1,2
Находим отрезки, которые прямая 5×х1+2×х2=130 (3) отсекает по осям:
при х1=0 5×0+2х2 =130; х2=  =65
=65
при х2=0 5×х1+2×0 =130; х1=  =26
=26


Рис.6. Графическое решение задачи
Допустимую область, в которой выполняется неравенство находим путем подстановки координат любой точки, например точки О(0;0) в неравенство. Если неравенство выполняется для точки, то эта точка принадлежит допустимой области. 5.0+2.0=0<130. Допустимая область лежит на прямой (3) и ниже. Зачеркиваем недопустимую область решений.
Переменная х1 ³ 0 в первом и четвертом квадранте, поэтому зачеркиваем второй и третий квадрант.
Переменная х2 ³ 0 в первом и втором квадранте, зачеркиваем недопустимые третий и четвертый квадранты.
Область допустимых решений - это многоугольник ОАВСД.
Найдем координаты вершины В из решения системы уравнений прямых (2) и (3).
 х2=35 (2)
х2=35 (2)
5×х1+2×х2=130 (3)
х1= 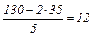
 Найдем координаты вершины С из решения системы уравнений прямых (1) и (3)
Найдем координаты вершины С из решения системы уравнений прямых (1) и (3)
х1=17 (1)
5×х1+2×х2=130 (3)
х1= 
Координаты каждой точки ОДР представляют допустимое решение этой задачи.
Рассчитаем координаты вершин:
(Ÿ)О (0;0) f(О)=0
(Ÿ)А (0;35) f(А)=20×0+11×35=385
(Ÿ)В (12;35) f(В)=20×12+11×35=625  max f
max f
(Ÿ)С (17;22,5) f(С)=20×17+22,5×35=587,5
(Ÿ)Д(17;0) f(D)=20×х1+11×х2=20×17+11×0=340
Оптимальная точка В, тогда оптимальный план выпуска изделий
Х* (12;35)