Анализ моделей на чувствительность - это процесс, реализуемый после того, как оптимальное решение задачи получено. В рамках такого анализа выявляется чувствительность оптимального решения к определенным изменениям исходной модели. При таком анализе всегда рассматривается некоторая совокупность линейных оптимизационных моделей, то есть по существу, некоторая модель исследования операций. Это придает модели определенную динамичность, позволяющую исследователю проанализировать влияние возможных изменений исходных условий на полученное ранее оптимальное решение.
Для проведения анализа будем использовать графический метод.
Пример 2.7.1.
Небольшая фабрика одной из фирм изготавливает два вида красок: для внутренних (I) и для наружных (E) работ. Продукция обоих видов поступает в оптовую продажу. Для производства красок используются два исходных продукта A и B. Максимально возможные суточные запасы этих продуктов составляют 6 т и 8 т соответственно. Расходы продуктов A и B на 1 т соответствующих красок приведены в таблице:
Таблица11
| Исходный Продукт | Расход исходного продукта на 1т краски | Мах ресурс | |
| Краска Е | Краска I | ||
| А | |||
| В | |||
| Оптовая цена 1 тонны краски, тыс. $ |
Изучение рынка сбыта показало, что суточный спрос на краску I никогда не превышает спроса на краску E более чем на 1 т. Кроме того, установлено, что спрос на краску I никогда не превышает 2 т в сутки.
Какое количество краски вида E и I должна производить фабрика, чтобы доход от реализации продукции был максимальным?
Обозначим: хE - суточный объем производства краски E (т).
хI - суточный объем производства краски I (т).
При допущении независимости объемов сбыта каждой из красок общий доход f0 равен сумме двух слагаемых 3хE + 2хI.
В целом математическая модель
f0=3хE+2хI® max
 при ограничениях: хE+2хI£ 6 (1)- на расход продукта А
при ограничениях: хE+2хI£ 6 (1)- на расход продукта А
2хE+хI£ 8 (2)- на расход продукта В
хI -хE£ 1 (3)- соотношение спросов на краски
хI £ 2 (4)- спрос на краску I
хI³ 0; хE³ 0
Данная математическая модель является линейной, так как целевая функция f0 и все ограничения линейны. Линейность предполагает наличие двух свойств - пропорциональности и аддитивности.
Пропорциональность ‑ означает, что вклад каждой переменной хI и хE в целевую функцию f0 и общий объем потребления соответствующих ресурсов прямо пропорционален уровню (величине) этой переменной.
Если, например, фирма будет предоставлять потребителям скидку, продавая краску E по 2, 5 тыс. долларов за тонну при объеме закупок свыше 2 тонн, то в этом случае прямой пропорциональности между доходом фирмы и величиной хE нет.
 |
Рис. 15.
Аддитивность - заключается в том, что каждая целевая функция представляет собой сумму вкладов от различных переменных. Аналогично левая часть каждого ограничения должна представлять собой сумму расходов, каждое слагаемое будет пропорционально величине соответствующей переменной.
Если, например, фирма производит два конкурирующих вида продукции, увеличение сбыта одного из которых отрицательно сказывается на объеме реализации другого, то такая модель не обладает свойством аддитивности.
На рис.15 данная задача решена графическим методом. Максимальное значение прибыли достигается в вершине D при плане выпуска:
хЕ = 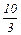 (т) и хI =
(т) и хI = 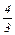 (т),
(т),
max f = 12 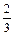 тыс.$
тыс.$
Первая задача анализа на чувствительность
Позволяет определить статус ресурсов и допустимые пределы изменения ресурсов.
Классифицируем ограничения линейной модели как связывающие (активные) и не связывающие (неактивные) ограничения. Прямая, представляющая активное ограничение, должна проходить через оптимальную вершину.
Вернемся к рассмотренному примеру о фирме, выпускающей краски Е и I. В нашем примере связывающие ограничения (1) и (2), они лимитируют запасы исходных продуктов (ресурсов) А и В.
Если ограничение является связывающим, то логично отнести соответствующий ресурс к разряду дефицитных ресурсов, так как он используется полностью. Ресурс, с которым ассоциировано несвязывающее ограничение, следует отнести к разряду не дефицитных ресурсов, потому что часть этого ресурса остается неиспользованной.
При анализе модели на чувствительность по правым частям ограничений определяют:
1) предельно допустимое увеличение запаса дефицитного ресурса, позволяющее улучшить найденное оптимальное решение max f0;
2) предельно допустимое снижение запаса недефицитного ресурса, не изменяющее max f0.
Информация по пункту 2 может быть полезна в тех случаях, когда излишки не дефицитных ресурсов могут быть использованы для других целей.
Может возникнуть вопрос: не следует ли проанализировать, как повлияет на оптимум:
1. увеличение объема ресурсов, имеющихся в избытке.
2. сокращение объема дефицитных ресурсов.
Ответ на первый пункт очевиден, т.е. в этом случае мы сделаем избыточный ресурс еще более избыточным, что никак не повлияет на полученное ранее решение. По второму пункту покажем, что сокращение дефицитного ресурса никогда не улучшает значение целевой функции.
На рис. 16 нарисуем ограничение хE+2хI £ 4. В этом случае оптимальной является (1¢) вершина N, координаты вершины определяют из совместного решения:
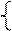 хE+2хI = 4 хE=4‑2хI хЕ(N)=4
хE+2хI = 4 хE=4‑2хI хЕ(N)=4
2хE+хI = 8 8- 4хI+хI=8 хI(N)= 0 f0(N)=12,
то есть оптимальное значение целевой функции уменьшилось с уменьшением запаса дефицитного ресурса (продукта А).
Рассмотрим теперь увеличение ресурса А, при этом прямая (1) (или отрезок СД) переместится вверх параллельно самой себе. Имеет смысл увеличить запас продукта так, чтобы прямая (1) прошла через вершину К. Большее увеличение продукта А приведет к тому, что ресурс (1) станет избыточным. В точке К ограничения (2) и (4) становятся связывающими. Оптимальное решение при этом достигается в вершине К, а ОДР становится многоугольник ОАВКЕ. Координаты вершины К:
 2×хE+хI=8 (2)
2×хE+хI=8 (2)
хI=2 (4)
хE=  =3 Þ К(3;2)
=3 Þ К(3;2)
f0(К)= 3×хE+2×хI = 3×3+2×2= 9+4 =13.
Для определения предельного запаса ресурса А следует координаты вершины К подставить в левую часть ограничения (1). Тогда новое значение запаса продукта А равно: хE+2×хI=3+2×2=7, т.е. следует увеличить запас продукта А на D1=7-6=1 (т), где 6 – это старое значение запаса продукта А.
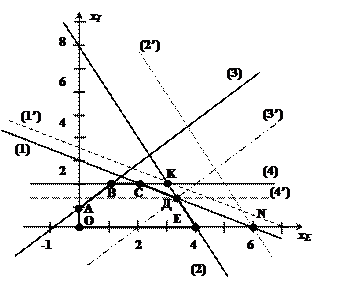 |
Рис. 16.
Рассмотрим вопрос о целесообразности увеличения запаса дефицитного ресурса (2) (исходный продукт В). Запас продукта В следует увеличить так, чтобы прямая (2) прошла через вершину N.
Новой оптимальной вершиной становится точка N, где пересекаются прямая (1) и ось абсцисс (хI=0) тогда
 хE+2хI=6
хE+2хI=6
хI=0
хE=6
f(N)=f(6;0)=18
Для нахождения величины запаса продукта В, который гарантирует прибыль f=18 тыс.$, подставим координаты вершины N в ограничение (2):
2хE(N)+ хI(N)=2×6=12.
Тогда абсолютный прирост запаса продукта В: D 2=12-8=4 (т)
Рассмотрим теперь вопрос об уменьшении правой части несвязывающих ограничений. Ограничение (4) (отрезок ВС) опускаем вниз до пересечения с оптимальной вершиной Д, так как координаты точки Д:
хE(Д)=3 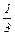 ; хI(Д)=1
; хI(Д)=1 
то уменьшение спроса на краску I до величины хI(Д)= 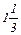 никак не повлияет на оптимальность ранее полученного решения.
никак не повлияет на оптимальность ранее полученного решения.
Сокращение спроса:
D 4= 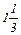 – 2 =
– 2 = 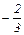
(знак ¢-¢ свидетельствует об уменьшении запаса ресурса).
Сокращение спроса адекватно уменьшению представительства на рынке, посредством которого реализуется краска вида I.
Рассмотрим ограничение (3), хE+хI£ 1, которое представляет соотношение между спросом на краску I и спросом на краску Е. И в этом случае правую часть ограничений можно уменьшать до тех пор, пока прямая (3) (отрезок АВ) не пройдет через оптимальную вершину Д. При этом правая часть ограничения (3) в точке Д станет равной:
хЕ (Д) +х I (Д) = 3 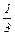 +1
+1 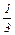 = -2
= -2
Сокращение запаса ограничения (3) D3=-2-1=-3
Вторая задача анализа на чувствительность
При ограничениях на затраты, связанные с дополнительным привлечением ресурсов (что характерно для большинства экономических задач), естественно задать вопрос: какому из ресурсов следует отдать предпочтение при вложении дополнительных средств?
Введем характеристику ценности yi дополнительной единицы дефицитного ресурса I. Величина ценности дополнительной единицы ресурса I, определяется из соотношения
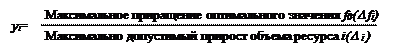 |
Воспользуемся таблицей
Таблица12
| Ресурс | Тип ресурса | Маx изменение ресурса, т (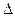 i) i)
| Маx изменение дохода от реализации тыс$ ( fi) fi)
| Ценность дополнительной единицы yi |
| А | дефицитный | 7 - 6 = + 1 | 13 -12 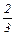 = + = + 
| 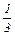
|
| В | дефицитный | 12 – 8 = + 4 | 18 - 12  =5 =5 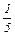
| 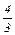
|
| соотношение спросов | недефицитный | - 2 –1= -3 | 12  - 12 - 12 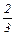 =0 =0
| 0 |
| Спрос на краску I | недефицитный | 1  - 2 = -3 - 2 = -3
| 12  - 12 - 12  =0 =0
| 0 |
Полученные результаты свидетельствуют, что дополнительные вложения в первую очередь следует направить на увеличение запаса продукта В, а лишь за тем на увеличение продукта А(y В> y A), что касается не дефицитных ресурсов, то их объем увеличивать не следует.
Третья задача анализа на чувствительность
В каких пределах допустимо изменение коэффициентов целевой функции?
f0= 3×хE+2×хI=CE×хE+CIхI
Изменение коэффициентов целевой функции оказывает влияние на наклон линии уровня. Какая вершина будет оптимальна, зависит, прежде всего, от наклона линии уровня, которая для линейной модели так же представляет собой прямую. Это означает, что вариация (изменение) коэффициентов целевой функции может привести к изменению совокупности связывающих ограничений, и следовательно статуса того или иного ресурса (т.е. сделать ресурс дефицитным и наоборот).
В рамках анализа модели на чувствительность к изменениям коэффициентов можно исследовать следующие вопросы:
1) каков диапазон изменения (увеличения или уменьшения) того или иного коэффициента целевой функции, при которых не происходит изменение оптимального решения?
2) на сколько можно изменить тот или иной коэффициент целевой функции, чтобы сделать не дефицитный ресурс дефицитным, и наоборот.
Построим линию уровня f = СЕ хЕ + СI xI = СE.СI
при хЕ = 0 хI = СE
при хI = 0 xE = СI
В исходной задаче СЕ =3; СI =2.
Из рис.17 видно, что при увеличении СЕ или уменьшении СI линия уровня f0 =const вращается вокруг точки Д по часовой стрелке.
Если СЕ уменьшается или СI увеличивается, то линия уровня вращается вокруг точки Д против часовой стрелки. Точка Д будет оптимальной до тех пор, пока наклон прямой не выйдет за пределы, определяемые наклонами прямых ограничений (1) и (2). Когда наклон линии уровня станет равным наклону прямой СД для ограничения (1), то получим две альтернативные угловые точки С и Д.
Аналогично, если наклон линии уровня равен наклону прямой ДЕ для ограничения (2) получим два альтернативных решения в вершинах Д и Е. Как только наклон линии уровня выйдет за пределы углов наклона прямых (1) и (2) получим новое оптимальное решение.
Как можно найти допустимый интервал изменения СЕ, при котором точка Д останется оптимальной? Будем полагать СI =2 неизменным.
Представим уравнение линии уровня f0=CEхE+2хI=const в форме прямой с угловым коэффициентом y=кх+b, где к=tga
хI=  .
.
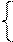 Запишем активные ограничения в форме прямой с угловым коэффициентом: хI=
Запишем активные ограничения в форме прямой с угловым коэффициентом: хI=  -
- 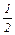 хE (1)
хE (1)
хI=8- 2хE (2)
|
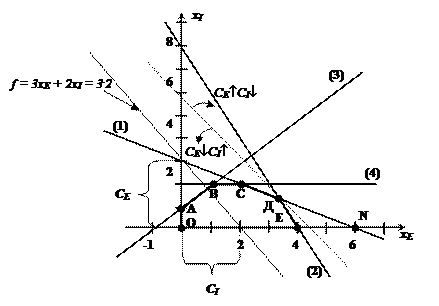
Рис. 17.
Тогда интервал изменения СЕ, при котором вершина Д по-прежнему остается оптимальной точкой и определяется неравенством
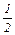 <
< 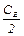 <2,
<2,
1< СЕ <4
4 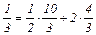 < f <
< f < 
При CЕ=1 оптимальными вершинами будут C и Д. Как только CЕ<1 оптимум смещается в точку С и ресурс (2) становится недефицитным, а (4) дефицитным. При CЕ=4 оптимальны две вершины Е и Д, при CЕ>4, оптимум смещается в точку Е.
Можно заметить, что как только коэффициент СE станет меньше 1, ресурс (2) становится недефицитным и для фирмы это означает, что если доход от продажи одной тонны краски Е станет меньше 1 тыс. дол., то наиболее выгодная производственная программа должна предусматривать выпуск максимально допустимого количества краски I (т.е. xI=2 тонны в сутки). Если значение СЕ > 4, то следует выпускать только краску Е, т.е. хЕ = 4, хI = 0.
Определим область изменения коэффициента СI для которой вершина Д по-прежнему будет оставаться единственной оптимальной вершиной. Исходное значение СЕ =3= const
f0=3xE+СIxI = const,
тогда хI =  ,
,
сравнивая угловые коэффициенты активных прямых получим:
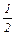 <
<  < 2
< 2
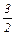 < СI < 6
< СI < 6
12 =  f
f 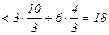
Пример: 2. 7. 2,
Университет не принимает более 4000 студентов своей страны, но разрешает прием любого количества иностранных студентов. Персонал университета составляет 440 преподавателей. Для обучения 12 студентов своей страны и 10 иностранных студентов требуется один преподаватель.
Необходимо, чтобы 40% студентов данной страны и 80% иностранных студентов могли разместиться в аудиториях, где имеется 2800 мест. Университет получает 2000 долл. в год из правительственных средств на каждого студента своей страны и берет плату в размере 3000 долл. в год за каждого иностранного студента. Из учета максимального дохода определите, какой прием студентов своей страны и иностранных студентов следует планировать. Произвести анализ задачи на чувствительность.
Обозначим х1 – количество студентов своей студентов своей страны;
х2 – число иностранных студентов.
Математическая модель
f=2000x1+3000x2® max
 х1£ 4000 (1)
х1£ 4000 (1)
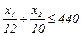 (2)
(2)
0,4х1+0,8х2£ 2800 (3)
хi³ 0 i=1,2

Рис.18
Прямая (2) пройдет через точки (0;4400) и (5280;0). Прямая (3) пройдет через точки (7000;0) и (0;3500).
Построим линию уровня целевой функции:
f =2000×x1+3000×x2=6000000
она пройдет через точки (3000;0) и (0;2000).
Максимум дохода достигается в вершине В. Найдем координаты вершины В из совместного решения уравнений (2) и (3).

 ,
,
0,4×х1+0,8×х2=2800 Þ х1=7000-2 х2.
Подставим х1 в уравнение (2)


или
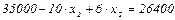
4х2 = 8600 Þ х2=2150
х1 = 2700
max f (2700; 2150)=11850 тыс. долл.
Произведем анализ на чувствительность графическим методом.
Дефицитными будут ресурсы (2) (количество преподавателей) и (3) (число мест в аудиториях), так как уравнения этих ограничений образуют оптимальную вершину. Недефицитным ресурсом является ограничение 1 (спрос на студентов своей страны).
Можно сократить недефицитный ресурс на величину избытка D1=2700 - 4000=-1300 (чел.), что никак не скажется на величине целевой функции.
Ресурс (2) мы можем увеличить на такую величину D2, чтобы прямая (2) прошла через точку N.
 Найдем координаты вершины N:
Найдем координаты вершины N:
Þ х2 = 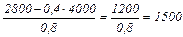
Точка N имеет следующие координаты: N(4000;1500)
f (N)=2000×4000+3000×1500=12500 тыс. долл.
Df2 =12500000-11850000=650000
Найдем новое значение ресурса (2), подставив координаты вершины N в левую часть ограничения (2).
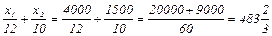
т.е. следует увеличить число преподавателей на величину:
D2=483 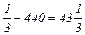
Ограничение (3) следует увеличить на такую величину, чтобы прямая (3) прошла через вершину М. Координаты точки М (0;4400).
Найдем новое значение ресурса (3)
0,4×х1+0,8×х2=0,4×0+0,8×4400=3520
D3=3520-2800=720
т.е. количество мест в аудиториях и лабораториях следует увеличить на 720 мест.
f (M)=2000×0+3000×4400=13200 тыс. долл.
Df2 =13200000-11850000=1350000
Таблица13
| Характеристика ресурса | Статус | Прирост i-го ресурса Di | Прирост дохода за счет изменения i-го ресурса D fi | Ценность ресурса уi= 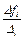
|
| Спрос на студен-тов своей страны | недефицит. | -1300 | 0 | 0 |
| Число преподавателей | дефицит. | 43 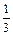
| 650000 | 15004,61 |
| Количество мест в аудиториях | дефицит. | 720 | 1350000 | 1875 |
Из таблицы видно, что ценность второго ресурса выше, чем третьего у 2 >у 3, следовательно в первую очередь следует увеличивать штат преподавателей.
Определим, как скажется на найденном оптимальном решении плата за обучение.
Пусть: C1 - изменяется, а C2=3000
f =C1×x1+3000×x2= const
Представим линию уровня целевой функции в виде прямой с угловым коэффициентом: 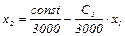
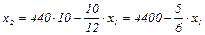 (2)
(2)
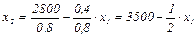 (3)
(3)
Изменение коэффициента С1 может быть таким, чтобы угол наклона линии уровня не вышел за пределы углов наклонов ограничений (2) и (3), только в этом случае найденный план будет оптимальным, т.е
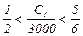 или 1500<C1<2500
или 1500<C1<2500
При изменении платы за обучение студента своей страны, доход изменится следующим образом:
1500×2700+3000×2150<f<2500×2700+3000×2150
10500<f<13200 (тыс. долл.)
Если оплата за обучение студентов своей страны станет меньше 1500 долл., то оптимальной станет вершина А и оптимальный план Х*=(0; 3500), т.е. учить студентов своей страны университету будет невыгодно.
Если С1>2500, то оптимальной станет вершина С и Х*=(4000;733,3).
Рассмотрим случай, когда С1=2000=const, а С2 изменяется. Тогда линия уровня целевой функции в виде прямой с угловым коэффициентом, будет иметь вид: 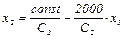
План Х*=(2700; 2150) будет оставаться оптимальным, пока
 или 2400 <С2< 4000
или 2400 <С2< 4000
тогда 2000×2700+2400×2150<f<2000×2700+4000×2150
10560<f<14000 (тыс. долл.)
Если С2 станет меньше 2400, то оптимальной станет вершина С и Х*=(4000;733,3).
Если С2 >4000, то оптимальной станет вершина А и Х*=(0; 4000).
Если С2 =2400, то получим альтернативное решение: оптимальными будут вершины В и С, а любой план, соответствующий любой точке на отрезке ВС будет оптимальным. Коэффициенты этого плана можно получить по формуле:  , где 0 £ a £ 1.
, где 0 £ a £ 1.
Подставив координаты точек В и С получим:
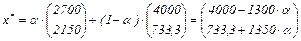
Если С2=4000, то также получим альтернативное решение: оптимальными будут вершины А и В, а любая точка на отрезке АВ будет оптимальным планом: 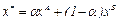 , где 0 £ a £1.
, где 0 £ a £1.
Подставив координаты точек В и С получим
