Критические напряжения изолированного стержня при общей потере устойчивости определяются по формуле Эйлера
, (12.1) где 
-радиус инерции поперечного сечения стержня;
а -длина стержня (рис. 12.3, a);
с - коэффициент, зависящий от характера опирания торцов:
при шарнирном опирании с = 1;
при защемлении с = 4;
для приторцованных концов с = 2.
12.1.2. Критические напряжения, стержня, работающего
совместно с обшивкой.
Если стержень (стрингер) работает не изолированно, а совместно с обшивкой, то общая потеря устойчивости происходит с изгибом его оси в плоскости, перпендикулярной обшивке. Кроме того, на продольный изгиб в этом случае совместно со стрингером, как единое целое, работает и часть обшивки, которая называется присоединенной.
В связи с этим критические напряжения общей потери устойчивости стрингера с присоединённой обшивкой обычно будут выше, чем изолированного.
Момент инерции сечения в формуле (12.1) для этого случая определяется относитель-но центральной оси x '¢- x ' (рис.12.3,б) с учётом площади присоединённой обшивки.
Общаяпотеря устойчивости пояса балочного лонжерона крыла при сжатии невозможна. Скреплённые с поясом стенка и обшивка стесняют изгиб его оси
Рис 12.3. Расчет момента инерции сечения стержня во всех направлениях.
Если критические напряжения, определенные по формуле (12.1), вышепредела пропорциональности, то для дальнейшего расчёта следует использовать формулу
, (12.2)
где n = sb / sкр; sкр - величина, определённая по формуле (12.1).
12.2. КРИТИЧЕСКИЕ НАПРЯЖЕНИЯ МЕСТНОЙ ПОТЕРИ
УСТОЙЧИВОСТИ
При расчёте критических напряжений местной потери устойчивости тонкостенный стержень рассматривается как система прямоугольных пластинок с размерами а, b и d (рис. 12.3, а), соединённых между собой вдоль длинных краёв и по торцам в плоскостях нервюр.
|
|
Haпример, стрингер, представленный на рис. 12.4, состоит из пяти элементов - пластинок, соединённых между собой. Элементы 1 и 5 имеют по три края; шарнирно опертых (два поперечных – на нервюрах и один продольный – на остальной части стрингера) и по одному продольному краю –свободному. Элементы 2, 3, 4 по всем четырем краям оперты.
| Рис. 12.4. Модель стержня |
, (12.3)
где
bi - характерные размеры i -го элемента;
ksi - коэффициент опирания i -го элемента.
В рассмотренном примере величины ks 1 и ks 2 равны:
ks 1 = 0,425 + (b / а)2
ks 2 = ks 3 = ks 4 =4
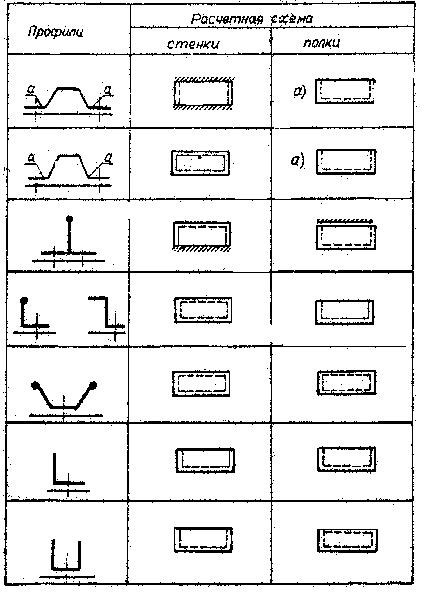
В таблице 12.1 представлены схемы опирания элементов (полок и стенок) для стержней (стрингеров) различной формы поперечного сечения.
На рис. 12.5 рассмотрены примеры определения коэффициентов ks.
рис. 12.5. примеры определения коэффициентов ks
В случае когда s кр. м > s р расчёт критических напряжений проводится с использованием формулы (12.2).
За критические напряжения местной потери устойчивости изо-лированного стержня принимают меньшее из всех напряжений s кр. м.
Для стержней, работающих совместно с обшивкой за величину критического на пряжения, местной потери устойчивости принимают напряжения, определенные по формуле смешения, (12.4)
,
где sкр.мi - критическое напряжение местной потери устойчивости i -го элемента;
f - площадь сечения i -го элемента.
Таблица 12.1
За разрушающее напряжение стрингера принимается наименьшее из критических напряжении общей и местной потери устойчивости.
|
|
sразр =(s кр.мi) min (12.5)
12.3. РАЦИОНАЛЬНЫЕ ФОРМЫ
ПОПЕРЕЧНЫХ СЕЧЕНИЙ
ТОНКОСТЕННЫХ СТЕРЖНЕЙ
Так как тонкостенные стержни могут разрушаться и от местной и от общей потери устойчивости, то размеры поперечных сечений их элементов должны быть такими, чтобы обеспечить, по возможности, наибольшие критические напряжения обеих форм потери устойчивости. желательно, чтобы элементы стержней были равноустойчивы.
Так, например, соотношение размеров b2 и b3 z -образного стрингера
(рис.12.6) можно определить исходя из предпо-ложения, что критические напряжения 1 и 2 элементов одинаковы, т.е
.
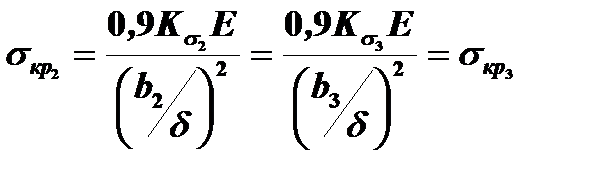Так как 
, а 
, то при постоянной толщине 
.
Рис. 12.6. К расчету критических Наличие отгибов b 3 сильно увеличивает
напряжений элементов стержня коэффициент ks 2 и повышает устойчивость
полки b 2 стрингера. Наивыгоднейшая ширина отгиба b 2 = (0,25…0,3) b 3.
Уменьшение b 3 ведёт к резкому падению устойчивости поддерживаемой стенки b 2, а увеличение b 3, не оказывает влияния на устойчивость полки b 2, но ведёт к значительному ухудшению устойчивости самого отгиба, работающего как пластинка с одним свободные краем.
Для подкрепления стенок прессованных профилей применяют утолщения свободных краёв - бульбы (таблица 12.1), играющие ту же роль, что и отгибы для штампованных.
Утолщение элементов 1, 5 и 3 стрингера, показанного на рисунке. 12.4 (см. первую строку таблицы 2.1), осуществляется какс целью увеличения критических напряжений их местной потери устойчивости, так и для увеличения критических напряжений общей потери устойчивости стрингера, тo же самое следует отметить иу стержней типа тавр и двутавр, полки которых, как правило, выполняются толще стенки. Принятое в них распределение материала по сечению даёт значительное увеличение момента инерции сечения относительно оси, параллельной полкам, а, следовательно, и увеличение критических напряжений общей потери устойчивости.
|
|
ВОПРОСЫ
1. Дайте определение понятия " стержень "?
2. Приведите примеры использования стержней с открытым и замкнутым сечением в авиационных конструкциях.
3. Дайте определение понятия " общая потеря устойчивости стержня".
4. Дайте определение понятия " местная потеря устойчивости стержня".
5. Как определяются критические напряжения изолированного стержня?
6. Как определяются критические напряжениястержня, работающего
совместно с обшивкой?
7. Дайте определение понятия" присоединённая обшивка ".
8. Возможна ли общаяпотеря устойчивости пояса балочного лонжерона крыла при сжатии?
9. Как определяются критические напряжения, если они вышепредела пропорциональности?
10. Как определяются критические напряжения местной потери устойчивости тонкостенного стержня?
11. Опишите применение формулы смешения?
12. Опишите рациональные формы поперечных сечений тонкостенных стержней.
13.