10.5.1. Связь между усилиями и деформациями (σx , σу tху = tух)
нормальные напряжения σxи σу, действующие по граням элементов, эквивалентны изгибающимпогонныммоментамМх и Му(приходящимся на единицу ширины грани).
касательные напряжения tхуи tух, действующие по граням элементов, эквивалентны погонным крутящиммоментамКхуи Кух(приходящимся на единицу ширины грани).
Положительные направления осей системы координат и моментов показаны на рис. 10.7.
По граням элемента, как и в сечениях балки при поперечном нагибе, действуют касательные напряжения tхи ty (см. рис.10.7) от поперечных сил Qxи Qy. При расчётах они ввиду малой величины обычно не определяются.
Тождественность эпюр напряжений для обычной балки и для элемента пластинки позволяет установить связь между напряжениями и моментами
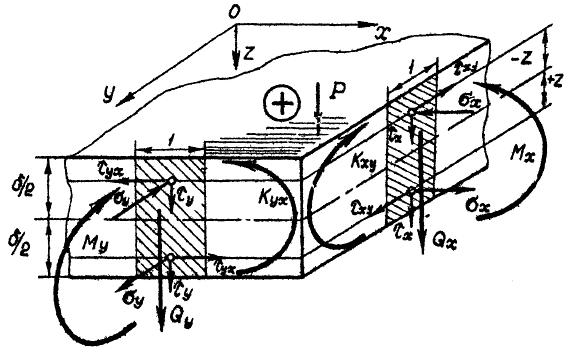
Рис. 10.7 Внутренние силовые факторы и напряжения,
действующие по граням пластины
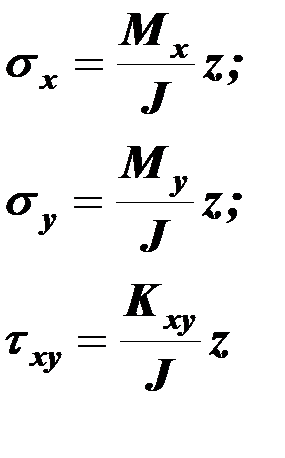(10.2)
Так как напряжения tху иtух определяются для одной в той же точки слоя пластинки, то согласно закону парности они равны, поэтому равны и крутящие моменты Кху= Кyх.
Моменты инерции, как и изгибающие и крутящие моменты, относятся к единице ширины ипоэтому
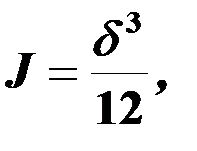
Максимальные величины напряжений:
(10.3)
Деформации слоев пластинки вычисляются на основании закона Гука для плоского напряжённого состояния
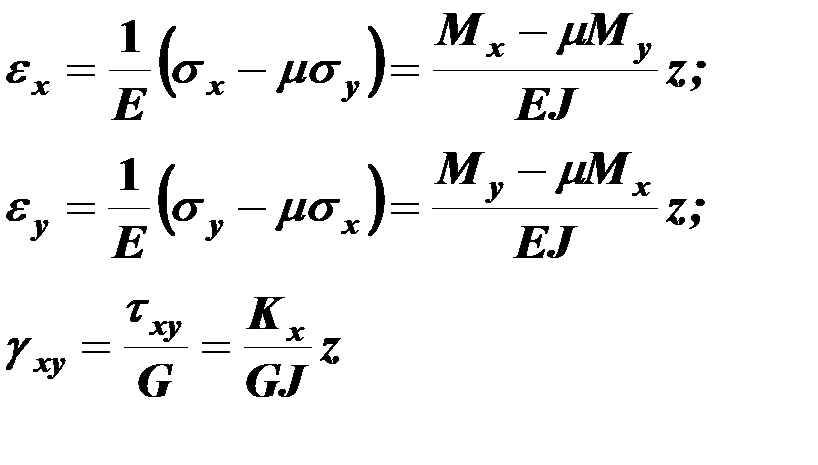(10.4)
Здесь g – модуль сдвига;
γхy – относительный сдвиг.
ВОПРОСЫ
1. Дайте определения понятиям: прямоугольная пластинка, срединная плоскость пластинки, изогнутая срединная поверхность пластинки.
2. Какую нагрузку способна воспринимать пластинка?
3. В каком случае пластинка может воспринимать распределённую нагрузку, направленную перпендикулярно к плоскости пластинки?
4. Можно ли пластинку непосредственно нагружать сосредоточенными силами?
5. Как работает пластинка в составе конструкции?
6. На какие классы делятся пластинки? Кокой принцип этой классификации?
7. Что такое цилиндрический изгиб пластинки?
8. Какие параметры входят в формулу для определения цилиндрической жёсткости пластинки?
УСТОЙЧИВОСТЬ ПЛАСТИНОК
Пластинка является наиболее характерным элементом конструкции самолёта и двигателя. С ней обычно отождествляют элемент обшивки крыла, фюзеляжа, оперения летательного аппарата, стенку лонжерона, нервюры, шпангоута.
Основной особенностью пластинки является её способность воспринима-ть только распределённую нагрузку, действующую главным образом в её плоскости, (рис. 11.1)
Обычная пластинка при действии распределенной поперечной нагрузки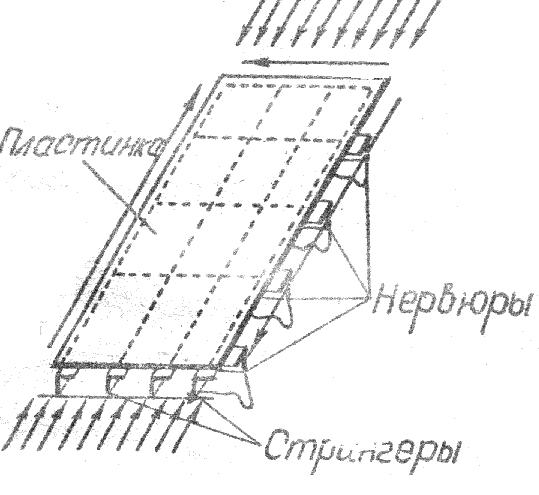 
работает как широкополая; балка сплошного поперечного сечения, но при этом наблюдаются две особенности:
- при изгибе из-за стеснения поперечных деформаций пластинка оказывается несколько более жесткой, чем узкая балка той же площади
цилиндрическая жёсткость - 
выше обычной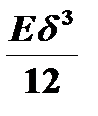 
;
Рис. 11.1. Нагружение пластины - граничные условия для пластинки более разнообразны, так как включают опирание продольных кромок (рис. 11.2), свободных у балки.
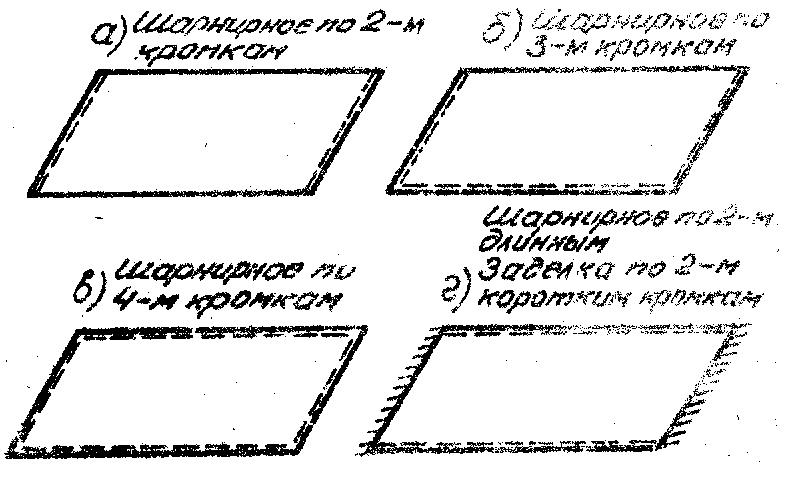Распределённую попе-речную нагрузку пластинка воспринимает плохо и в этом отношении не является рациональным элементом, поскольку работает на изгиб. По этой причине пластинке присущи все недостатки балки сплошного попереч-ного сечения. Обычно применяют пластинки, под-креплённые рёбрами жёсткости (стрингерами, Рис. 10.2. Схемы опирания пластины нервюрами) - панели.
Значительно лучше пластинка работает на восприятие нагрузок, прило-женных в её плоскости (растяжение, сжатие, сдвиг).
При растяжении пластинки разрушаются при достижении в материале напряжений уровня σb(предел прочности при растяжении).
При сжатии и сдвиге пластинки разрушаются из-за потери устойчивости. Нагрузки инапряжения, действующие в момент потери устойчивости, принято называть критическими.
Рассчитать величину указанных напряжений можно с использованием дифференциального уравнения продольно-поперечного изгиба.
