ЦИЛИНДРИЧЕСКИЙ ИЗГИБ ЖЁСТКИХ ПЛАСТИНОК

ПОПЕРЕЧНЫЙ изгиБ ПРЯМОУГОЛЬНЫХ ПЛАСТИНОК

Прямоугольной пластинкой называют тело, имеющее фор­му прямоугольной призмы, высота которой (толщина d) ма­ла по сравнению с другими размерами.

Срединная плоскость пластинки - плоскость, делящая толщину пластинки пополам.

Изогнутой срединной поверхностью пластинки называют поверхность, в которую переходит срединная плоскость при деформации.

Пластинка является наиболее характерным конструктивным элементом авиационных конструкций (элементы обшивки крыла, фюзеляжа, оперения летательного аппарата стенки лонжерона, нервюры, шпангоута).

Рис. 10.1. Нагрузки, действующие на пластинку

Основная особенность пластинки - способность воспринимать только распределённую нагрузку, действующую в её плоскости (рис. 10.1, а). Распределённая нагрузка, направленная перпендикулярно к плоскости пластинки, вы­зывает большие деформации. Поэтому обычно применяются пластинки, подкреплённые рёбрами жесткости (стрингерами, нервюрами;
рис. 10.1, б).

Пластинки нельзя нагружать непосредственно сосредоточенными силами. Сосредоточенная сила, приложенная к пластинке даже в её плоскости, вызывает большие местные деформации и разрушения (рис.10.2, а). В связи с этим пластинки подкрепляют специальными узлами - усиленными стойками, накладками (рис. 10.2, б), которые передают сосредоточенные силы напластинку в виде распределенных потоков погонных касательных усилий q
(рис. 10.2, в).

пластинки - удобный конструк-тивный элемент: они имеют малый Рис. 10.2 Работа пластинок вес, обеспечивают восприятие

аэродинамических сил, защищают внутренние полости летательного аппарата от набегающего потока.

10.1. ОСОБЕННОСТИ НАПРЯЖЕННОГОСОСТОЯНИЯ ПЛАСТИНОК, ИХ КЛАССИФИКАЦИЯ

На рис. 10.3, а показана работа элемента обшивки в виде прямоугольной пластинки при общем изгибе и кручении крыла. вместе со всей конструкцией он воспринимает действие, изгибающего М и крутящего М_к моментов. При этом пластинка несёт нагрузку в своей плоскости. От изгибающего момента в крыле пластинка работает на сжатие (растяжение), от крутящего момента - на сдвиг и по её граням действуют соответственно нормальные σ и касательныеtнапряжения.

Рис. 10.3 Работа элемента обшивки в виде прямоугольной пластинки при общем изгибе и кручении крыла

Так как толщина пластинки мала, то при расчётах общей прочности пренебрегают переменностью напряжений σ и t по её толщине и оперируют обычно не самими напряжениями, а погонными нормальными N = σ × d и погонными касательными q = t × d усилиями. То есть сводят пластинку к срединной поверхности, нагруженной погонными усилиями.

От действия местной поперечной нагрузкир (сил разрежения или давления) этот же элемент обшивки работает дополнительно на местный поперечный изгиб. В крыле он опирается на стрингеры и нервюры

(рис. 10.3, б). В этом случае во взаимно перпендикулярных сечениях элемента возникают переменные по толщине изгибные нормальные и касательные напряжения.

В отдельных случаях при изгибе кроме изгибных напряжений в пластинке могут иметь место значительные растягивающие усилия, которые вызывают нормальные цепные напряжения. Цепные напряжение распределяются по высоте сечения равномерно; они возникают в результате действия на пластинку реакций окантовывающих её рёбер, которые препятствуют сближению краёв пластинки.

Изгибные и цепные напряжения относятся к напряжениям местной прочности.

Полное напряжение в любой точке изогнутой пластинки равно сумме изгибных и цепных напряжений. Величины этих слагаемых зависят от величины прогибов пластинки w (х;у), которые определяются как перемещения точек срединной поверхности в направлении, перпендикулярном к срединной плоскости (рис. 10.4).

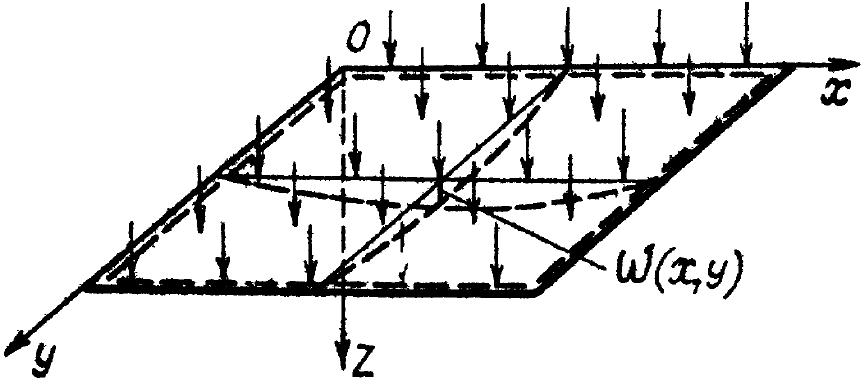
Рис. 10.4 Прогибы пластинки

В зависимости от на­пряжённого состояния, воз­никающего при изгибе, пластинки подразделяются на три класса:

1. Жесткиепластинки, у кото­рых максимальная величи­на прогиба не превосходит 1/4…1/5 толщины d.

У таких пластинок основную роль в напряжённом состоянии играют изгибные напряжения. Цепными напряжениями мож­но пренебречь.

Зависимость между величиной максимального проги­ба жёсткой пластинки и интенсивностью поперечной нагрузки явля­ется линейной.

2. Гибкиепластинки, у которых максимальная величина прогиба находит­ся в пределах (1/4…5) δ.

В этом случае цепные и изгибные на­пряжения соизмеримы.

3. Абсолютно гибкие пластинки, или мембраны, у которых величина про­гибов более, чем в пять раз превосходит толщину пластинки.

У этих пластинок изгибные напряжения малы по сравне­нию с цепными и поперечная нагрузка уравновешивается главным об­разом растягивающими усилиями.

Особенность расчёта напряжённого состояния гибких пластинок и мембран состоит в том, что для них нельзя использовать принцип сложения (независимости) действия сил, так как связь между на­пряжениями и прогибами нелинейная,

ЦИЛИНДРИЧЕСКИЙ ИЗГИБ ЖЁСТКИХ ПЛАСТИНОК

Рассмотрим длинную прямоугольную пластинку (а/в > 3), шарнирно опёртую вдоль длинных сторон на неподвижные опоры (рис. 10.5).

Рис. 10.5Цилиндрический изгиб пластины

Выберем начало координат в угловой точке срединной поверхности пластины. Ось x направим вдоль длинной стороны, ось y - перпендикулярно к ней, а ось Z (прогибов w) - перпендикулярно к срединной плоскости.

пластинка нагружена поперечной нагрузкой р, изменяющейся толь­ко вдоль оси y. Это значит, что все элементарные полоски пластинки, параллельные оси y, нагружены тождественно. В этом случае пластинка будет изгибаться по цилиндрической поверхности собразующими, параллельными оси X. Отклонение от цилиндрической поверхности имеет место только вблизи коротких сторон. Следовательно, прогибы пластинки и напряжения будут функциями лишь одной координаты у. Такая деформация пластинки называется цилиндрическим изгибом.

Мысленно вырежем из пластинки полоски, параллельные оси y шириной, равной единице ирассмотрим их напряжённое идеформи­рованное состояние.

Если бы балки-полоски были изолированными, то их деформация в направлении оси X при изгибе была бы свободной. Поперечные сечения в этом случае принимали бы вид, показанный на рис. 10.5, в. Однако в пластинке эти балки-полоски работают совместно. Слева исправа от выделенной полоски находятся такие же полоски, кото­рые стесняют её деформацию в направлений оси Х (ε_х = 0) ипоперечные сечения остаются прямоугольными (рис. 10.5,б).

Выразим напряжение σ_х через напряжение σ_у. Используем условие стеснения – относительная деформация вдоль оси х равна ε _х = 0. На основании закона Гука для плоского напряжённого состояния имеем

,

Здесь μ – коэффициент Пуассона. Его величина у различных материалов изменяется в пределах от 0 до 0,5.

Отсюда

Определим деформацию продольных волокон пластинки вдоль оси y

Гипотеза прямых нормалей. Точки, лежащие нанормали к срединной плоскости недеформированной пластинки после деформации лежат на нормали к изогнутой поверхности.

Гипотеза плоского напряжённого состояния. При изгибе пластинки слои, параллельные срединной плоскости, не надавливают друг на друга, материал этих слоев находится в плоском напряженном состоянии.

Гипотеза о недеформируемости срединной поверхности. Срединная поверхность при местном изгибе и кручении не испытывает деформации удлинения или сдвига, алишь изгибается как абсолютно гибкая мембрана. В ней при местном изгибе и кручении не возникают напряжений.

Гипотеза обидеальной упругости и изотропности пластинки. Считают, что пластинка обладает одинаковыми свойствами в различных направлениях и её материал подчиняется закону Гука.

В соответствии с принятыми допущениями напряжённое состояние элемента изогнутой жёсткой пластинки будет иметь сле­дующий вид
(рис. 10.6):

- по граням элемента действуют нормальные σ_x, σ_у и ка­сательные t_{ху ,} t_ух напряжения;

- эти напряжения изменяют­ся по толщине пластинки по ли­нейному закону, принимая наи­большие значения у поверхнос­тей и нулевое – в срединном слое;

- так как напряжённое сос­тояние слоев, параллельных срединной плоскости, является плоским, касательные напряжения подчиняются закону парности, то есть для точки слоя А t_ху = t_{ух .}

Рис. 10.6 Напряжённое состояние элемента изогнутой жёсткой пластинки