Задача 17
Определить длину хода плунжера по статической и динамической теориям.
Исходные данные: диаметр плунжера Dпл = 43 мм, диаметр насосных штанг dш = 22 мм, диаметр НКТ - dт = 73 x 5,5 мм, глубина спуска насоса L = 1500 м, длина хода сальникого штока S = 2,1 м, динамический уровень hд = 1450 м, число качаний в минуту n = 15, плотность жидкости ρж = 900 кг/м3, сила сопротивления движению плунжера Рс = 4 кН, буферное давление в выкидной линии - 1,0 МПа, кинематическая вязкость нефти ν = 0,1 см2/с при 80°С.
Решение
Определим параметр Коши по формуле (4.12):
Следовательно, режим откачки находится в области динамических режимов.
Определим среднюю скорость в подъемных трубах:
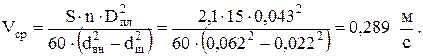
Число Рейнольдса
.
Коэффициент гидравлического сопротивления
.
Потери давления за счет сопротивления потоку жидкости в трубах определим по соотношению
.
Вес столба жидкости над плунжером (формула (4.27))
.
Удлинение штанг (формула (4.26))
.
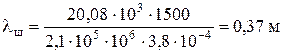Удлинение труб при ходе штанг вниз (формула (4.28))
,
Сжатие штанг за счет силы сопротивления при ходе штанг вниз (формула (4.29))
.
Потери хода за счет изгиба штанг определим по формуле (4.32), так как Рс < 10 кН. Предварительно определим:
Длина хода плунжера при действии статических сил
.
Так как колонна штанг одноступенчатая, а жидкость вязкая, то за расчетную формулу выбираем (4.35). Определим параметр β1, выбирая b = 0,6:
Параметр μ в градусах
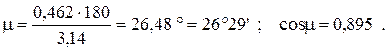
Длина хода плунжера по формуле (4.35)
Варианты заданий к главе 4 даны в табл. 4.6.
Таблица 4.6.
Варианты заданий к главе 4
| Номер варианта | Dт,мм | Dпл, мм | dш, мм | L, м | S, м | hд, м | n, мин-1 | ρж, кг/м3 | Рс, кН | Рб, МПа | ν, см2/с |
| 16/19 | 1,8 | 0,5 | 0,09 | ||||||||
| 19/22 | 2,1 | 0,6 | 0,08 | ||||||||
| 2,5 | 0,7 | 0,1 | |||||||||
| 25/19 | 2,1 | 0,8 | 0,11 | ||||||||
| 5. | 3.0 | 1,0 | 0,12 | ||||||||
| 2,1 | 1,1 | 0,1 | |||||||||
| 19/22 | 2,5 | 1,2 | 0,9 | ||||||||
| 22/19 | 3,0 | 1,3 | 0,02 | ||||||||
| 3,5 | 1,4 | 0,03 | |||||||||
| 3,5 | 1,5 | 0,01 | |||||||||
| 1,8 | 0,4 | 0.02 | |||||||||
| 2,1 | 0,5 | 0,03 | |||||||||
| 8.9 | 19/16 | 2,5 | 0.6 | 0,04 | |||||||
| 22/19 | 3,0 | 0,7 | 0,05 | ||||||||
| 2,5 | 0,8 | 0,06 | |||||||||
| 2,1 | 1,7 | 0.07 | |||||||||
| 2,5 | 0,9 | 0,08 | |||||||||
| 16/19 | 2,5 | 0,8 | 0,10 | ||||||||
| 19/22 | 3,0 | 0,7 | 0,11 | ||||||||
| 3,5 | 1,1 | 0,12 | |||||||||
| 1,8 | 0,8 | 0,1 | |||||||||
| 2,1 | 0,9 | 0,11 | |||||||||
| 2,5 | 1,1 | 0,13 | |||||||||
| 22/25 | 3,5 | 1,2 | 0,12 | ||||||||
| 3,5 | 1,3 | 0,13 |
Расчет производительности и определение коэффициента подачи ШГНУ
4.6.1. Формула производительности по элементарной теории [27|
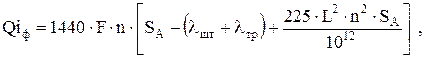(4.37)
где F - площадь поперечного сечения плунжера; n - число двойных ходов в мин; SА - длина хода точки подвеса щтанг; λшт, λтр - удлинение насосных штанг и труб от веса столба жидкости,
, (4.38)
где Рж = hд·ρж·F·g - вес столба жидкости над плунжером; L - глубина подвески насоса; E = 2,1·1011 Н/м2 - модуль упругости стали.
Последний член формулы (4.37) учитывает увеличение длины хода плунжера за счет инерционных сил - δи:
Учитывая массу муфт штанг,
4.6.2. Производительность по элементарной теории А. Н. Адонина [1]
(4.39)
где
- параметр Коши; а - скорость звука в колонне штанг; m - коэффициент, учитывающий влияние инерции столба жидкости.
Для Dпл < 43 мм, m = 1,0;
Dпл = 55 мм, m = 1,5;
Dпл = 68 - 70 мм, m = 2,0;
Dпл=82 мм, m = 4,0;
Dпл = 93мм, m = 3,0;
Dпл = 120мм, m = 4,0.
Формула производительности А. С. Вирновского
(4.40)
где член SА/cosμ, выражающий перемещение плунжера при отсутствии статических удлинений λш и λтр, получен для вынужденных колебаний «свободной» штанги, т. е. штанги без плунжера, при гармоническом законе движения балансира. Отсюда следует, что формула (4.40) применима лишь для насосов малого диаметра (D < 43 мм и μ < 0,785).
Формула (2.39) приемлема для всех диаметров плунжера при μ < 0,55. При больших значениях μ, она дает погрешность около 9% [1].