Длина хода плунжера с учетом действия статических сил
Длина хода плунжера с учетом действия статических сил определяется по формуле [24]:
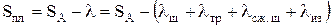, (4.25)
где SА - длина хода точки подвеса штанг (полированного штока); λ - сумма статических деформаций; λш - деформация штанг под действием перепада давления над и под плунжером при ходе вверх,
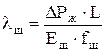. (4.26)
Здесь ΔРж - вес столба жидкости над плунжером,
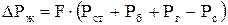, (4.27)
где F - площадь проходного сечения цилиндра; Рст - давление столба жидкости над плунжером; Рб - буферное давление в выкидной линии; Рг - потери давления, обусловленного сопротивлением потоку жидкости в трубах; Рс - давление под плунжером, определяемое глубиной погружения насоса под динамический уровень и сопротивлением потоку жидкости в клапанах насоса и в фильтре, Рс = Рд - Ркл; Еш - модуль упругости материала штанг; L - глубина подвески насоса; fш - площадь поперечного сечения штанг.
Деформация труб при ходе штанг вниз
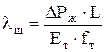. (4.28)
где ΔРж - вес столба жидкости над плунжером; Ет - модуль упругости материала труб; fт - площадь поперечного сечения труб (по металлу).
При ходе штанг вниз на них действует осевая сила, направленная вверх Рс. Эта сила вызвана сопротивлением потоку Жидкости в нагнетательном клапане и трением плунжера о цилиндр. Сила Рс вызывает сжатие и продольный изгиб нижней части колонны штанг.
Если эти силы не уравновешиваются утяжеленным низом штанг, то соответствующая деформация, уменьшающая длину хода плунжера, будет [24]
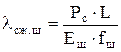; (4.29)
, (4.30)
где Lсж = Рс /qш - длина сжатой части колонны; Rс - радиус спирали, по которой изогнута сжатая часть колонны,
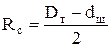; (4.31)
Dт - внутренний диаметр труб; dш - диаметр штанг; I - момент инерции поперечного сечения штанг; qш - вес 1 м длины штанг в жидкости.
Если осевая сила Рс < 10 кН, то можно использовать более простую формулу А. Лубинского для определения λиз:
. (4.32)
Определение длины хода плунжера с учетом статических и динамических сил
Согласно исследованиям А. Н. Адонина граница между статическим и динамическим режимами при откачке жидкости находится в зоне параметра Коши ω·L / а = 0,35 - 0,45, где ω = π·n / 30 - угловая скорость вращения кривошипа; а - скорость звука в штангах (а = 5100 м/с). При двухступенчатой колонне штанг с учетом сопротивлеления движению штанг в вязкой жидкости А. С. Вирновским получена зависимость:
(4.33)
где β1 = b ·L1 / a; b - константа трения, обычно равна 0,2 - 1,0 c-1; μ1 - критерий Коши; fш - площадь сечения штанг;
- гиперболический синус.
Без учета сопротивления движению штанг в вязкой жидкости
(4.34)
Если колонна штанг одноступенчатая, в вязкой жидкости
(4.35)
без учета вязкости (β = 0)
(4.36)
Индексы 1 и 2 соответствуют верхней и нижней ступеням колонны.
Пример расчета длины хода плунжера по статической теории
Задача 16
Определить длину хода плунжера по статической теории.
Исходные данные: диаметр плунжера Dпл = 43 мм, диаметр насосных штанг d = 22 мм, диаметр НКТ dт = 73 х 5,5 мм, глубина спуска насоса L = 1500 м, длина хода сальникого штока S = 2,1 м, динамический уровень hд = 1450 м, число качаний в минуту n = 9, плотность жидкости ρж =900 кг/м3, сила сопротивления движению плунжера Рс = 9 кН, буферное давление в выкидной линии - 1,0 МПа, кинематическая вязкость нефти ν = 0,1 см2/с при 80°С.
Решение
Определим параметр Коши по формуле (4.12):
.
Давление столба жидкости над плунжером
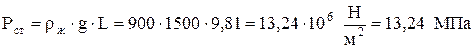
Потери давления за счет сопротивления потоку жидкости в трубах определим по соотношению
,
где средняя скорость в подъемных трубах
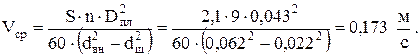
Число Рейнольдса
.
Коэффициент гидравлического сопротивления
.
.
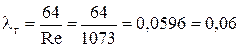Давление под плунжером (сопротивлением клапанов пренебрегаем)
.
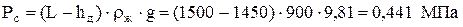Тогда вес столба жидкости над плунжером (формула (4.27))
.
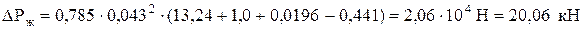Удлинение штанг (формула (4.26))
,
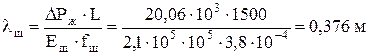где площадь поперечного сечения штанг
.
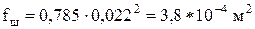Удлинение труб при ходе штанг вниз (формула (4.28))
,
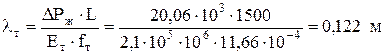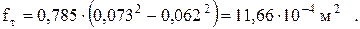
Деформация штанг за счет силы сопротивления при ходе штанг вниз (формула (4.25))
Потери хода за счет изгиба штанг определим по формуле (4.32), так как Рс < 10 кН. Предварительно определим:
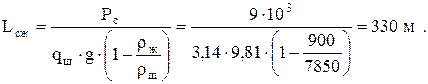
Осевой момент инерции для штанг
.
.
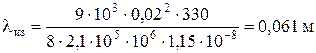Длина хода плунжера при действии статических сил Pпл
.
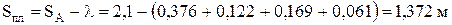