Определение нагрузок производится по различным теориям, которые, в основном, делятся на две группы: статические и динамические. Согласно исследованиям А. Н. Адонина [1] граница между статическим и динамическим режимами откачки находится в интервале (переходная зона) параметра Коши:
,
где а - скорость звука в штангах.
Для одноразмерной колонны а = 4600 м/с, для двухступенчатой а = 4900 м/с; для трехступенчатой а = 5300 м/с. В настоящее время применяют в основном режимы при μ = 0,5 При μ > 0,7 многие формулы просто неприемлемы из-за больших резонансных усилий.
4.2.1. Максимальная нагрузка по статической теории (формула Муравьева И. М.)
, (4.13)
где Рж - вес столба жидкости над плунжером, высотой, равной hд, с учетом буферного давления Рб,
; (4.14)
b - коэффициент облегчения штанг в жидкости,
; (4.15)
m - фактор динамичности,
, (4.16)
где SA - длина хода точки подвеса штанг; n - число качаний в минуту.
Вес штанг в воздухе
.
Минимальная нагрузка будет, очевидно, при начале хода штанг вниз, когда вес жидкости не действует на штанги, а динамический фактор вычитается:
, (4.17)
4.2.2. Определение нагрузок по формулам А. С. Вирновского. Согласно исследованиям А. Н. Адонина [1] они дают наилучшее совпадение с опытными результатами замеров нагрузки:
(4.18)
где Рж - вес столба жидкости высотой hд с учетом буферного давления с площадью, равной Fпл; Р'ж = (Fпл - fшт) ·ρж·g·L - вес столба жидкости в кольцевом пространстве; Fпл, fшт - площадь поперечного сечения плунжера и штанг соответственно; L - глубина спуска насоса; Ршт - вес колонны штанг в воздухе; Р'шт - вес колонны штанг в жидкости.
4.2.3. Формула для минимальной нагрузки получается из предыдущей (4.18), если положить Р'ж = 0, Рж = 0, а кинематические коэффициенты α1 и а1 заменить на аналогичные α2 и а2 при ходе штанг вниз и переменить у двух последних членов знаки на противоположные:
|
|
(4.19)
Здесь SА - длина хода точки подвеса штанг; Ршт - вес колонны штанг в воздухе; Р'шт - вес колонны штанг в жидкости; α1, α2, а1, а2 - кинематические коэффициенты А. С. Вирнов-ского [1,23],
,
где Vmax - действительная максимальная скорость точки подвеса штанг; 1 - при ходе вверх; 2 - при ходе вниз; D, dшт - диаметры насоса и штанг; ω - угловая скорость в 1/с, ω = π·n / 30; λшт - удлинение штанг от веса столба жидкости,
; (4.19')
- коэффициент изменения сечения потока жидкости при переходе от насоса в трубы; Fтр - площадь внутреннего канала труб; fтр - площадь сечения труб по металлу;
- коэффициент отношения площадей.
Если расчет ведется для ступенчатой колонны, то вместо fшт нужно брать
, (4.20)
где ε1, ε2, …, εn - доли ступенчатой колонны штанг, Σεi = 1.
Упрощенные А. Н. Адониным формулы А. С. Вирновского можно использовать для широкого диапазона SА < 5м; n =24 мин-1, D < 93 мм:
;
. (4.21)
4.2.4. Максимальная нагрузка на основе динамической теории по формуле И. А. Чарного
, (4.22)
где tgμ/μ - коэффициент, учитывающий вибрацию штанг:
;
.
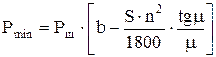4.2.5. Максимальная нагрузка на основе динамической теории по эмпирической формуле А. Н. Адонина
, (4.23)
где m - кинематический коэффициент,
. (4.24)
Здесь Lшат - длина шатуна; k - длина заднего плеча балансира.
Пример расчета нагрузок на головку балансира станка-качалки
Задача 15
Определить максимальную и минимальную нагрузки на головку балансира по различным теориям и сравнить их.
|
|
Дано: глубина подвески насоса L = 1870 м, динамический уровень hд = 1800м, Dпл = 32 мм, dтр = 60мм, диаметры штанг: dш1 = 22 мм, L1 = 560 м (30%); dш2 = 19 мм, L2 = 1310 м (70%); плотность жидкости ρж = 880 кг/м3, станок-качалка СК-12-2,5-4000.
Решение
По формуле (4.12) определим параметр Коши, а = 4900 м/с; α = 1,26 с-1;
.
Режим динамический, следовательно, формулы динамической теории дадут наиболее правильную нагрузку.
1. Статическая теория, формулы (4.13), (4.17).
По формуле (2.14) определим Рж, учитывая, что Рб = 0:
;
.
Для СК-12 SА = 2,5 м, nmax = 12 мин-1. Тогда
.
Вес штанг в воздухе
;
;
.
2. Формулы А. С. Вирновского (4.18) - (4.20).
;
;
;
.
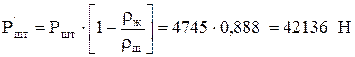Тогда
;
;
;
;
;
.
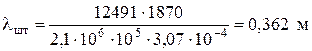Для С К-12-2,5- 4000 при SА = 2,5 м [15]
.
Исходя из вычисленных коэффициентов по формуле (4.18)
По формуле (4.19)
3. Упрощенные формулы А. С. Вирновского (4.21)
;
.
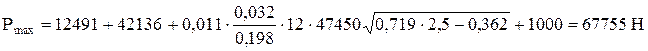4. Формула И. А. Чарного
;
;
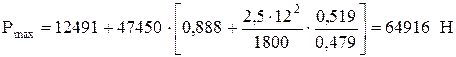5. Формула А. Н. Адонина
;
Таким образом, принимая за основу нагрузку, рассчитанную по формулам А. С. Вирновского, можно сказать, что наиболее близкие значения по Рmax дают формулы А. Н. Адонина (+809) и упрощенная формула А. С. Вирновского (- 3428); по Рmin наиболее близкие значения дают упрощенная формула А. С. Вирновского (+2400 Н) и формула И. М. Муравьева (+3670 Н).
Оценивая трудоемкость расчетов, следует отметить, что для оценочных, приближенных расчетов следует пользоваться формулой для Рmax Муравьева И. М. (4.13) и уточненной автором для Рmin (4.17), а для конструкторских или точных технологических расчетов следует пользоваться формулами А. С. Вирновского или А. Н. Адонина.