СИЛА ИНЕРЦИИ ЗВЕНА, ВРАЩАЮЩЕГОСЯ ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ.

Звено жесткое. Поэтому все его элементарные массы вращаются вокруг оси с одной частотой и одинаковым ускорением ε (рис.3.1.), т.е.

где ω_r(k),ε_r(k) - частота и угловое ускорение k -ой массы звена.

Ускорение k -ой массы звена:

где a_ko - полное ускорение k -ой массы, м/с²,

- ускорение соответственно нормальное и тангенсальное k -ой массы относительно оси вращения, м/с²,

r_k - радиус-вектор, соединяющий k -ую массу с осью вращения звена, м.

Сила инерции k -ой массы:

где - силы инерции k -ой массы соответственно от нормального и тангенциального ускорений.

Выражение 3.6. с учетом 3.2. примет вид:

Это система сил, направленных по r_k от оси вращения, т.е. пересекающихся в оси вращения. Их равнодействующая:

Выражение под интегралом – статический момент. Из курса «Теоретической механики» известно:

где m - масса звена, кг.

r_s - расстояние центра масс от оси вращения, м.

Тогда выражение 3.8. запишется в виде:

Выражение , т.е. нормальное ускорение центра масс звена относительно оси вращения. Поэтому окончательно:

Она направлена вдоль вектора r_s от оси вращения.

Теперь рассмотрим выражение 3.7. – тангенциальную составляющую силы инерции элементарной массы. С учетом 3.4. оно примет вид:

Рисунок 3.1- Силы инерции вращающегося звена

Силы перпендикулярны к соответствующим r_k, т.е. представляют систему произвольно расположенных сил в плоскости. После преобразований, аналогичных предыдущим, получим:

Направление ее противоположно вектору ускорения , т.е. перпендикулярно радиусу-вектору

Точку приложения можно найти из условия равенства ее момента относительно оси вращения звена сумме моментов элементарных сил инерции элементарных масс относительно той же оси:

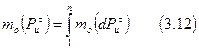
Левая часть: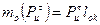

где l_ok - искомое расстояние точки приложения P от оси вращения звена, м.

Подставив сюда значение из 3.11, получим:

Преобразуем правую часть 3.12:

Выражение под интегралом является моментом инерции относительно оси, проходящей через центр вращения и перпендикулярно к плоскости движения. Принято называть сокращенно – момент инерции звена относительно оси. Он характеризует распределенность массы – форму звена и является показателем инертности, его энергоемкости, обозначается:

Выражение 3.14 при этом примет вид:

Тогда искомое расстояние l_ok с учетом 3.13 определяется:

Перенесем в найденную точку k и силу инерции звена от нормального ускорения. Равнодействующая и :

Таким образом, сила инерции звена, совершающего вращательное движение, равна произведению его массы на полное ускорение центра масс. Приложена она в точке, отстоящей от оси вращения на расстоянии l_ok и направлена противополож- но ускорению центра масс.

Обычно известен J_s - момент инерции звена относительно масс. Из теоретической механики известно:

Точку приложения силы инерции звена можно определ- ить с учетом 3.15:

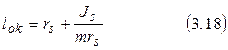
Рисунок 3.2 - К физическому смыслу

Эту точку назы- вают центром качания или еще центром удара. Последнее имеет вполне определенный физический смысл и учитывается при проектировании машин. Пусть звено 1, вращается вокруг А, падает и ударяет в точку В, расстояние которой от оси А можно изменять. При опора А испытывает удар вниз, а при - вверх. Когда , шарнир А вовсе не испытывает удара – динамической нагрузки. Если звено совершает процесс дробления какого-либо материала, то в этом случае вся сила его инерции расходуется полезно.